Longest Common Subsequence

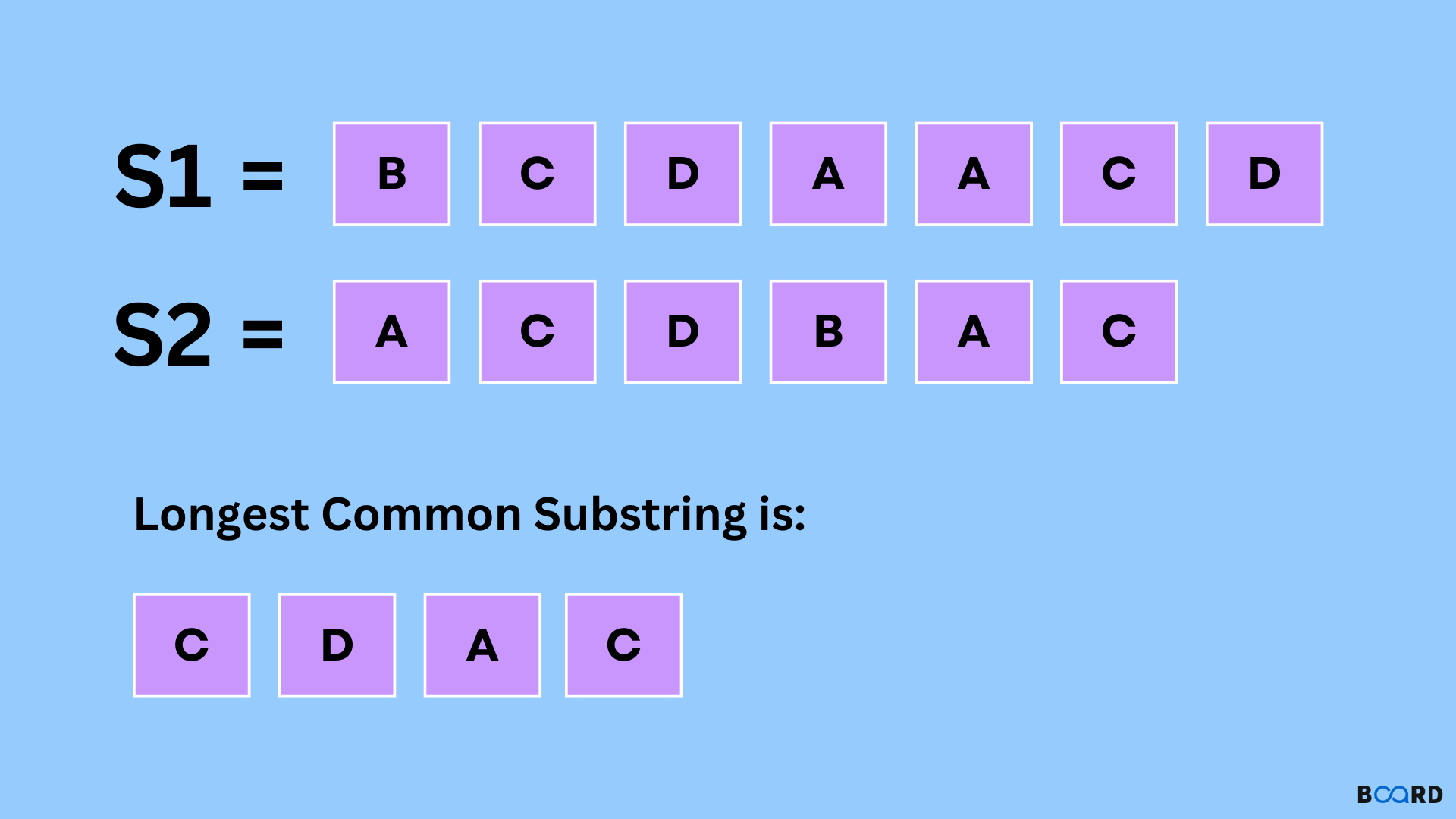
개요

순환식

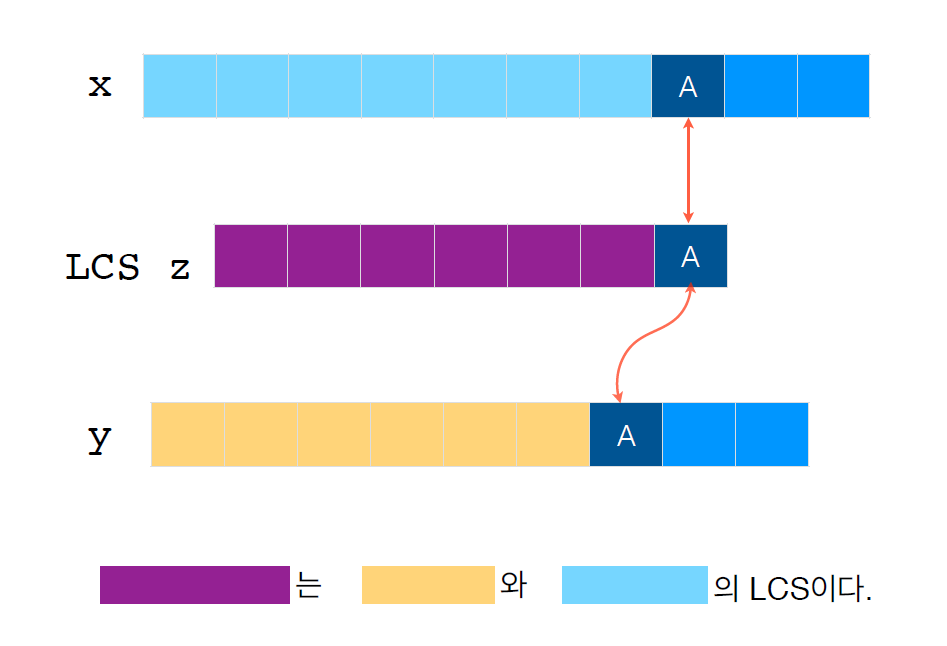
f(i,j)를 x(x1, x2, ... , xi)와 y(y1, y2, ... yj)의 LCS 길이라고 하자.

1. xi = yi라면 f(i,j) = f(i-1, j-1) + 1이다.

2. xi != yi라면 xi와 yj둘 중 하나를 제거해야 하므로 f(i,j) = max{f(i-1, j), f(i, j-1)}이다.

3. i와 j가 줄어들며 0이될 때가 Base Case이다.

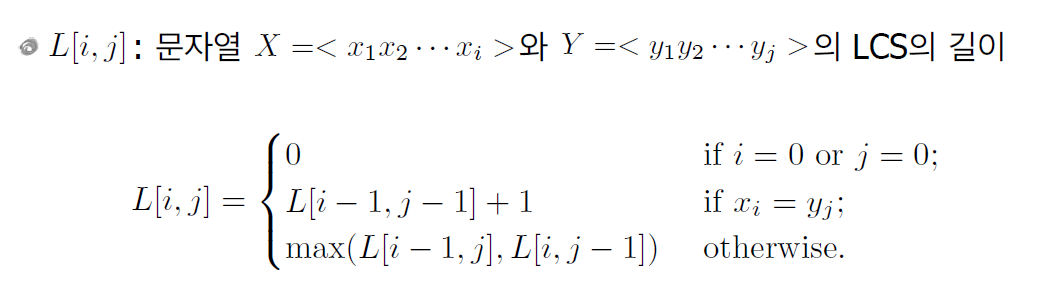
Dynamic Programming

int LCS(char* X, char* Y) {
	for (int i = 0; i <= strlen(X); i++)
		m[i][0] = 0;
	for (int j = 0; j <= strlen(Y); j++)
		m[0][j] = 0;

	for (int i = 1; i <= strlen(X); i++) {
		for (int j = 1; j <= strlen(Y); j++) {
			if (X[i - 1] == Y[j - 1]) {
				m[i][j] = m[i - 1][j - 1] + 1;
				printf("(%c %c) ", X[i - 1], Y[j - 1]);
			}
			else
				m[i][j] = max(m[i - 1][j], m[i][j - 1]);
		}
	}
	return m[strlen(X)][strlen(Y)];
}

string을 indexing할 때 -1 해주는 것을 주의한다.

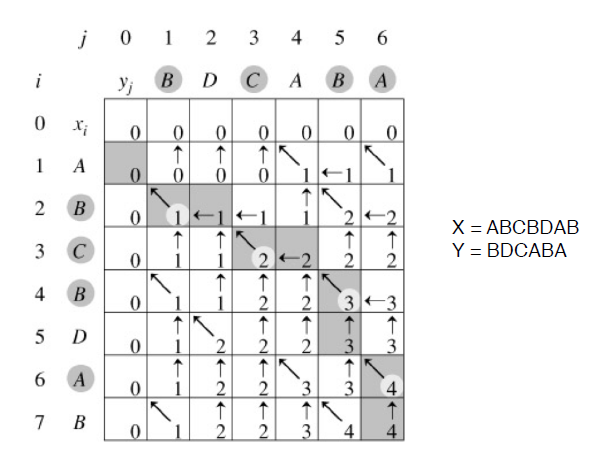
다음의 테이블이 완성된다.

char* LCS_print(char* X, char* Y) {
	int i = strlen(X), j = strlen(Y);
	int index = m[i][j];
	char* s = (char*)malloc(sizeof(char) * (index + 1));

	while (i > 0 && j > 0) {
		if (X[i - 1] == Y[j - 1]) {
			s[index - 1] = X[i - 1];
			i--;
			j--;
			index--;
		}
		else if (m[i - 1][j] > m[i][j - 1])
			i--;
		else
			j--;
	}

	s[m[strlen(X)][strlen(Y)]] = '\0';
	return s;
}