Q. n과 k를 입력받아 nCk의 값을 계산하는 프로그램을 작성하시오.
개요
nCk는 n개중에 k개를 (순서와 상관없이) 선택하는 경우의 수를 의미한다.
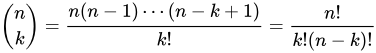
이항계수(조합)의 값을 구하는 프로그램을 만들 때, n!는 아주 큰 수가 될 수 있기 때문에 점화식(순환식)을 이용한다.
전체 집합에서 특정 원소(A)를 포함하는 경우와 포함하지 않는 경우의 합으로 나타낼 수 있다.
- A를 포함하는 경우: C(n-1, k-1)
- A를 포함하지 않는 경우: C(n-1, k)
따라서 C(n, k) = C(n-1, k) + C(n-1, k-1)이 성립한다.
Recursion
이항계수의 전제조건은 n >= k, n > 0, k >= 0이다.
Recursive Case에서 k의 값은 계속 감소하므로 k가 n과 같아질 경우와, k가 0이 될 경우를 Base Case로 설정해주어야 한다.
int bc_r(int n, int k) {
if (n == k || k == 0)
return 1;
return bc_r(n - 1 , k) + bc_r(n - 1, k - 1);
}하지만 Recursion을 이용하면 다음과 같은 중복 계산이 발생하므로 효율적이지 못한다.
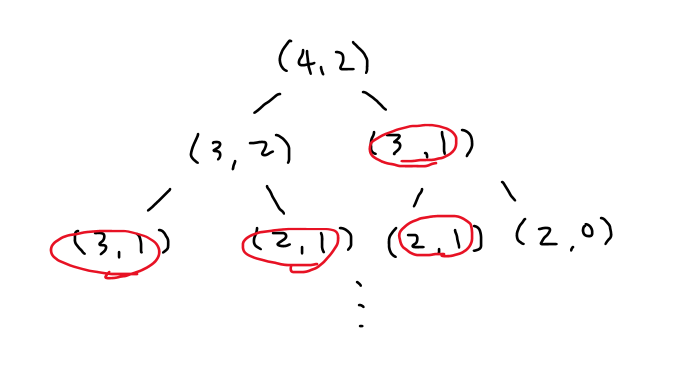
Memoization
Memoization은 Recursion을 이용해 답을 구하기 위해 필요한 계산의 결과들을 이차원 배열에 저장한다.
결과를 구하기 위해 필요한 계산만 수행하는 Top-down 방식이다.
예를 들어 C(3, 1)을 구하기 위해서 C(2, 1), C(1, 1)만을 이차원 배열에 저장한다.
Recursion을 이용하기 때문에 overhead가 수반될 수 있다.
int bc_m(int n, int k) {
if (n == k || k == 0)
return 1;
if (m[n][k] != -1)
return m[n][k];
m[n][k] = bc_m(n - 1, k, m) + bc_m(n - 1, k - 1, m);
return m[n][k];
}Dynamic Programming
Dynamic Programming은 반복문을 이용해 Base Case부터 계산의 결과들을 이차원 배열에 저장한다.
순환식의 우변이 먼저 배열에 저장되는 Bottom-up 방식이 되도록 계산 순서를 고려해야 한다.
int bc_d(int n, int k) {
if (d[n][k] != -1)
return d[n][k];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= k && j <= i; j++) {
if (i == j || j == 0)
d[i][j] = 1;
else {
d[i][j] = d[i - 1][j] + d[i - 1][j - 1];
}
}
}
return d[n][k];
}

