Red-Black Tree 예쁘다.

1. 배경

• BST의 모든 연산은 높이 (h)와 관련있다.

• n개의 데이터를 무작위 (random permutation)으로 BST에 삽입 할 경우, 높이는 평균적으로 O(nlogn)이다.

• 현실의 데이터는 무작위하지 않다. (데이터가 이미 정렬 된 경우 BST의 높이는 n이 된다.)

Red-Black Tree는 어떤 경우에도 Tree의 Balance를 무너지지 않게 한다.

2. 조건

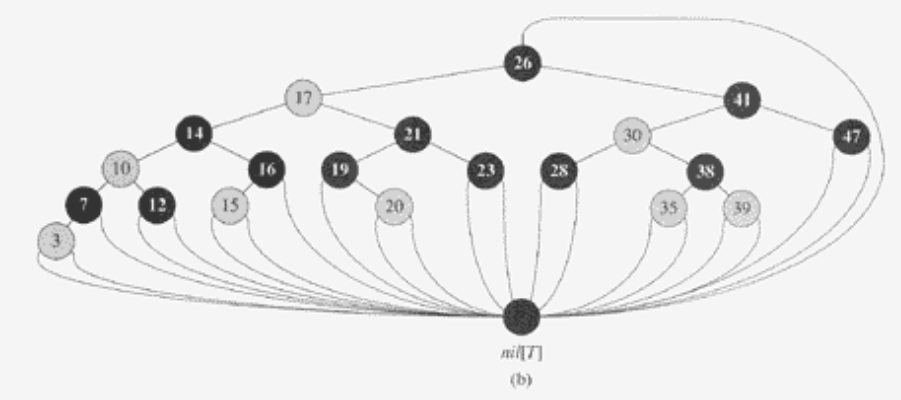
• RBT의 노드는 internal node (데이터를 가지고 있는 노드)와 leaf node (NULL 노드)로 나누어진다.

Red-Black Property

1. 모든 노드는 Red 혹은 Black이다.

2. Root는 Black Node이다.

3. 모든 Leaf (Null node)는 Black이다.

4. Red 노드의 자식노드는 Black이다. (Red 노드는 연속하지 않는다.)

5. 모든 노드에 대해 Leaf (Null)노드에 이르는 경로의 Black 노드의 개수는 같다.

• 높이 (Height)란 자신으로부터 NULL까지 가는 최대 Edge의 개수를 말한다.

• 블랙 높이 (Black height)란 x노드로부터 NULL까지 가는 자신을 포함하지 않은 블랙 노드의 개수를 말한다.

RBT의 root 노드의 높이가 O(nlogn)가 되는 이유 증명

1. 높이가 h인 노드의 bh는 bh >= h / 2이다.
: Red 노드가 연속 될 수 없으므로

2. root를 x로 하는 임의의 부트리의 내부 노드 개수 n은 n >= 2^(bh(x))-1이다. (수학적 귀납법)
: bh(x) = 1일 때 식을 만족한다.
: x가 두 black 노드를 자식으로 가질 때 가정에 의하여 각 자식 노드의 내부 노드 개수 nc는 nc >= 2^(bh(x)-1)-1이다.
: 따라서 x의 내부 노드 개수 n은 n = nc + nc + 1이므로 n >= 2*(2^(bh(x)-1)-1)+1 = 2^(bh(x))-1이다.

3. n >= 2^(bh(x))-1 = 2^(h(x)/2)-1이므로 2^(h(x)/2) <= n+1이다. 따라서 h(x) <= 2log(n+1)이므로 x를 root로 하는 tree의 높이는 O(nlogn)이다.

3. 구현

Red-Black Tree는 다음과 같이 NIL node를 사용해서 구현하는 것이 편리하다.

typedef struct rbtree {
	node* root;
	node* NIL;
}rbtree;

node가 NIL node와 같다면 그 node는 leaf node이다.
이 때 NULL과 비교하면 안되는데, 따라서 모든 함수에 rbtree* 타입의 매개변수가 필요하다. (특히 inorder traversal과 같은 재귀 함수)

1) Insertion

• 새로운 노드는 모두 Red다.

• 새로운 노드의 부모 노드가 Red일 때 Red-Red 문제가 발생한다.

2) Deletion

• 삭제할 노드가 Black일 때 문제가 발생한다.

Insertion과 Deletion은 간단히 말해 Red-Black property를 해치는 모든 경우의 수를 나눠서 문제 node의 색깔을 수정한다.

3) 코드

#include <stdio.h>
#include <stdlib.h>

enum Color {B, R};

char get_color(enum Color color) {
	switch (color) {
	case B: return 'B';
	case R: return 'R';
	}
}

typedef struct node {
	struct node* parent;
	struct node* left;
	struct node* right;
	int data;
	enum Color color;
}node;

typedef struct rbtree {
	node* root;
	node* NIL;
}rbtree;

node* new_node(int data) {
	node* n = (node*)malloc(sizeof(node));
	
	n->parent = NULL;
	n->left = NULL;
	n->right = NULL;
	n->data = data;
	n->color = R;

	return n;
}

rbtree* new_rbtree() {
	rbtree* t = (rbtree*)malloc(sizeof(rbtree));
	node* nil_node = (node*)malloc(sizeof(node));
	
	nil_node->parent = NULL;
	nil_node->left = NULL;
	nil_node->right = NULL;
	nil_node->data = -1;
	nil_node->color = B;
	t->NIL = nil_node;
	t->root = t->NIL;

	return t;
}

void left_rotation(rbtree* t, node* x) {
	node* y = x->right;
	
	x->right = y->left;

	if (y->left != t->NIL)
		y->left->parent = x;

	y->parent = x->parent;

	if (x->parent == t->NIL)
		t->root = y;
	else if (x == x->parent->left)
		x->parent->left = y;
	else
		x->parent->right = y;

	y->left = x;
	x->parent = y;
}

void right_rotation(rbtree* t, node* x) {
	node* y = x->left;

	x->left = y->right;

	if (y->right != t->NIL)
		y->right->parent = x;

	y->parent = x->parent;

	if (x->parent == t->NIL)
		t->root = y;
	else if (x == x->parent->left)
		x->parent->left = y;
	else
		x->parent->right = y;

	y->right = x;
	x->parent = y;
}

void insertion_fixup(rbtree* t, node* z) {
	while (z->parent->color == R) {
		// Case 1, 2, 3
		if (z->parent == z->parent->parent->left) {
			node* y = z->parent->parent->right;

			// Case 1
			if (y->color == R) {
				z->parent->color = B;
				y->color = B;
				z->parent->parent->color = R;
				z = z->parent->parent;
			}
			// Case 2, 3
			else {
				// Case 2
				if (z == z->parent->right) {
					z = z->parent;
					left_rotation(t, z);
				}
				// Case 3
				z->parent = B;
				z->parent->parent->color = R;
				right_rotation(t, z->parent->parent);
			}
		}
		// Case 4, 5, 6
		else {
			node* y = z->parent->parent->left;

			// Case 4
			if (y->color == R) {
				z->parent->color = B;
				y->color = B;
				z->parent->parent->color = R;
				z = z->parent->parent;
			}
			// Case 5, 6
			else {
				// Case 5
				if (z == z->parent->left) {
					z = z->parent;
					right_rotation(t, z);
				}
				// Case 6
				z->parent->color = B;
				z->parent->parent->color = R;
				left_rotation(t, z->parent->parent);
			}
		}
	}
	t->root->color = B;
}

void insertion(rbtree* t, node* z) {
	node* y = t->NIL;
	node* x = t->root;

	while (x != t->NIL) {
		y = x;
		if (z->data < x->data)
			x = x->left;
		else 
			x = x->right;
	}

	z->parent = y;

	if (y == t->NIL)
		t->root = z;
	else if (z->data < y->data)
		y->left = z;
	else
		y->right = z;

	z->left = t->NIL;
	z->right = t->NIL;
	z->color = R;

	insertion_fixup(t, z);
}

node* rbtree_find(rbtree* t, int k) {
	node* x = t->root;
	
	while (x != t->NIL) {
		if (k == x->data)
			return x;
		else if (k < x->data)
			x = x->left;
		else
			x = x->right;
	}
	if (x == t->NIL)
		return NULL;
}

node* rbtree_min(rbtree* t, node* x) {
	while (x->left != t->NIL)
		x = x->left;
	return x;
}

node* successor(rbtree* t, node* x) {
	if (x->right != t->NIL)
		return rbtree_min(t, x->right);
	else {
		node* y = x->parent;

		// Find the first left child of parent above
		while (y != t->NIL && x == y->right) {
			x = y;
			y = y->parent;
		}
		return y;
	}
}

void deletion_fixup(rbtree* t, node* x) {
	while (x != t->root && x->color == B) {
		node* w; // sibling of x

		// Case 1, 2, 3, 4
		if (x == x->parent->left) {
			w = x->parent->right;
			
			// Case 1
			if (w->color == R) {
				w->color = B;
				x->parent->color = R;
				left_rotation(t, x->parent);
				w = x->parent->right;
			}
			// Case 2
			if (w->left->color == B && w->right->color == B) {
				w->color = R;
				x = x->parent;
			}
			// Case 3, 4
			else if (w->right->color == B) {
				w->left->color = B;
				w->color = R;
				right_rotation(t, w);
				w = x->parent->right;
			}
			// Case 4
			w->color = x->parent->color;
			x->parent->color = B;
			w->right->color = B;
			left_rotation(t, x->parent);
			x = t->root; // in order to escape from the loop
		}
		// Case 5, 6, 7, 8
		else {
			w = x->parent->left;

			// Case 5
			if (w->color == R) {
				w->color = B;
				x->parent->color = R;
				right_rotation(t, x->parent);
				w = x->parent->left;
			}
			// Case 2
			if (w->left->color == B && w->right->color == B) {
				w->color = R;
				x = x->parent;
			}
			// Case 3, 4
			else if (w->left->color == B) {
				w->right->color = B;
				w->color = R;
				left_rotation(t, w);
				w = x->parent->left;
			}
			// Case 4
			w->color = x->parent->color;
			x->parent->color = B;
			w->left->color = B;
			right_rotation(t, x->parent);
			x = t->root; // in order to escape from the loop
		}
	}
	x->color = B;
}

void deletion(rbtree* t, int k) {
	node* z = rbtree_find(t, k);
	node* y; // actual node to delete
	node* x; // node to transplant

	// z has 0 or 1 child
	if (z->left == t->NIL || z->right == t->NIL)
		y = z;
	else
		y = successor(t, z);

	// Transplanting
	if (y->left != t->NIL)
		x = y->left;
	else
		x = y->right;
	x->parent = y->parent;

	if (y->parent == t->NIL)
		t->root = x;
	else if (y = y->parent->left)
		y->parent->left = x;
	else
		y->parent->right = x;

	// y is successor of z
	if (y != z)
		z->data = y->data;

	if (y->color == B)
		deletion_fixup(t, x);

	free(y);
}

/*
* Returns the height from the root node to the deepest leaf node
* The height of the root node is 1
*/
int height(rbtree* t, node* root) {
	if (root == t->NIL) {
		return 0;
	}

	int lh = height(t, root->left);
	int rh = height(t, root->right);

	if (lh > rh)
		return 1 + lh;
	else
		return 1 + rh;
}

void print_in_order(rbtree* t, node* root) {
	if (root == t->NIL) {
		return;
	}

	print_in_order(t, root->left);
	printf("%d\n", root->data);
	print_in_order(t, root->right);
}

void padding(char ch, int n) {
	for (int i = 0; i < n; i++)
		putchar(ch);
}

void print_tree(rbtree* t, node* root, int level) {
	if (root == t->NIL) {
		return;
	}
	else {
		print_tree(t, root->right, level + 1);
		padding('\t', level);
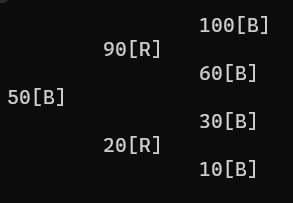
		printf("%d[%c]\n", root->data, get_color(root->color));
		print_tree(t, root->left, level + 1);
	}
}

int main() {
	rbtree* t = new_rbtree();

	node* a, * b, * c, * d, * e, * f, *g, *h;

	a = new_node(10);
	b = new_node(20);
	c = new_node(30);
	d = new_node(100);
	e = new_node(90);
	f = new_node(40);
	g = new_node(50);
	h = new_node(60);

	insertion(t, a);
	insertion(t, b);
	insertion(t, c);
	insertion(t, d);
	insertion(t, e);
	insertion(t, f);
	insertion(t, g);
	insertion(t, h);

	deletion(t, 40);

	print_tree(t, t->root, 0);
}