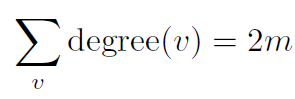Graph

1. 그래프의 표현

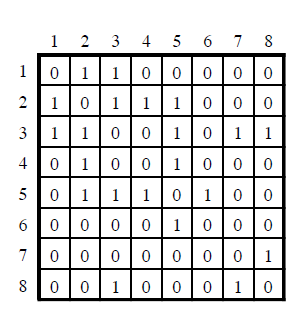
1. Adjacency Matrix

• 저장 공간: O(n^2)

• 노드 v에 인접한 노드 찾기: O(n)

• 에지 (u,v) 찾기: O(1)

2.Adjacency List

무방향 그래프이므로 노드의 개수는 2m이다.

m은 에지의 개수이고 최악의 경우 n(n-1)/2 (대각선의 개수)가 될 수 있다.

degree(v)는 노드 v의 인접 노드 개수이다.

• 저장 공간: O(n + m)

• 노드 v에 인접한 노드 찾기: O(degree(v))

• 에지 (u,v) 찾기: O(degree(u))

2. 그래프 순회

1. BFS

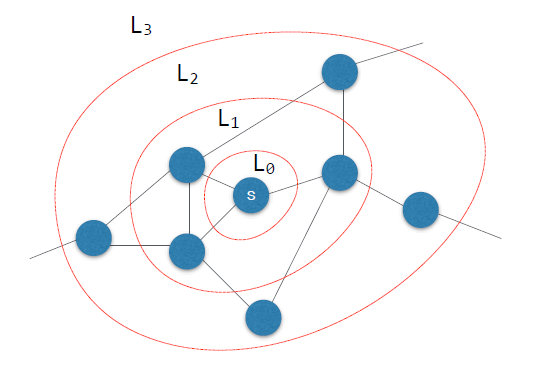
Queue를 이용한다.

출발 노드 s로부터 동심원 형태로 순회한다.

출발 노드로 부터 어떤 노드까지의 최단 거리와 경로를 구할 수 있다.

• Psuedo Code

• 시간 복잡도

: Queue의 길이는 총 노드의 개수이므로 while문은 n번 돈다.

: for문은 각 노드 v에 대해 degree(v)번 도므로 총 2m (모든 에지의 개수)의 시간이 든다.

: 따라서 O(n + m)이다.

: 인접 행렬을 사용했을 때 인접 노드 탐색에 n이 걸리므로 시간 복잡도는 O(n^2)이 된다.

• BFS Tree

: 모든 노드들을 자신의 Predecessor (π)와 연결하면 트리가 만들어진다.

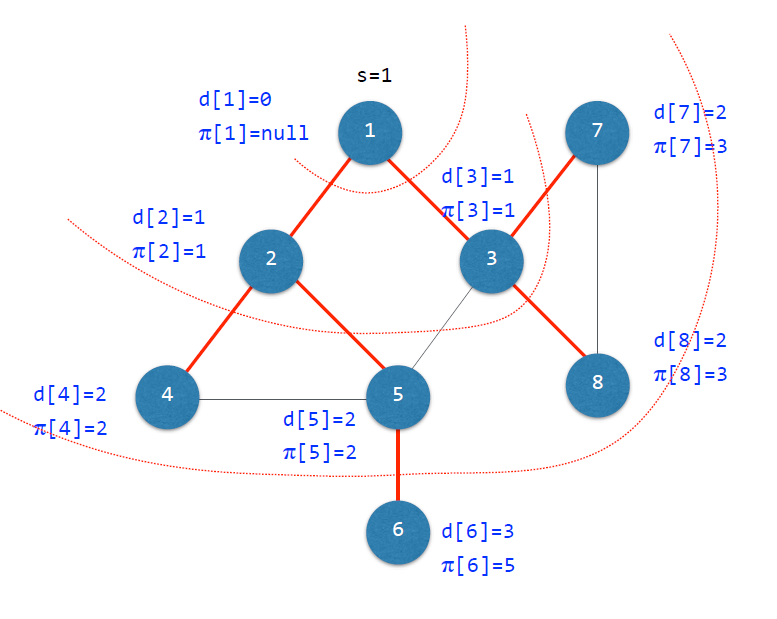
2. BFS를 이용한 경로 출력

3. DFS

: Recursion을 이용해 unvisited 상태인 인접 노드를 우선 탐색하고, 길이 막히면 이전의 상태로 돌아간다. (caller 함수로 돌아간다.)

3. DAG (Directed Acyclic Graph)

: 방향 비순환 그래프 (작업의 우선순위)

1. 위상 정렬

: DAG 노드들의 순서화 (우선순위가 망가지면 안된다.)

• 알고리즘 2