응용수학 복습 1

1. 속력과 속도

• 속력
  : 단위시간당 이동한 거리
  : 스칼라 값

• 속도
  : 단위시간당 변한 출발점과의 거리 및 방향
  : 벡터 값

2. 중간값 정리

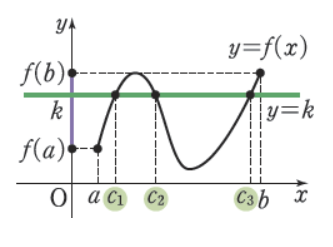
: f(x)가 폐구간 [a,b]에서 연속이고 f(a) != f(b)이면, f(a) < k < f(b)인 임의의 값 k에 대하여 f(c) = k인 c가 (a,b)에 적어도 하나 존재한다.

3. 미분법

• 합성함수
  : {f(g(x))}' = f'(g(x)) * g'(x)

• 음함수

  • 음함수란: f(x,y) = 0 꼴의 식
  • y^3 = {g(x)}^3라 두고 x에 대해 미분하면 합성함수의 미분법에 의해 3{g(x)}^2 dg(x) / dx, 즉 3y^2 dy / dx가 된다.
  • dy/dx를 제외한 부분을 우변으로 넘겨 정리하면 된다.

4. 중간값 정리의 활용

• 롤의 정리

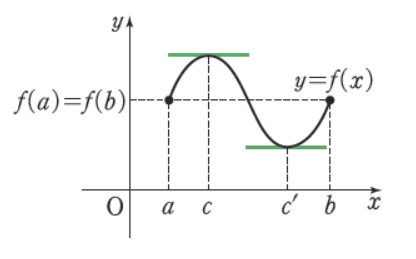
f(x)가 [a,b]에서 연속이고 (a,b)에서 미분 가능하면, f(a) = f(b)일 때 f'(c) = 0, 즉 기울기가 0인 점 c가 (a,b)에 적어도 하나 존재한다.

• 평균값 정리

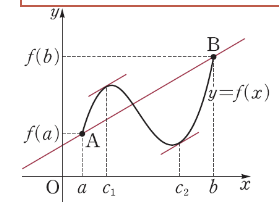
롤의 정리와 마찬가지로 평균 기울기 f'(c) = f(b) - f(a) / b - a 인 점 c가 (a,b)에 적어도 하나 존재한다.

5. 로피탈 정리

주어진 함수의 극한이 0/0 이거나 ∞/∞ 꼴인 경우, 분자 분모를 각각 미분한 후에 그 극한을 구해도 결과가 같다.

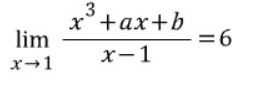
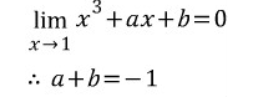
6. 테일러 정리

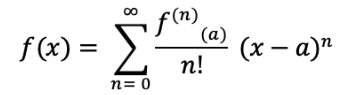
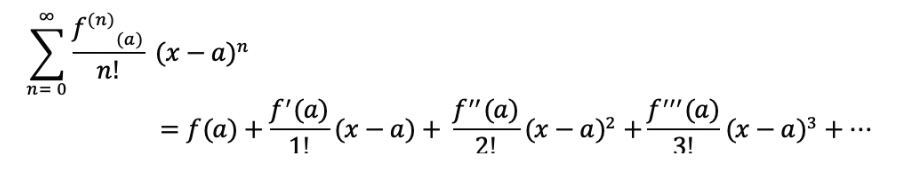
: 다항함수가 아닌 함수들을 다항함수로 표현하기 위함

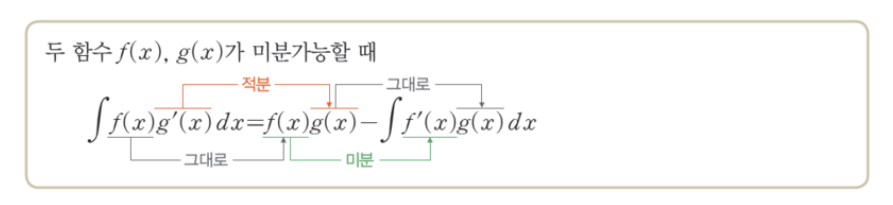
7. 적분법

• 치환적분
  : f'(x)가 3x^2sin(x^3)처럼 합성함수의 미분의 형태일 때 f'(x)를 적분한 결과는 -cos(x^3)이 된다.

• 부분적분
  : f'(x)가 치환적분이 가능한 형태가 아닌 두 함수의 곱으로 나타나 있을 때 사용한다.
  : 함수의 곱을 미분이 쉬운 함수와 적분이 쉬운 함수로 나눈다.