응용수학 복습2

1. 전치행렬

• 형태
  

• 기본 성질

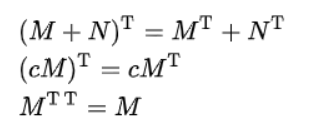
• 임의의 행렬과 그 행렬의 전치 행렬의 행렬식은 같다.

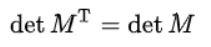
• 임의의 행열이 가역하면 그 전치행렬도 가역하다.

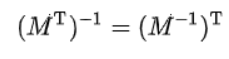
2. 선형 독립과 선형 종속

• 행렬의 한 벡터가 다른 벡터들의 선형 결합으로 표현될 수 있으면 선형 종속이고 그렇지 않으면 선형 독립이다.

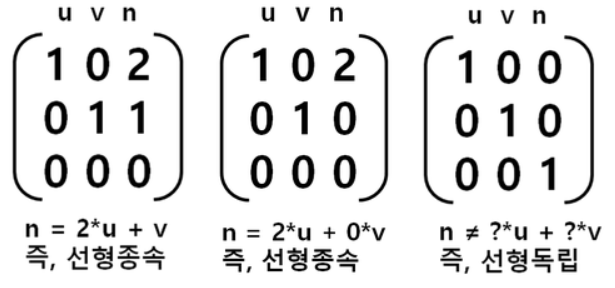
• 행렬 X가 역행렬이 존재하면 영벡터가 유일한 해이므로 X는 선형 독립

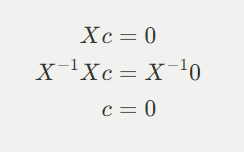
• 행렬 X가 역행렬지 존재하지 않으면 영벡터 외의 해가 있으므로 X는 선형 종속

3. 행렬의 랭크 (계수)

• 행공간과 열공간의 차원을 말하며 행 계수와 열 계수는 항상 같다.

• 독립인 벡터의 개수를 의미한다.

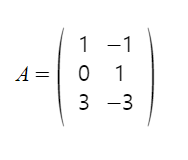
• 위 행렬에서 열 벡터 y1 = (1, 0, 3)과 y2 = (-1, 1, -3)은 서로 독립이다. 따라서 열 계수는 2이다.
• 독립인 행 벡터의 개수는 (1, -1)과 (0, 1)로 2개이다.