12-1 공간으로 시간을 살 수 있나요?
12-2 해싱
12-3 백트래킹
12-1 공간으로 시간을 살 수 있나요?
알고리즘 설계에서의 시간-공간 트레이드오프
- 시간과 공간의 효율성은 항상 서로 충돌하는 요소
- 시간 효율성이 더 중요하게 인식되기 때문에 공간을 희생해 많은 메모리를 사용하여 처리시간을 줄이려는 다양한 전략들이 개발되고 있음
" → 공간으로 시간을 살 수 있음
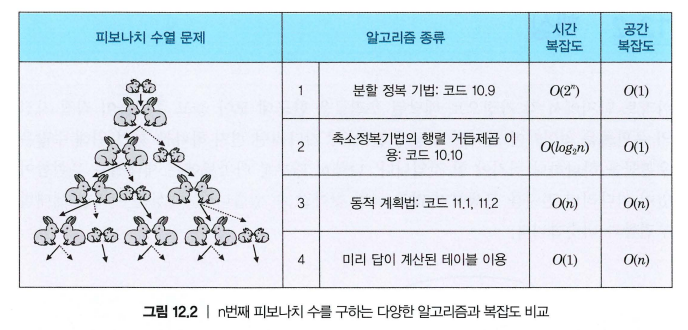
피보나치 수열 예시
- 재귀 방식: 계산을 반복하여 매우 느림
- 동적 계획법: 중복 계산을 피함
- 테이블 미리 저장: 최단 시간에 결과 반환
| 방법 | 시간 복잡도 | 공간 복잡도 |
|---|---|---|
| 재귀 (분할정복) | O(2ⁿ) | O(1) |
| 행렬 거듭제곱 | O(log n) | O(1) |
| 동적 계획법 (DP) | O(n) | O(n) |
| 테이블 미리 계산 후 사용 | O(1) | O(n) |
현실 속 활용 사례
- 다양한 알고리즘에서 공간을 써서 시간 효율을 높이는 방식이 자주 쓰임
- 주요 예시
- 기수 정렬 (Radix Sort)
- 미리 준비한 버킷을 활용해 데이터를 정렬
- 거의 O(n)에 가까운 성능
- 문자열 매칭 (KMP 등)
- 실패 테이블(preprocessing table)을 만들어 비교 횟수 최소화
- 동적 계획법 (Dynamic Programming)
- 하위 문제의 해를 저장하여 재계산 방지
- 해싱 (Hashing)
- O(1) 탐색을 위해 대량의 공간 사용
- 기수 정렬 (Radix Sort)
12-2 해싱
해싱이란?
- 공간을 이용해 시간을 극적으로 줄이는 탐색 기법

비유로 이해하는 해싱
아파트 단지에서 공용 우편함을 사용한다면 편지 찾기 어렵죠?
하지만 세대별 우편함이 있다면 금방 찾을 수 있어요.
→ 해싱은 바로 이런 개념!
데이터를 저장할 위치를 미리 계산해 바로 접근합니다.
해싱 vs. 다른 탐색법
| 탐색법 | 특징 | 조건 |
|---|---|---|
| 순차 탐색 | 처음부터 하나씩 비교 | 정렬 불필요 |
| 이진 탐색 | 중간값 기준으로 절반씩 탐색 | 정렬 필수 |
| 해싱 (Hashing) | 위치를 계산해 바로 접근 | 해시 함수 필요 |
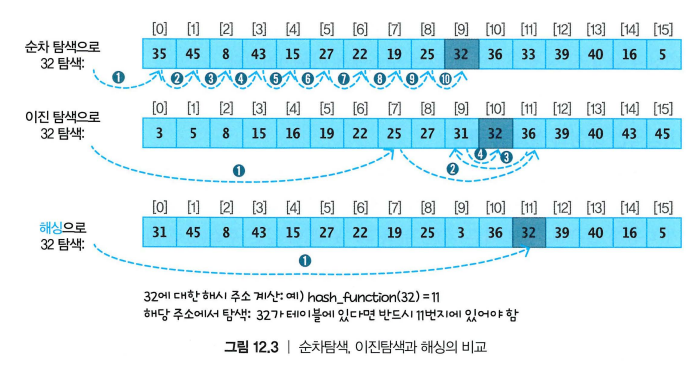
- 해싱은 이론상 한 번에 탐색 가능 (O(1))
- 단, 충돌(Collision)과 오버플로 문제 발생 가능
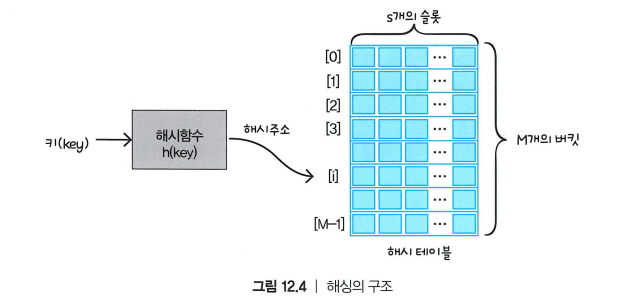
해싱의 구조
- 해시 테이블(Hash Table): 데이터를 저장하는 테이블
- 버킷(Bucket): 데이터가 들어가는 칸 (슬롯)
- 해시 함수(Hash Function): 키로부터 주소를 계산
# 숫자형 키에 대한 가장 기본적인 해시 함수
def hashFn(key):
return key % M # M은 테이블 크기충돌(Collision)과 오버플로란?
- 충돌: 서로 다른 키가 같은 주소를 가질 때
- 오버플로: 해당 주소에 빈 슬롯이 없을 때
- 예:
h("뉴욕") = 3
h("뮌헨") = 3 → 충돌 발생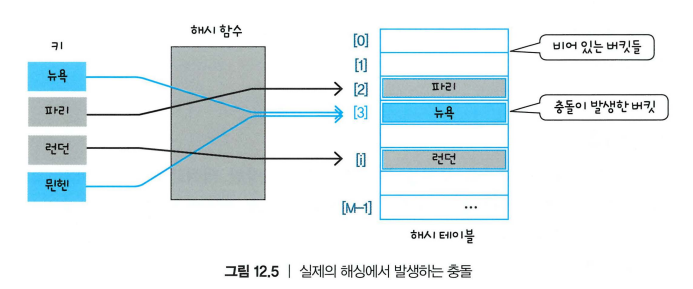
해시 함수
- 임의의 길이를 갖는 데이터를 고정된 길이의 데이터로 변환 시켜주는 함수
- 좋은 해시 함수의 조건
- 충돌이 적게 발생해야 합니다.
- 해시 결과가 테이블의 주소 영역 내에서 고르게 분포되어야 합니다.
- 계산이 빨라야 합니다.
1. 제산 함수(나머지 연산 함수)
-
나머지 연산자 mod(또는 % 연산자)
-
해시 테이블의 크기 M을 1과 자기 자신만을 약수로 가지는 소수(prime number)로 선택하는 것이 좋음
- 해시 주소를 좀 더 고르게 분포시키기 위해서
-
해싱에서 가장 흔히 사용되지만 항상 성능이 좋지는 않음
-
보완하기 위한 방법:
- 탐색 키를 몇 개의 부분을 나누어 더함
- 비트별 XOR 연산을 취하는 폴딩 기법
- 탐색 키를 제곱한 다음 중간에 몇 비트를 취함
- 숫자를 분석해 편중되지 않는 부분을 찾는 방법
2. 탐색키가 문자열인 경우
- 먼저 각 문자를 정수로 대응시켜야 함
- 예:
a부터z를1부터26에 대응시킬 수 있음- 문자의 아스키 코드나 유니코드값을 그대로 이용할 수 있음
- 문자열 안의 모든 문자를 골고루 사용하는 것이 좋음
def hashFnStr(key)
sum = 0
for c in key: # 문자열의 모든 문자에 대해
sum = sum + (ord(c)) # 그 문자의 아스키 코드값을 sum에 더함
return sum % M 오버플로 해결 방법
1. 개방 주소법 (Open Addressing)
- 빈 자리를 테이블 내 다른 곳에서 찾음
- 대표 방법: 선형 조사법 (Linear Probing)
# 충돌 발생 시 한 칸씩 이동하며 빈자리 찾음
while table[id] is not None:
id = (id + 1) % M- 문제점: 연속된 충돌 → 군집화(Clustering) 발생
- 해결책:
- 이차 조사법: 1, 4, 9, 16...처럼 제곱만큼 이동
- 이중 해싱: 다른 해시 함수를 하나 더 사용하여 이동 거리 결정
2. 체이닝 (Chaining)
- 하나의 버킷에 여러 항목 저장
- 리스트나 연결 리스트로 구현 가능
선형 조사법
- 첫 번째 전략 사용
- 계산된 주소에 빈 슬롯이 없으면 다음 주소(버킷)들을 순서에 따라 조사하여 빈 슬롯을 찾음
조사
- 비어 있는 공간을 찾는 것
- 예:
- 해시 테이블의 k번째 위치인
ht[k]에서 충돌이 발생했다면 다음 위치인ht[k+1]부터 순서대로 비어 있는지를 살피고, 빈 곳이 있으면 저장함
- 해시 테이블의 k번째 위치인
삽입 연산
- 해시 주소가 충돌하면 다음 주소를 순차적으로 확인
- 비어 있는 버킷이 나타날 때까지
+1씩 이동 - 예시
M = 13 # 해시 테이블 크기
table = [None] * M
def hashFn(key):
return key % M
def lp_insert(key):
id = hashFn(key)
count = M
while count > 0 and table[id] not in (None, -1): # 빈 버킷 또는 삭제된 자리(-1) 찾기
id = (id + 1) % M
count -= 1
if count > 0:
table[id] = key- 삽입 시나리오:
- 삽입 순서:
45 → 27 → 88 → 9 → 71 → 60 → 46 → 38 → 24

- 45, 27, 88, 9까지의 삽입은 문제 없음
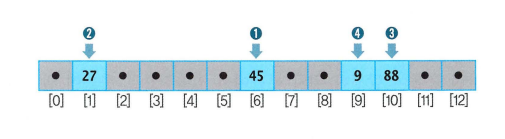
- 해시 주소 충돌 발생 시, 선형 탐색으로 빈 슬롯을 찾음
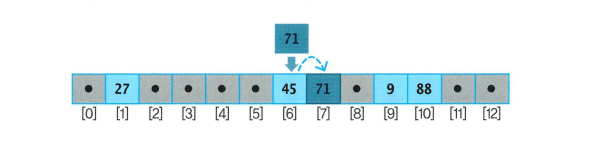
- 마지막
24는 끝까지 가도 비어 있는 자리가 없어서 테이블 맨 앞으로 되돌아와 저장됨
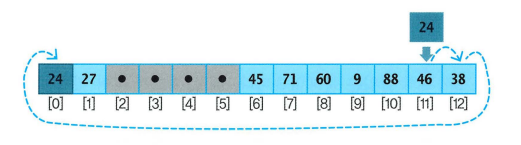
- 삽입 순서:
- 주의:
- 군집화(clustering) 현상이 발생 가능
(충돌 근처에 데이터가 몰림 → 탐색 시간 증가)
- 군집화(clustering) 현상이 발생 가능
탐색 연산
- 해시 주소를 기준으로, 키가 일치할 때까지
+1씩 이동 - 빈 슬롯(None)을 만나면 해당 키는 테이블에 존재하지 않음
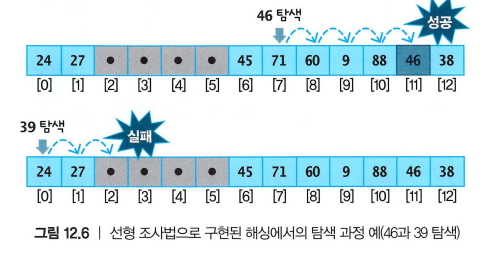
- 예:
def lp_search(key):
id = hashFn(key)
count = M
while count > 0:
if table[id] == None:
return None # 테이블에 없음
if table[id] == key:
return table[id] # 키 발견
id = (id + 1) % M
count -= 1
return Nonelp_search(46)→ 충돌을 피해 선형 조사 후 위치 찾기 성공lp_search(39)→ 중간에 빈 슬롯(None)을 만나 탐색 실패
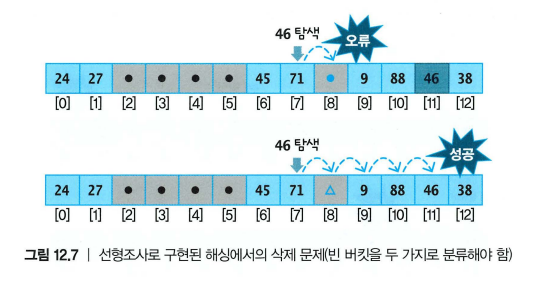
삭제 연산
- 문제점:
- 단순히
None으로 지우면 이후 탐색이 끊겨 탐색 실패 가능성 발생 - 예:
60을 먼저 삭제하면,46탐색 시 중간에 멈춰버림
- 단순히
- 해결 방법
- 삭제된 슬롯을 특수값 -1로 표시
- 탐색 중
-1은 "지워졌지만 지나가야 하는 자리"로 인식됨
- 코드 예시
def lp_delete(key):
id = hashFn(key)
count = M
while count > 0:
if table[id] == None:
return # 없음
if table[id] != -1 and table[id] == key:
table[id] = -1 # 삭제 마킹
return
id = (id + 1) % M
count -= 1- 삽입 시
-1을 빈 슬롯처럼 인식하도록 변경 필요:
while count > 0 and table[id] not in (None, -1):- 보완 전략
| 방법 | 특징 |
| ----------------------------- | ----------------------------------- |
| 🔁 이차 조사법 (Quadratic Probing) |+1, +4, +9, ...식으로 증가. 군집화 완화 가능 |
| 🔁 이중 해싱 (Double Hashing) | 두 번째 해시 함수로 이동 거리 계산. 분산 효과 우수 |
12-3 백트래킹
백트래킹이란?
- 해를 찾기 위한 모든 경우의 수를 시도하되, 중간에 해가 될 수 없다고 판단되면 그 분기점을 건너뛰는 방식
- 상태 공간 트리(state space tree)에서 유망하지 않은 노드를 미리 제거하는 가지치기(pruning)로 효율을 높임
- 예시: 미로 찾기
- 길이 갈라지는 지점에서 한 방향을 선택해 가다가, 길이 막히면 다시 되돌아와 다른 길을 시도하는 방식 → 백트래킹
상태 공간 트리란?
- 틱택토(TicTacToe)나 N-Queen처럼 가능한 모든 상태(배치/수)를 트리 구조로 표현한 것이 상태 공간 트리임
- 예:
- 3x3 틱택토 게임의 모든 가능성을 트리로 그리면, 총 9! = 362,880개의 노드가 생김
- 백트래킹을 사용하면 그 중 대부분을 탐색하지 않아도 됨
N-Queen 문제 소개
문제 정의
- NxN 체스판 위에 N개의 퀸(Queen)을 놓되, 서로 공격하지 못하도록 배치하는 문제
- 퀸은 가로, 세로, 대각선 방향으로 공격이 가능
- 따라서 어느 두 퀸도 같은 행/열/대각선에 있어선 안 됨
브루트포스 vs 백트래킹
| 전략 | 설명 | 연산량 |
|---|---|---|
| 브루트포스 | N² 칸 중 N개를 무작위 선택 후 유효성 검사 | C(N², N) (조합) |
| 백트래킹 | 한 행씩 퀸을 두며 유망하지 않으면 되돌아감 | 훨씬 적은 탐색 |
- 백트래킹은 수십 가지 탐색만으로 정답에 도달 가능함 (예: 4-Queen의 해는 단 2가지)
N-Queen 백트래킹 알고리즘
유효성 검사 함수
- 해당 위치 (x, y)에 퀸을 놓을 수 있는지 검사함
def isSafe(board, x, y):
N = len(board)
# 세로 방향
for i in range(y):
if board[i][x] == 1:
return False
# 왼쪽 대각선 ↖
for i, j in zip(range(y-1, -1, -1), range(x-1, -1, -1)):
if board[i][j] == 1:
return False
# 오른쪽 대각선 ↗
for i, j in zip(range(y-1, -1, -1), range(x+1, N)):
if board[i][j] == 1:
return False
return True재귀적 백트래킹 함수
def solve_N_Queen(board, y):
N = len(board)
if y == N: # 모든 행에 퀸을 놓았다면 출력
printBoard(board)
print()
return
for x in range(N):
if isSafe(board, x, y):
board[y][x] = 1
solve_N_Queen(board, y + 1)
board[y][x] = 0 # 백트래킹출력 함수 및 실행 코드
def solve_N_Queen(board, y):
N = len(board)
if y == N: # 모든 행에 퀸을 놓았다면 출력
printBoard(board)
print()
return
for x in range(N):
if isSafe(board, x, y):
board[y][x] = 1
solve_N_Queen(board, y + 1)
board[y][x] = 0 # 백트래킹- 실행 결과
. Q . .
. . . Q
Q . . .
. . Q .
. . Q .
Q . . .
. . . Q
. Q . .