백준 1309(동물원)

안녕하세요!

오늘은 알고리즘 문제를 풀어볼까해요.

한동안 알고리즘 문제를 안풀어서... 반성하고 간단해 보이는 문제로 스타트해보겠습니다.

오늘 풀 문제는 동물원이라는 DP문제에요. 난이도는 실버1입니다.

문제

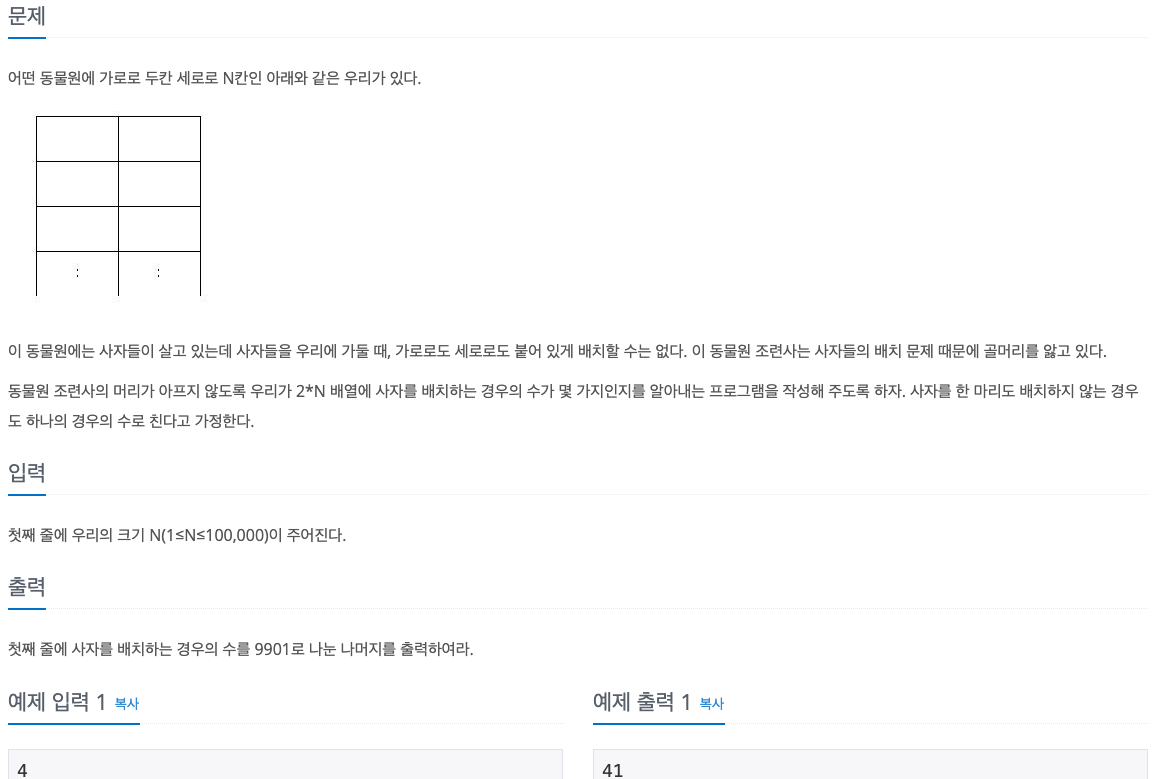
문제를 간략히 설명 드리면 고정으로 2개의 열과 N개의 행으로 구성된 이차원 배열을 사용하여 사자를 위치시킬 수 있는 경우의 수를 찾는 문제입니다. 단, 사자를 가로로도 세로로도 붙어있게 배치할 수 없습니다.

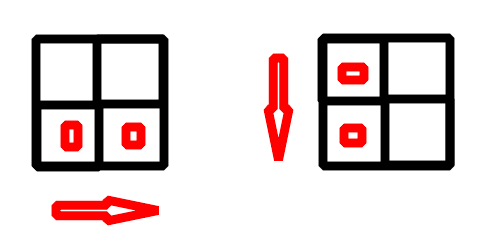
저는 처음에 가로로도 세로로도 붙어있게 배치 못한다는게 무슨 말인지를 이해하기 힘들어서 몇번 지문을 읽었네요... 대충 말씀드리면 아래 사진과 같이 배치 못 한다는 말입니다! 그렇다면, 지그재그로 사자를 배치해야겠죠?

풀이

우선 지그재그로 사자를 배치하고 경우의 수를 파악하기 위해 2차원 배열 dp[N][3]을 구성하겠습니다.

dp[N][1]이 왼쪽 셀에 사자가 들어가는 경우의 수, dp[N][2]가 오른 셀에 사자가 들어가는 경우의 수를 담고 사자를 배치하지 않는 경우는 dp[N][0]에 기록하겠습니다.

그 다음으로 아래와 같이 N에 숫자를 대입해보고 점화식을 새워보겠습니다.

N == 1) 왼쪽에 한번, 오른쪽에 한번 그리고 배치하지 않는 경우 한번이 되겠죠?

N == 2) 
오른쪽에 사자를 배치하기 위해서는 이전에 왼쪽에 사자를 배치했거나 사자를 배치하지 않는 경우겠죠?

왼쪽에 사자를 배치하기 위해서는 이전에 오른쪽에 사자를 배치했거나 사자를 배치하지 않는 경우겠죠?

사자를 배치하지 않는 경우는 이전에 어떤 위치에 사자가 있던 관계가 없겠죠?

위를 잘 생각해보면 아래와 같은 점화식이 나올거에요.

dp[i][0] = dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2];
dp[i][1] = dp[i - 1][0] + dp[i - 1][2];
dp[i][2] = dp[i - 1][1] + dp[i - 1][0];

점화식이 나왔으면 코드는 금방 작성하실거라 믿습니다!

코드

Code 보기

public class Main {
  public static final int n = 100000;

  public static void main(String[] args) throws IOException {
      BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
      int row = Integer.parseInt(br.readLine());
      int dp[][] = new int[row][3];

      if(row > n){
          throw new ArrayIndexOutOfBoundsException("범위 초과");
      }

      //init
      dp[0][0] = 1;
      dp[0][1] = 1;
      dp[0][2] = 1;
      for(int i = 1; i < row; i++){
          dp[i][0] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2]) % 9901;
          dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % 9901;
          dp[i][2] = (dp[i - 1][1] + dp[i - 1][0]) % 9901;
      }

      int result = (dp[row-1][0] + dp[row-1][1] + dp[row-1][2]) % 9901;
      System.out.println(result);
  }
}
  

• 접기/펼치기는 왜 미리보기에서만 될까요...?