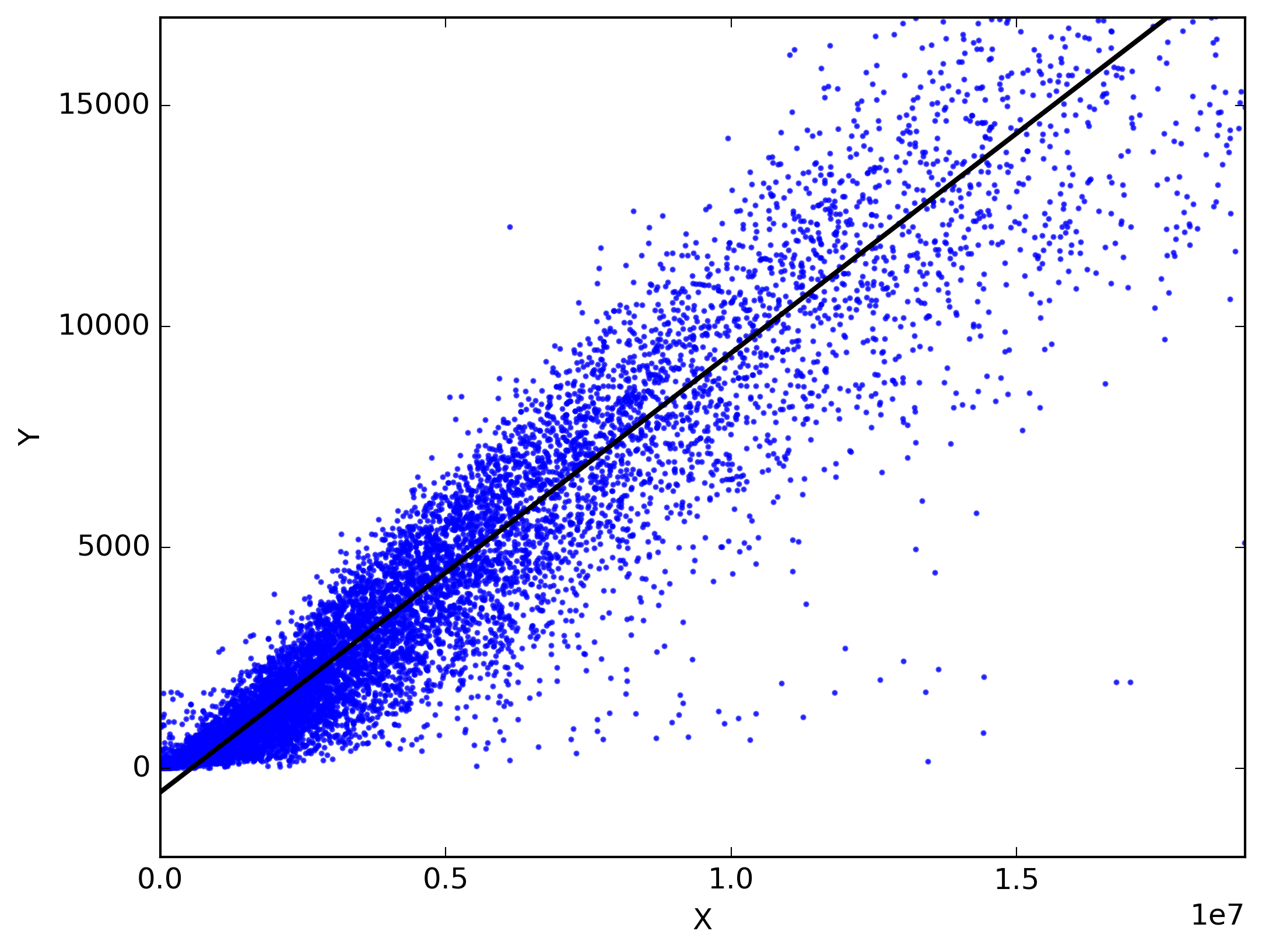
딥러닝은 복잡한 연산으로 이루어져 있지만 이해를 위해 딥러닝 말단에서 진행되는 계산인 선형 회귀와 로지스틱 회귀부터 살펴볼 예정입니다.
1. 선형 회귀 개요
1.1. 선형 회귀의 정의
- 선형 회귀(linear regression)란 독립변수를 사용해 종속변수의 움직임을 예측하고 설명하는 작업을 의미합니다.
- 단순 선형 회귀(simple linear regression)
- 하나의 독립변수를 이용하여 종속변수의 동작을 예측하는 것
- 다중 선형 회귀(multiple linear regression)
- 여러 독립변수를 이용하여 종속변수의 동작을 예측하는 것
1.2. 예측선
- 데이터에서 주어진 점들의 특징을 담은 선이 직선의 형태인 경우 일차함수로 나타낼 수 있습니다. 이러한 직선은 선형회귀를 통해 얻은 예측선입니다.
- 선형 회귀를 통해 예측해야 하는 것은 주어진 데이터의 특성을 잘 반영한 최적의 직선의 기울기와 절편입니다.
2. 오차
2.1 최소제곱법
-
최소제곱법(least squar method)은 일차함수의 기울기와 절편을 구할 수 있는 방법입니다. 주어진 데이터가 입력값 와 출력값 인 경우에는 다음과 같이 기울기 와 절편 를 다음과 같이 구할 수 있다.
, 는 평균을 의미
Python을 이용한 최소제곱법 계산
- 최소제곱법을 계산하기 위해서는 numpy 라이브러리를 이용해야 한다.
import numpy as np- 데이터를 다룰 배열 생성
x = np.array([ ... ])
y = np.array([ ... ])- 평균 계산
mx = np.mean(x)
my = np.mean(y)- 최소제곱법 계산
# 기울기 공식의 분모 계산
divisor = sum([(i-mx)**2 for i in x])
# 기울기 공식의 분자 계산
def top(x, mx, y, my):
d = 0
for i in range(len(x)):
d += (x[i] - mx) * (y[i] - my)
return d
dividend = top(x, mx, y, my)
# 기울기 계산
a = dividend/divisor
# y 절편 계산
b = my - (mx*a)
2.2 평균 제곱 오차
-
최소제곱법은 여러 입력을 처리하기에는 무리가 있기 때문에 실제로 사용하기 어렵습니다. 그래서 입력별로 조금씩 수정해나가는 평균 제곱 오차(mean squre error, MSE) 방법을 사용할 수 있습니다.
-
평균 제곱 오차 (MSE)
는 실제값는 예측선을 통해 얻은 값 -
선형 회귀는 임의의 직선을 그어 이에 대한 평균 제곱 오차를 구하고, 이 값을 가장 작게 만들어 주는 기울기와 절편 값을 찾아가는 작업입니다.
Python을 이용한 평균 제곱 오차 계산
- 임의의 기울기와 절편 지정
# 임의의 기울기와 y 절편 지정
fake_a = 3
fake_b = 76
# 임의의 직선에 대한 예측
def predict(x):
return fake_a * x + fake_b
# 결과값이 들어갈 빈 리스트 생성
predict_result = []
# 예측값 채우기
for i in range(len(x)):
predict_result.append(predict(x[i]))
print( ... )- 평균 제곱 오차 계산
# 평균 제곱 오차를 이용하여 최종 값 구하기
n = len(x)
def mse(y, y_pred):
return (1/n) * sum((y - y_pred)**2)
3. 경사하강법
3.1. 경사하강법
MSE와 같은 알고리즘을 통해 오차를 계산할 수 있습니다. 이렇게 구한 오차를 이용하여 최소 오차를 갖는 기울기를 찾아야 합니다. 예측선의 기울기와 오차 사이의 관계는 이차함수 관계입니다. 그렇기 때문에 이차함수의 성질을 생각해보면 미분계수가 0인 지점에서 오차가 최소라고 판단할 수 있습니다. 미분을 이용하여 기울기가 0인 지점(오차가 가장 작은 지점)을 찾는 방법을 경사하강법(gradient decent)이라 합니다.
3.2. 경사하강법 알고리즘
-
에서의 미분값을 구한다. (초기인 경우 임의의 지점)
-
구한 기울기(미분값)의 반대방향으로 일정 거리만큼 이동시킨 지점 에서 미분을 구한다.
-
미분값이 0이 아닌 경우 를 으로 하여 1.과 2. 과정을 반복한다.
3.3. 학습률 (learning rate)
경사하강법 알고리즘을 보면 미분값이 0이 아닌 경우 반대방향으로 일정 거리만큼 이동시키게 됩니다. 이때 이동시키는 거리를 가중치와 가중치에 곱해지는 비율을 통해 결정하는데 곱해지는 비율을 학습률이라 합니다.
아래 그림은 학습률에 따른 경사하강법의 수렴과 발산을 나타내는 그림입니다. 학습률이 너무 작으면 효율이 떨어지게 되고, 학습률이 지나치게 크면 수렴하지 못하고 발산하는 양상을 보이게 됩니다.
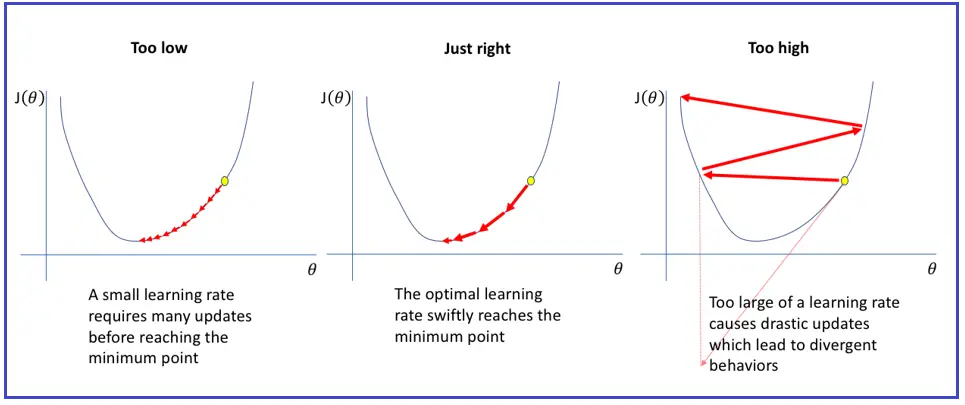
결론적으로 경사하강법은 오차와 기울기에 대한 이차함수 그래프를 만들고 적절한 학습률을 설정하여 미분이 0이 되는 지점을 구하는 과정이라 할 수 있습니다.
4. Python을 이용한 선형회귀
4.1. 선형회귀 알고리즘 구현
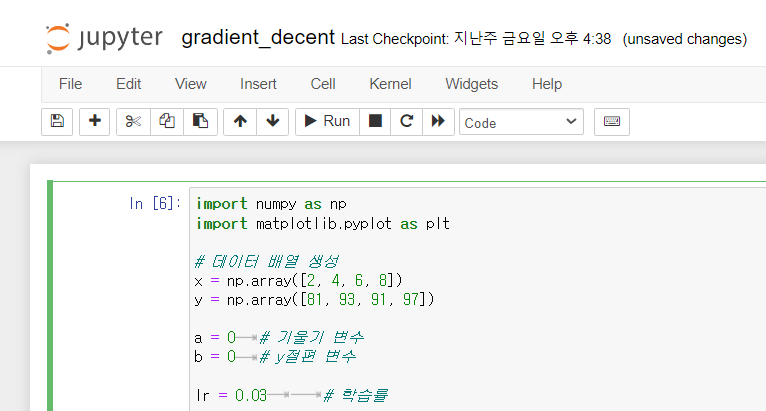
import numpy as np
import matplotlib.pyplot as plt
# 데이터 배열 생성
x = np.array([2, 4, 6, 8])
y = np.array([81, 93, 91, 97])
a = 0 # 기울기 변수
b = 0 # y절편 변수
lr = 0.03 # 학습률
epochs = 2001 # 반복횟수
n = len(x)
# 경사하강법
for i in range(epochs):
y_pred = a * x + b # 예측값 계산
error = y - y_pred # 오차 계산
a_diff = (2/n) * sum(-x * (error)) # 기울기에 대한 편미분
b_diff = (2/n) * sum(-(error)) # y절편에 대한 편미분
a = a - lr * a_diff
b = b - lr * b_diff
# 경사하강법을 통해 얻은 직선 출력
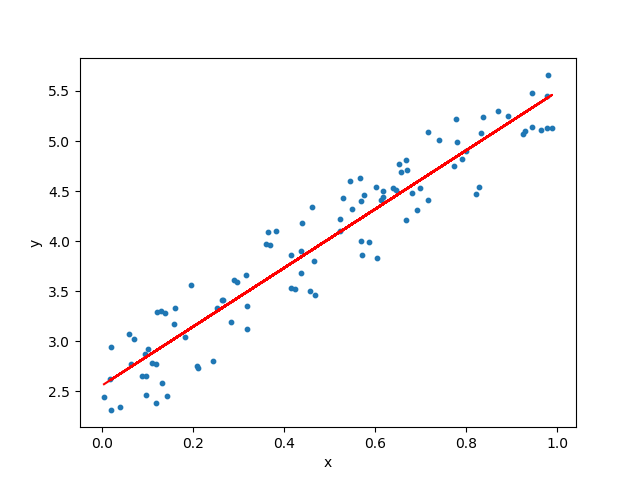
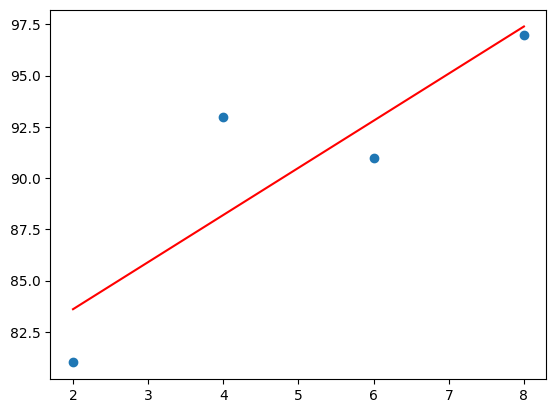
y_pred = a * x + b
plt.scatter(x, y)
plt.plot(x, y_pred,'r')
plt.show()
4.2. 실행하기
- 그래프 출력을 위해
matplotlib가 없는 경우 다음과 같이 터미널에 입력하여 설치한다.
pip install matplotlib
- 다음과 같이 터미널에 입력하여 프로젝트를 수행할 환경 활성화하고 jupyter notebook에 접속한다.
> conda activate deep_learning
> jupyter notebook
- 실습 코드를 실행한다.
- jupyter notebook
- 결과 그래프
5. 다중선형회귀(Multiple Linear Regression)
5.1. 다중선형회귀
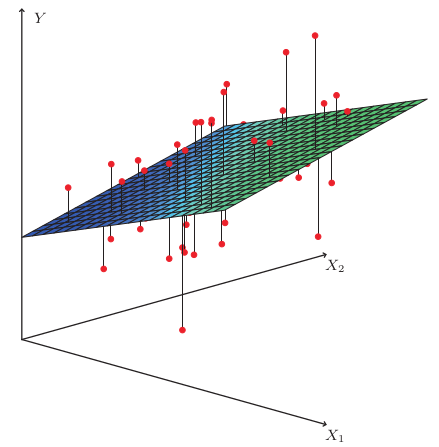
단순선형회귀에서는 하나의 독립변수에 대한 종속변수의 변화에 대한 예측선을 그리는 작업을 진행하였습니다. 하지만 실제로 예측해야 하는 일들은 여러 독립변수가 작용하기 때문에 정확한 예측을 위해서는 다른 특성을 추가해야 합니다. 이렇게 여러 독립변수를 이용하여 종속변수를 예측하는 것을 다중선형회귀라 합니다.
5.2. 단순선형회귀 vs 다중선형회귀
단순선형회귀는 직선을 찾는 과정이었습니다. 다중선형회귀가 찾을 것은 여러 독립변수에 대한 선형결합으로, 공간 상에서의 평면을 찾는 과정이라 할 수 있습니다.
5.3. Python을 이용한 다중선형회귀
import numpy as np
import matplotlib.pyplot as plt
# 1. 데이터 배열 생성
x1 = np.array([...])
x2 = np.array([...])
y = np.array([...])
# 2. 기울기와 y 절편의 값을 초기화
a1 = 0
a2 = 0
b = 0
# 3. 학습률 설정
lr = 0.01
# 4. 반복 횟수 설정
ephchs = 2001
# 5. 경사하강법 수헹
n = len(x1)
for i in range(epochs):
# 5.1. 예측식과 오차 계산
y_pred = a1 * x1 + a2 * x2 + b
error = y - y_pred
# 5.2. 오차 함수를 편미분
a1_diff = (2/n) * sum(-x1 * (error))
a2_diff = (2/n) * sum(-x2 * (error))
b_diff = (2/n) * sum(-(error))
# 5.3. 학습률을 곱해 예측식에 사용되는 변수 업데이트
a1 = a1 - lr * a1_diff
a2 = a2 - lr * a2_diff
b = b - lr * b_diff
# 6. 결과 출력
print("실제 점수: ", y)
print("예측 점수: ", y_pred
6. Tensorflow에서 실행하는 선형회귀모델
6.1. 머신 러닝에서의 선형회귀
머신러닝은 선형회귀와 같은 분석 방법을 이용하여 예측 모델을 만드는 것입니다. 선형회기를 하면서 다뤘던 개념들은 머신러닝에서는 다음과 같이 사용합니다.
이전에는 선형회귀를 이용하여 예측하기 위한 식을 세웠습니다. 머신러닝에서는 이를 가설 함수라 하고 로 표기합니다. 식에서 기울기와 y 절편은 각각 가중치(weight; )와 편향(bias; )라고 합니다.
평균제곱오차처럼 실제 값과 예측 값 사이의 오차에 대한 식은 손실 함수(loss function)라 합니다.
경사하강법은 딥러닝에서 옵티마이저(optimizer)라고 합니다.
용어 정리
-
예측식 가설함수
-
평균 제곱 오차 손실 함수
-
경사 하강법 옵티마이저
6.2. Tensorflow를 이용한 선형회귀
우선 실행하기 앞서 다음과 같은 함수들이 필요합니다.
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
선형회귀를 실행하는 코드는 다음과 같습니다.
model.add(Dense(1, input_dim=1, activation='linear'))
model.compile(optimizer='sgd', loss='mse')
model.fit(x, y, epochs=2000)
Dense()
-
첫번째 인자는 출력되는 값의 수를 의미합니다. 예제에서는 출력되는 값이 하나씩 이므로 1로 두었습니다.
-
두번째 인자(input_dim)는 입력되는 값의 수를 의미합니다. 예제에서는 하나씩 입력하므로 1로 두었습니다.
-
세번째 인자(activation)은 입력된 값을 다음 층으로 어떻게 처리하여 넘길지를 결정하는 함수인 활성화 함수를 설정하는 옵션입니다. 기본값은
'linear'입니다. 선형 회귀를 다루고 있으므로 따로 추가하지 않거나activation='linear'을 추가하면 됩니다.
model.compile()
-
경사하강법을 실행하기 위해서 옵티마이저 부분에
optimizer='sgd'를 입력합니다. -
손실 함수는 평균제곱오차를 사용할 것이므로
loss='mse'를 입력합니다.
model.fit()
- 입력배열, 출력배열, 반복 횟수 순서대로 추가합니다.
이렇게 생성한 모델의 예측값은 model.predict()에 입력값을 인수로 주어 확인할 수 있습니다.
6.3. Python으로 실행해보기
다음과 같이 프로젝트 폴더를 생성하여 jupyter notebook을 실행합니다.

6.3.1. 단순선형회귀
- 예제 코드
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# 주어진 데이터
x = np.array([2, 4, 6, 8])
y = np.array([81, 93, 91, 97])
# 단순선형회귀 모델 생성
model = Sequential()
model.add(Dense(1, input_dim=1, activation='linear'))
model.compile(optimizer='sgd', loss='mse')
model.fit(x, y, epochs=2000)
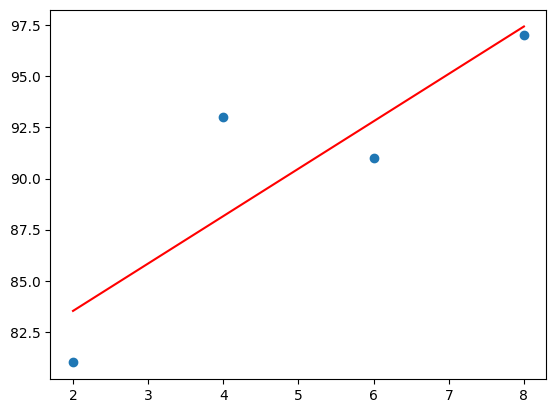
# 결과 그래프 출력
plt.scatter(x, y)
plt.plot(x, model.predict(x), 'r')
plt.show()
# 임의의 입력을 이용하여 결과를 예측해보기
t = 3
prediction = model.predict([t])
print("입력: %.f, 예상 결과: %.02f" % (t, prediction))- 실행 결과
- 결과 그래프
- 예측값
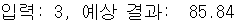
- 결과 그래프
6.3.2. 다중선형회귀
다중선형회귀의 경우 독립변수의 수가 많아지므로 Dense() 함수에서 input_dim에 해당하는 인수에 입력으로 넣어주는 독립변수의 수만큼 설정해줘야 합니다.
예측 결과를 구하기 위해서는 똑같이 model.predict() 함수를 사용하지만 독립변수에 맞춰 리스트로 인수를 넘겨줘야 합니다.
- 예제 코드
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# 주어진 데이터
x = np.array([[2, 0], [4, 4], [6, 2], [8, 3]])
y = np.array([81, 93, 91, 97])
# 다중선형회귀 모델 생성
model = Sequential()
model.add(Dense(1, input_dim=2, activation='linear'))
model.compile(optimizer='sgd', loss='mse')
model.fit(x, y, epochs=2000)
# 임의의 입력을 이용하여 결과를 예측해보기
t1 = 7
t2 = 4
prediction = model.predict([[t1, t2]])
print("입력 1: %.f, 입력 2: %.f, 예상 결과: %.02f" % (t1, t2, prediction))- 실행 결과
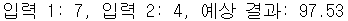
Reference
- 해당 글은 "모두의 딥러닝" 5장을 기반으로 작성되었습니다.
- 조태호. 모두의 딥러닝 (개정3판). 길벗(2022)
Reference
- 해당 글은 "모두의 딥러닝" 4-5장을 기반으로 작성되었습니다.
- 조태호. 모두의 딥러닝 (개정3판). 길벗(2022)