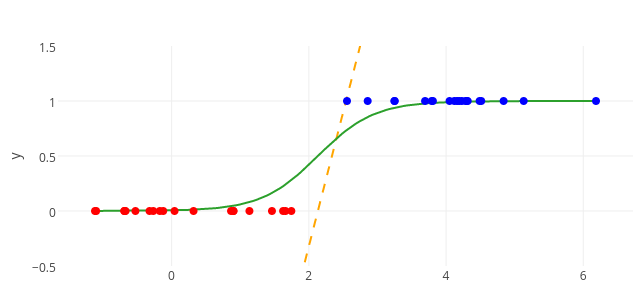
로지스틱 회귀는 '예' 혹은 '아니요'와 같이 참과 거짓 중 하나를 내놓는 과정을 위해 사용됩니다.
1. 로지스틱 회귀
1.1. 선형회귀의 한계
종속변수가 기존의 모델처럼 여러 값이 아니라 이진 관계의 결과값을 가지는 경우에는 선형 회귀는 적절한 예측으로 보기 어렵습니다. 이러한 경우에는 직선이 아니라 이진 관계의 결과 사이를 구분하는 S자 형태의 곡선을 이용해야 합니다.
1.2. 시그모이드 함수
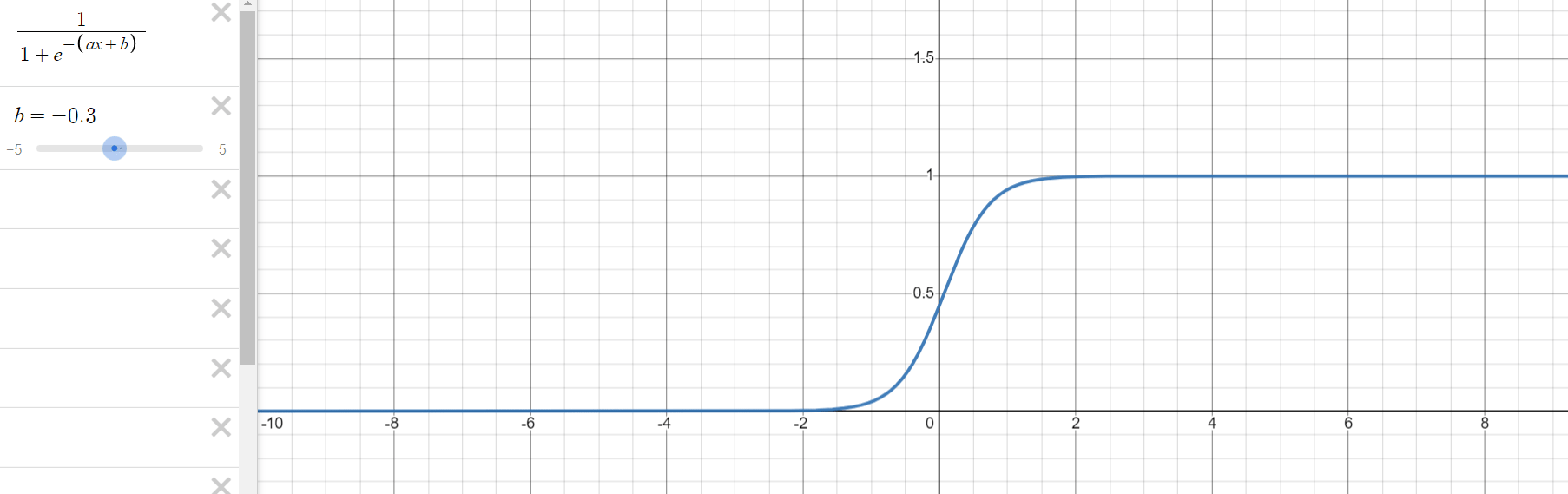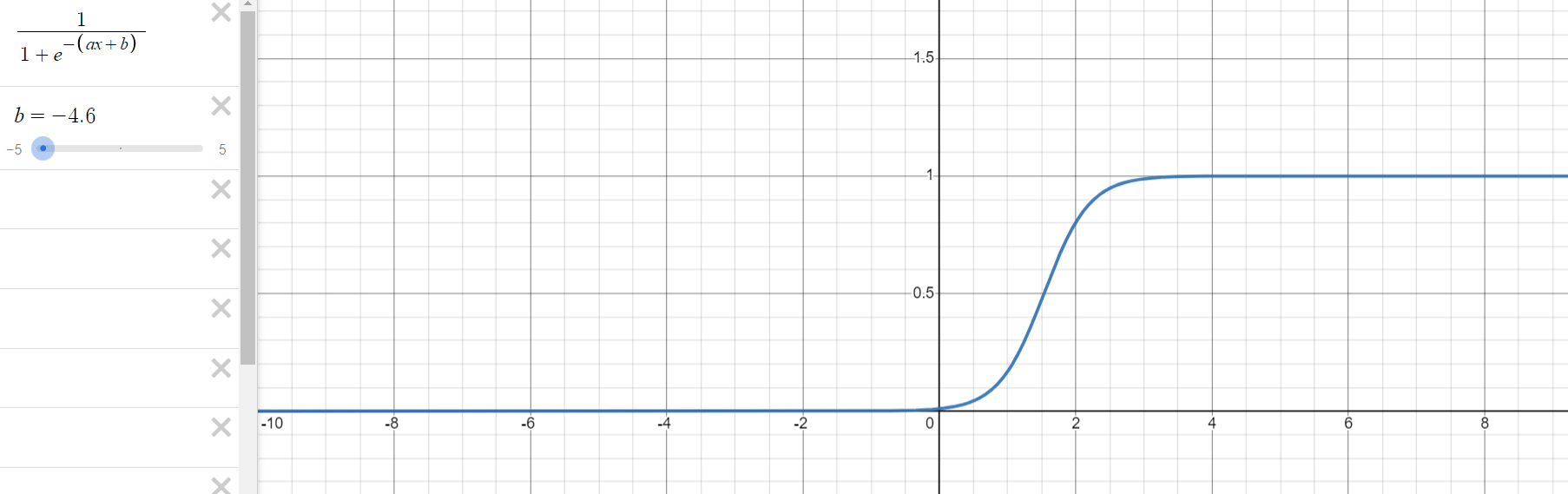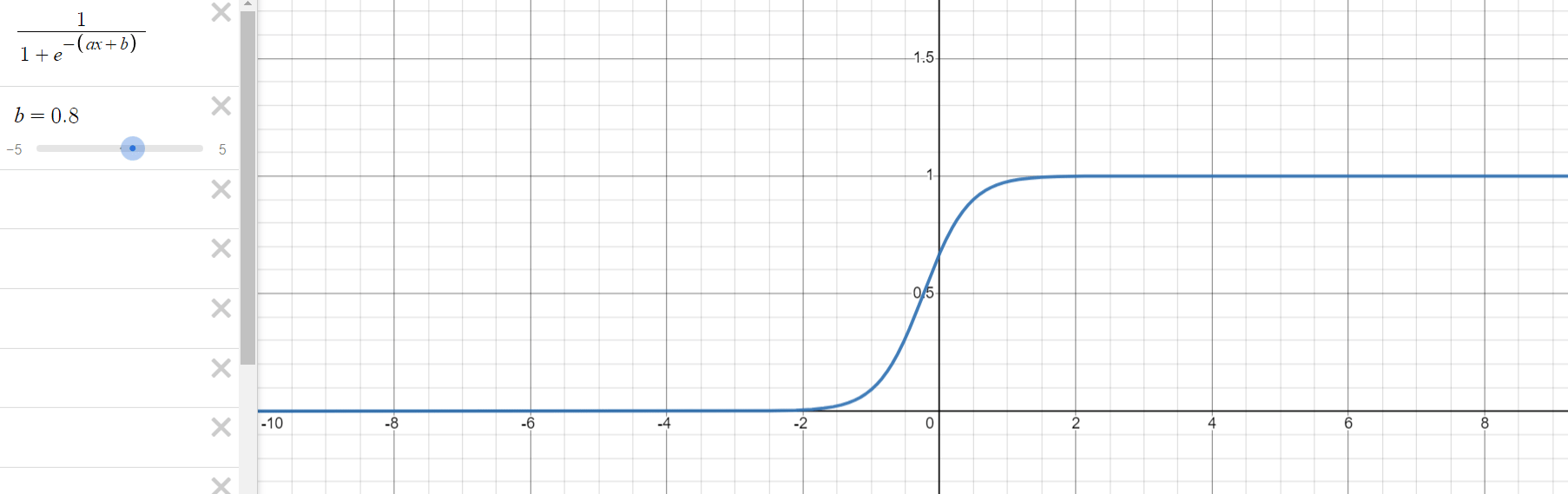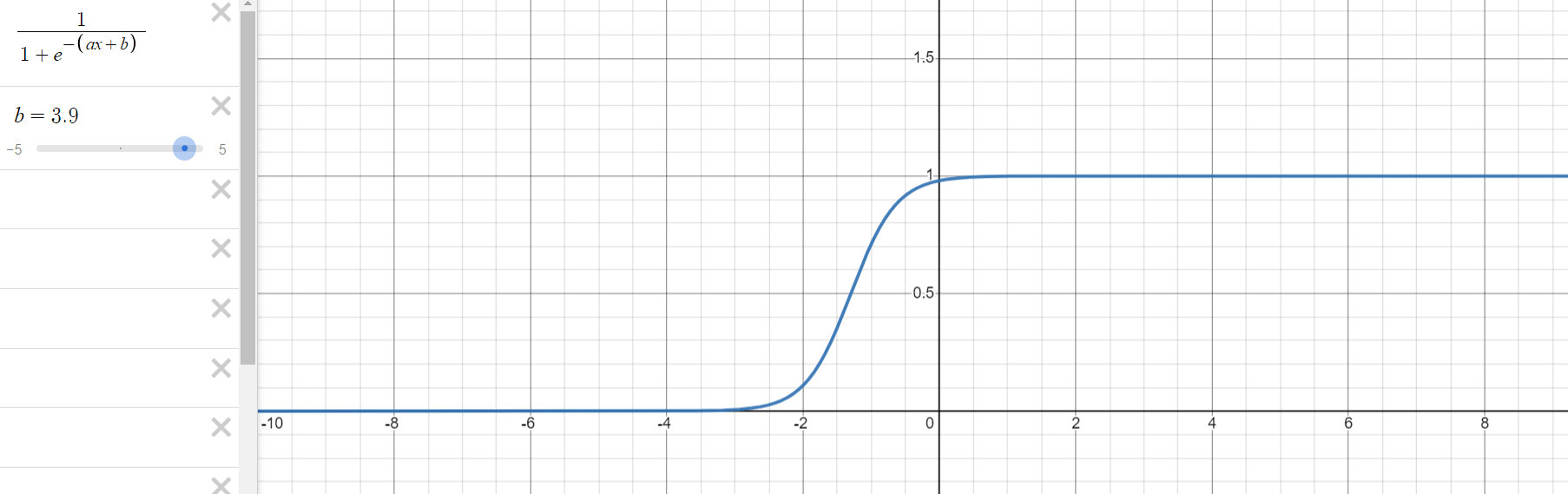
앞서 3장에서 다뤘던 시그모이드 함수가 S자 형태로 그래프가 그려지기 때문에 로지스틱 회기분석에서는 시그모이드 함수를 이용합니다. 시그모이드 함수의 수식은 다음과 같습니다.
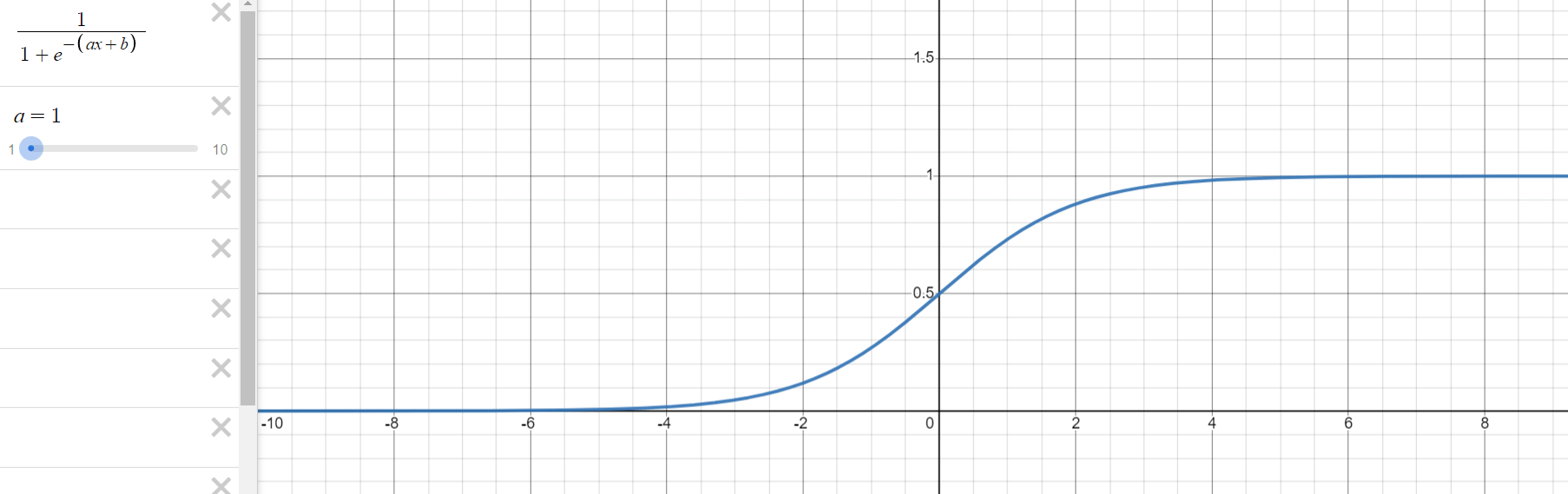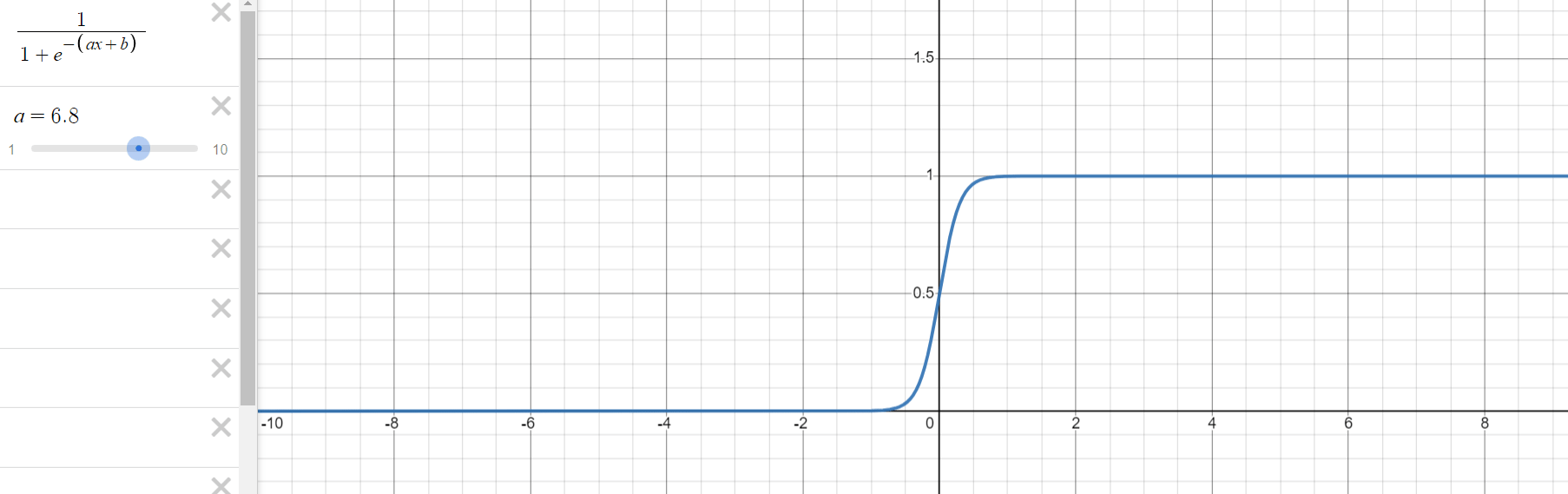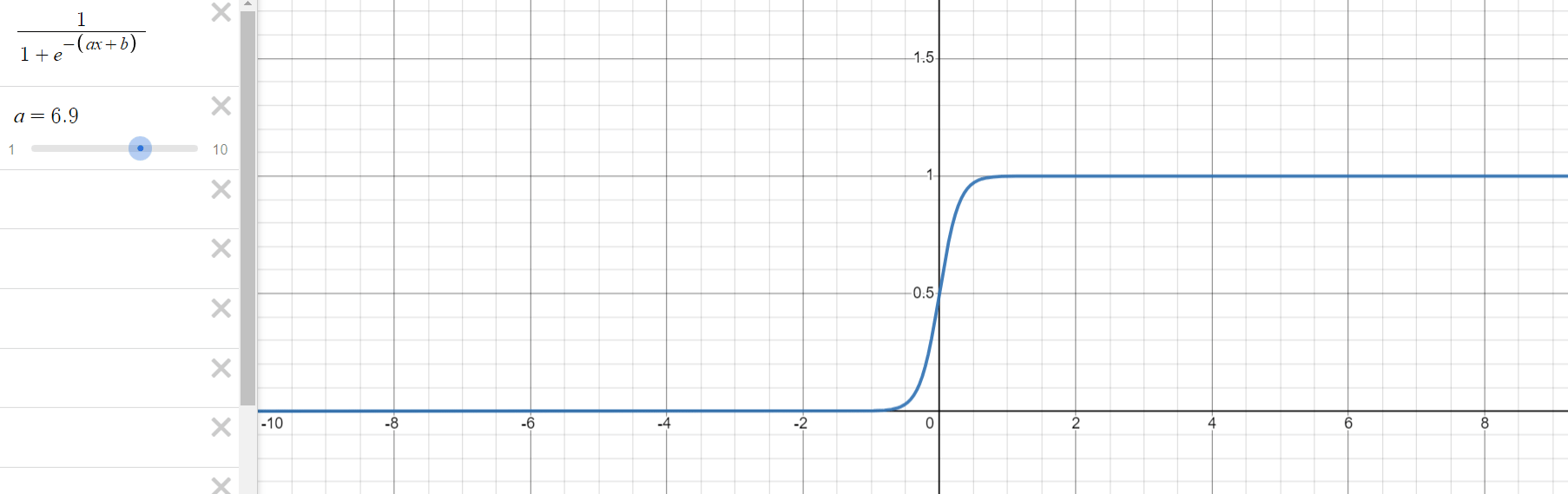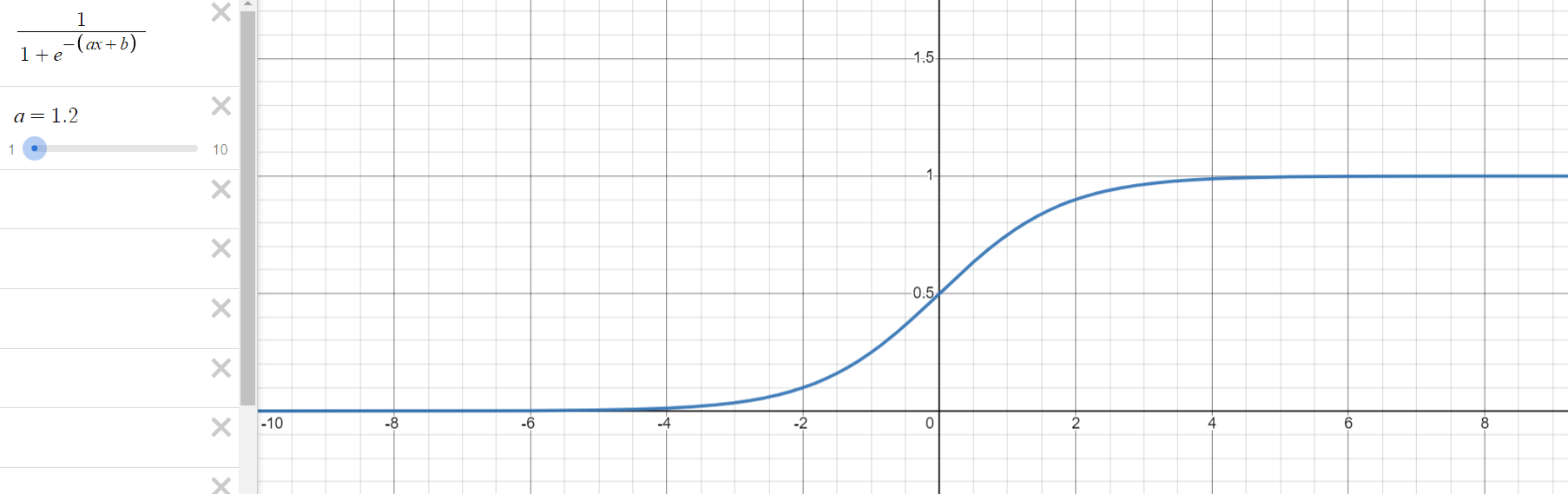
로지스틱 회귀 과정을 통해 구해야 하는 것은 위의 식에서 와 입니다. 는 그래프의 경사도를 결정하는 값으로 값이 클수록 경사가 커집니다. 는 중심의 위치를 결정하는 값으로 절대값의 크기에 따라 부호의 반대 방향으로 이동합니다.
- 의 변화에 따른 그래프의 변화
- 의 변화에 따른 그래프의 변화
1.3. 오차
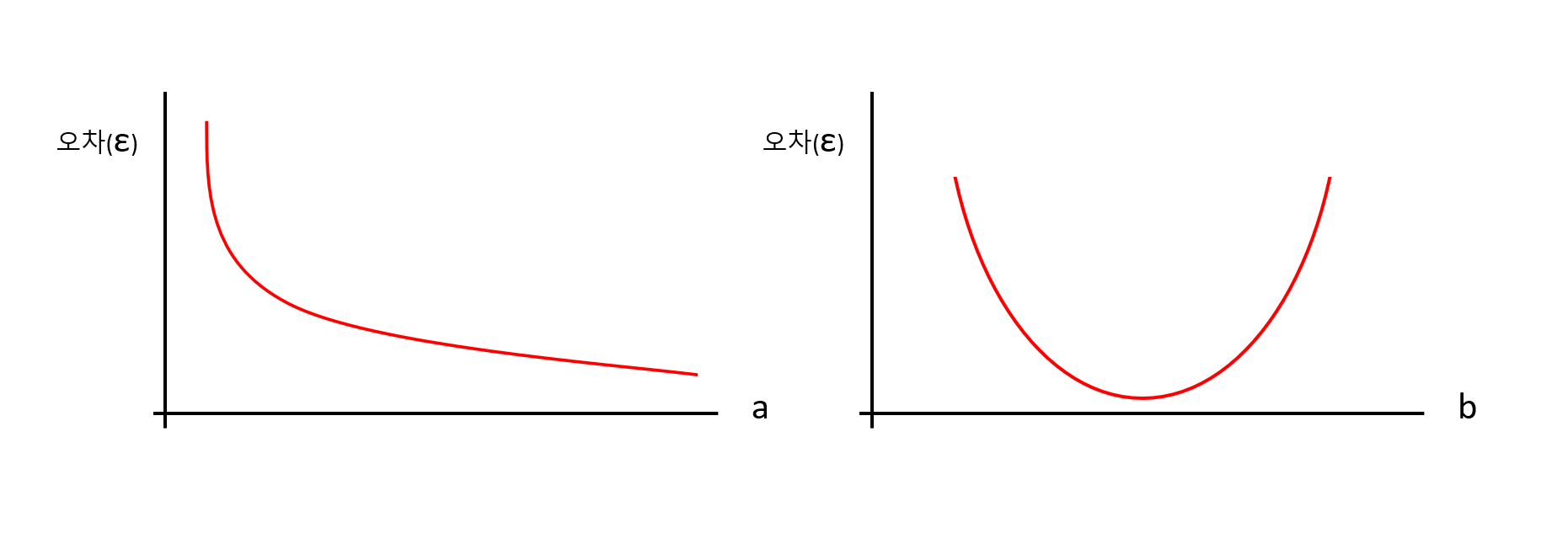
로지스틱 회귀에서도 선형 회귀와 마찬가지로 오차가 가장 작은 , 를 찾아야 합니다. , 와 오차 사이의 관계는 다음과 같은 그래프로 그려집니다.
2. 오차 공식
로지스틱 회귀에서도 와 를 찾을 때는 경사 하강법을 사용해야 합니다. 경사 하강법을 사용하기 위해서는 오차를 구해야 하는데 시그모이드 함수는 종속변수의 값이 0과 1 사이에 있으므로 선형 회귀에서 사용했던 평균제곱오차를 사용하기는 어렵습니다. 로지스틱 회귀에서는 로그함수를 이용하여 오차를 구할 수 있습니다.
2.1. 교차 엔트로피 오차 함수
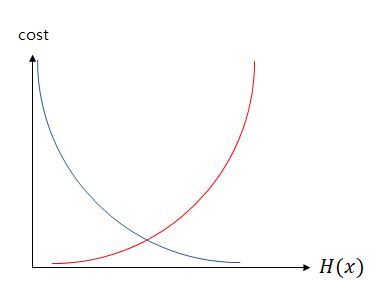
위의 그래프에서 파란색 선은 실제 값이 1일 때 오차가 0이 되는 로그함수 그래프이고, 빨간색 선은 실제 값이 0일 때 오차가 되는 로그함수 그래프 입니다. 각각 수식으로 파란색 그래프는 이고 빨간색 그래프는 입니다. 종속변수 의 값이 1일 때는 파란색 수식을 사용하고 0일 때는 빨간색 수식을 사용합니다. 이를 종합하면 다음과 같은 수식을 얻을 수 있습니다.
위의 함수가 로지스틱 회귀에서 사용할 수 있는 손실 함수입니다. 이 함수를 머신러닝에서는 교차 엔트로피 오차(cross entropy error) 함수라고 합니다.
3. Tensorflow에서 실행하는 로지스틱회귀 모델
Dense()함수에서 활성화 함수를 시그모이드 함수로 지정합니다.activation='sigmoid'
model.compile()부분에서 손실 함수를 교차 엔트로피 오차 함수로 지정합니다.loss='binary_crossentropy'
- 예제 코드
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# 주어진 데이터
x = np.array([2, 4, 6, 8, 10, 12, 14])
y = np.array([0, 0, 0, 1, 1, 1, 1])
# 로지스틱 회귀 모델 생성
model = Sequential()
model.add(Dense(1, input_dim=1, activation='sigmoid'))
model.compile(optimizer='sgd', loss='binary_crossentropy')
model.fit(x, y, epochs=5000)
# 결과 그래프 출력
plt.scatter(x, y)
plt.plot(x, model.predict(x), 'r')
plt.show()
# 임의의 입력을 이용하여 결과를 예측해보기
t = 7
prediction = model.predict([t])
print("입력: %.f, 예상 결과: %.01f%%." % (t, prediction * 100)) # 백분율로 출력- 실행 결과
- 결과 그래프
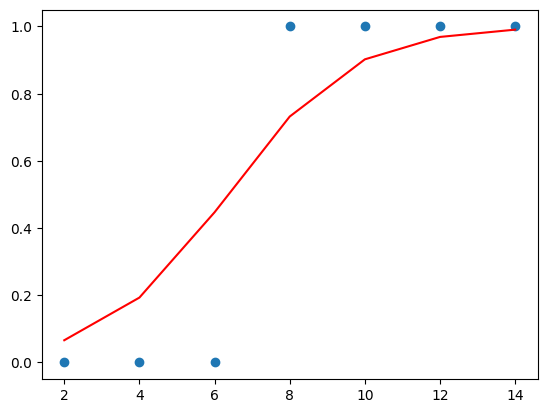
- 예측값
- 결과 그래프
Reference
- 해당 글은 "모두의 딥러닝" 6장을 기반으로 작성되었습니다.
- 조태호. 모두의 딥러닝 (개정3판). 길벗(2022)
