딥러닝 기초 #7 - 오차 역전파

OilyHand·2024년 1월 8일

딥러닝 기초

목록 보기

7/17

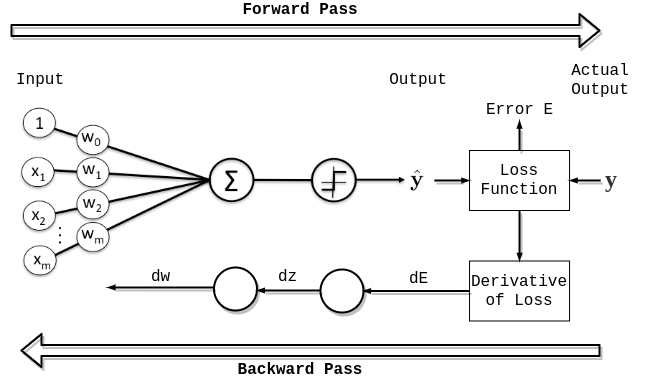
1. 오차 역전파

다층 퍼셉트론으로 XOR 문제를 해결하였지만 은닉층에 포함된 가중치를 업데이트할 방법이 없다는 문제를 직면하게 됩니다. 이는 오차 역전파(error backpropagation)라는 방법을 통해 해결되고, 이후에 딥러닝의 탄생으로 이어집니다.

1.1. 오차 역전파 기본개념

가중치를 찾는 것은 앞서 다루었던 경사 하강법을 이용하여 구할 수 있습니다. 이전에 실습했던 경사 하강법의 활용은 단일 퍼셉트론일 때 사용할 수 있습니다. 다층 퍼셉트론에서는 은닉층이 생겨 여러번의 경사 하강법을 실행해야 합니다. 다층 퍼셉트론에서 오차를 수정하는 오차 역전파의 과정은 다음과 같습니다.

오차 역전파의 과정

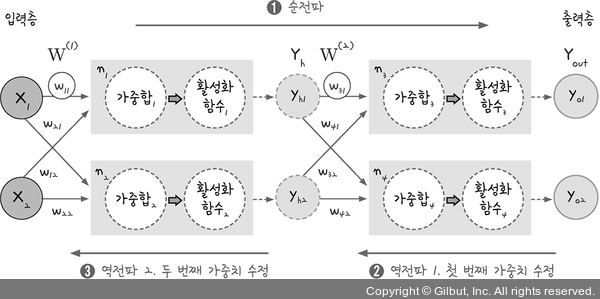
순전파
1. 입력층, 은닉층, 출력층 방향으로 한 번의 순전파 과정을 통해 결과를 계산합니다. 그 결과를 통해 오차를 계산하여 은닉층으로 값을 전달합니다.
역전파
1. 출력층으로부터 전달받은 값을 이용하여 출력층으로 값을 전달하는 노드의 가중치를 계산하여 수정합니다.
2. 출력층으로부터 전달받은 값을 이용하여 은닉층 결과에 값을 전달하는 노드의 가중치를 계산하여 수정합니다.

1.2. 오차 역전파의 계산법

1.2.1. 합성함수의 미분

다음과 같이 함수가 주어졌다고 생각해봅시다.

$y=y(x), \; x=x(t)$

위의 식을 보면 $y$ 는 $x$ 에 대한 함수이고, $x$ 는 $t$ 에 대한 함수입니다. 여기서 $y$ 는 다음과 같은 합성함수로 나타낼 수 있습니다.

$y=y(x(t))$

기존에 다루었던 미분법은 정의역에 대한 미분이었지만 여기서는 정의역의 정의역에 대한 미분이라고 볼 수 있습니다. 미분의 정의에 의해 $t$ 에 대한 $y$ 의 미분은 다음과 같이 나타낼 수 있습니다.

$\displaystyle\frac{dy}{dt}=\lim_{h\to 0}\frac{y(x(t+h))-y(x(t))}{h}$

$\quad \ \ =\displaystyle\lim_{h\to 0}\frac{y(x(t+h))-y(x(t))}{h}\cdot\frac{x(t+h)-x(t)}{x(t+h)-x(t)}$

$\quad \ \ =\displaystyle\lim_{h\to 0}\frac{y(x(t+h))-y(x(t))}{x(t+h)-x(t)}\cdot\frac{x(t+h)-x(t)}{h}$

$\quad \ \ =\displaystyle\frac{dy}{dx}\cdot\frac{dx}{dt}$

1.2.2. 출력층의 가중치 계산

1.2.3. 은닉층 가중치 계산

2. 활성화 함수

2.1. 기울기 소실 문제와 활성화 함수

델타식을 이용하여 가중치를 계산할 수 있게 되었는데, 시그모이드 함수는 미분한 최대치가 0.25이므로 곱해질 수록 0에 가까워져 은닉층의 깊이를 늘릴 수록 기울기가 소실되는 문제가 발생하게 되어 가중치를 수정하기 어려워집니다. 이를 해결하기 위해 고안된 여러 활성화 함수들이 있습니다. 이러한 함수들은 tensorflow에서 activation이라는 객체에 이름을 넣어 사용할 수 있습니다.

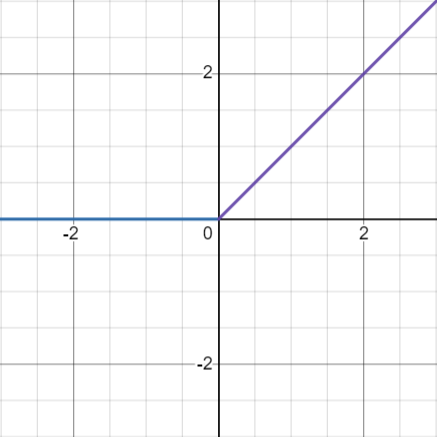
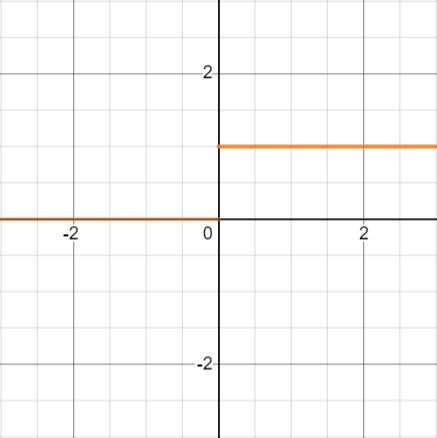
ReLU 함수
- 그래프
  
  $f(x)$ $f'(x)$
- 수식
  
  $f(x)=\begin{Bmatrix} x \quad (x>0) \\ 0 \quad (x\le0)\end{Bmatrix}$
  
  이 함수는 미분하게 되면 0 보다 작을 때는 0, 0 보다 큰 경우에는 1로 계산되므로 여러 층에 전달해도 기울기가 소실되지 않게 됩니다.

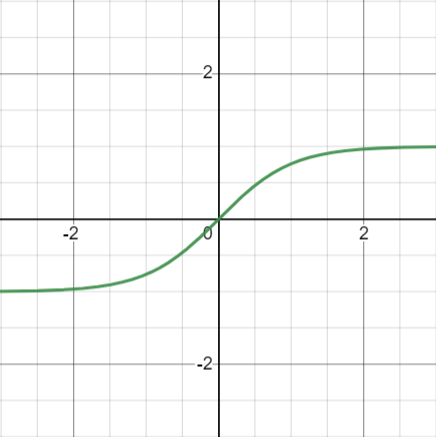
쌍곡탄젠트 함수
- 그래프
  
  $f(x)$ $f'(x)$
- 수식
  
  $f(x)=\tanh(x)$
  
  쌍곡탄젠트 함수는 시그모이드 함수와 형태는 유사하지만 미분하면 최대치가 1로 기울기 소실이 일어나지 않게 됩니다.

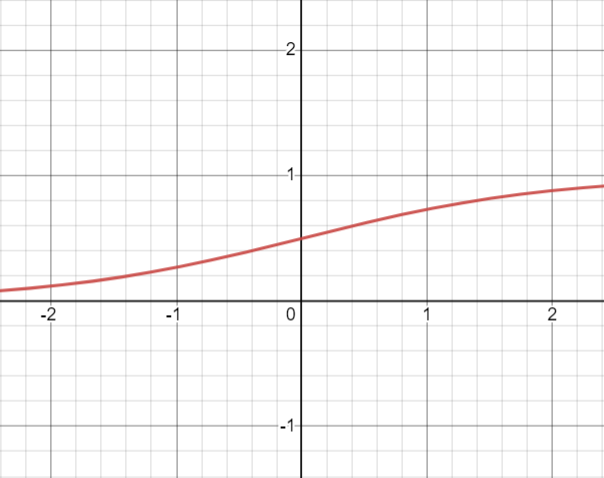
소프트플러스 함수
- 그래프
  
  $f(x)$ $f'(x)$
- 수식
  
  $f(x)=\ln(1+e^x)$
  
  ReLU 함수는 미분한 값이 0 에서 바로 0으로 잘라버리지만 소프트플러스 함수는 미분했을 때 0을 만드는 기준을 완화시킨 형태의 함수입니다.

3. 고급 경사 하강법

이전에 공부했던 경사 하강법은 계산량이 많기 때문에 이러한 점을 보완한 고급 경사 하강법들이 있습니다.

3.1. 확률적 경사 하강법

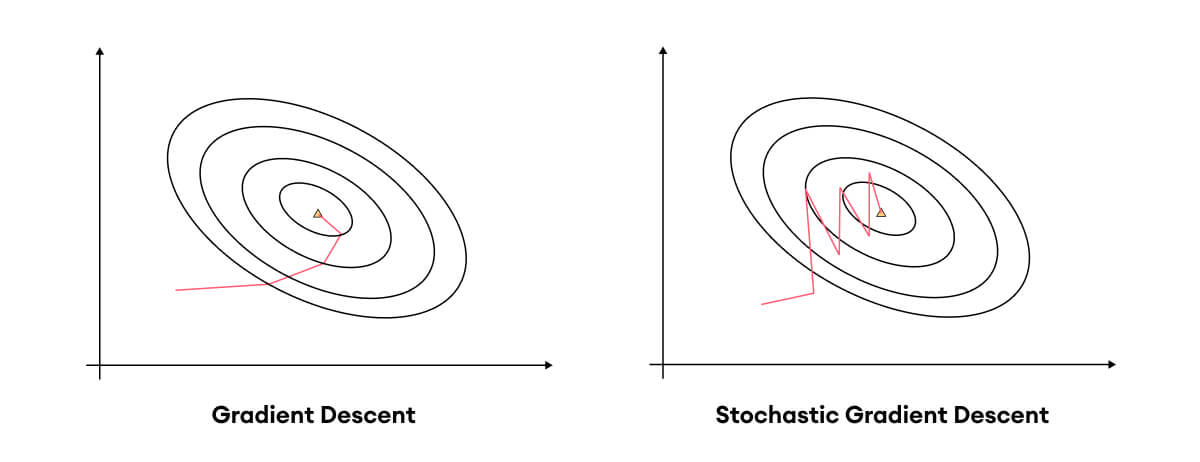
확률적 경사 하강법 (stochastic gradient descent, SGD)는 전체 데이터를 사용하지 않고 랜덤하게 샘플링된 데이터만 사용하여 빠르게 계산하는 방식의 경사 하강법입니다. 경사 하강법과 확률적 경사 하강법의 차이는 다음과 같이 비교할 수 있습니다.

3.2. 모멘텀

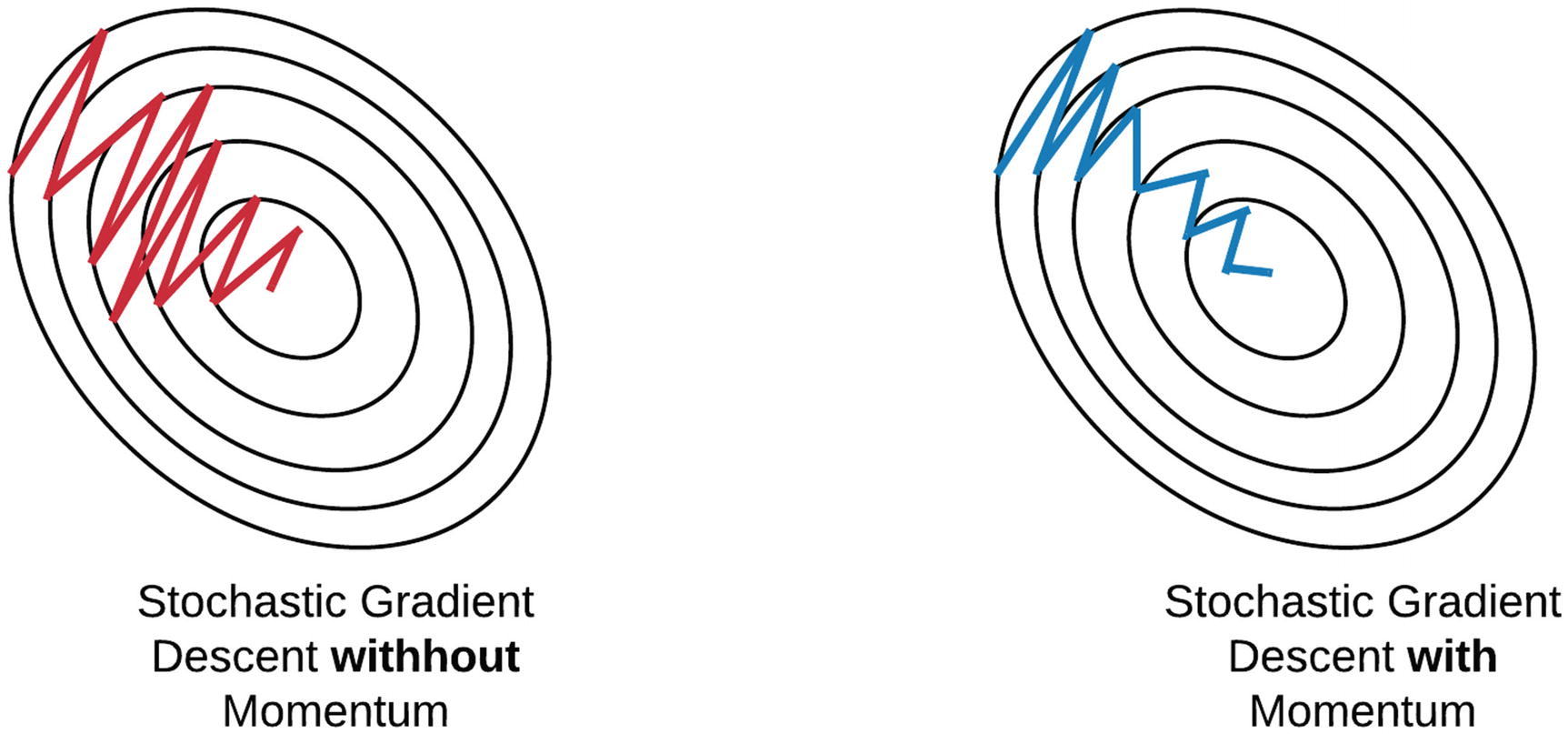
모멘텀(Momentum)은 관성이라는 뜻을 가지고 있습니다. SGD는 계산량이 적어 속도는 빠르지만 값이 불안정하게 변화하는 것을 확인할 수 있습니다. 모멘텀을 적용한다는 것은 오차를 이전에 수정한 값을 참고하여 같은 방향으로 일정한 비율만 수정되도록 하여 마치 관성이 있는 것처럼 값을 찾아내도록 구현한 알고리즘입니다.