딥러닝 기초 #6 - 퍼셉트론

OilyHand·2024년 1월 8일

딥러닝 기초

목록 보기

6/17

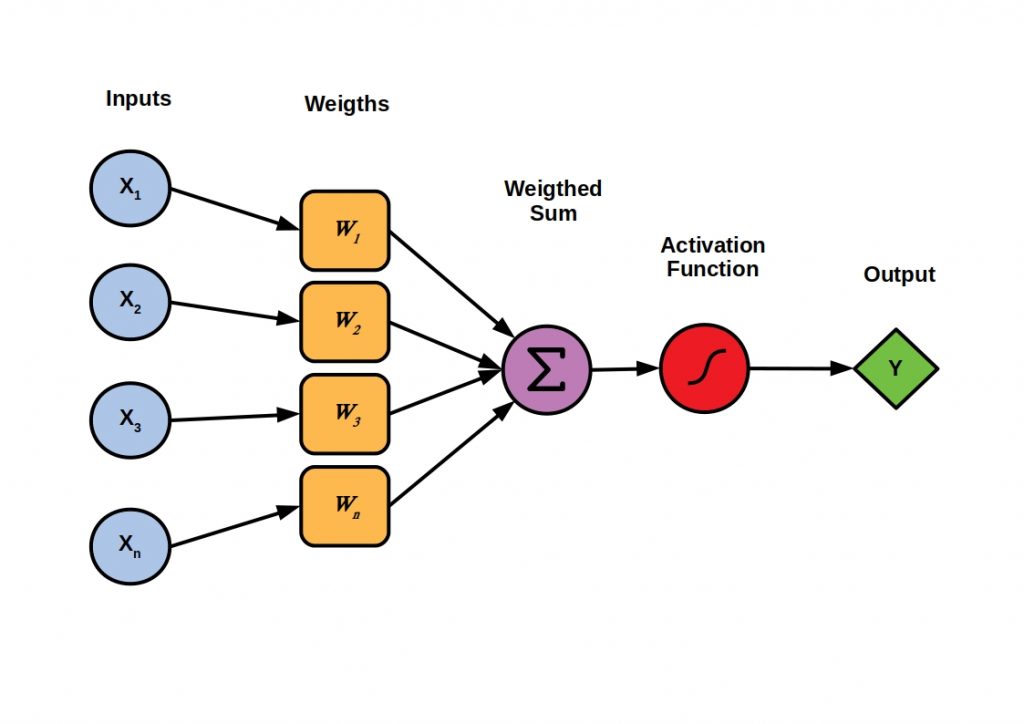
1. 퍼셉트론

1.1. 퍼셉트론의 등장

인간의 뇌는 뉴런이라는 약 1,000억 개의 신경세포로 이루어져 있습니다. 뉴런과 뉴런 사이에 있는 시냅스라는 연결 부위에서는 자극에 대한 신경전달물질을 분비하고 다음 뉴런은 그 물질에 따른 전위 변화를 일으켜 신호를 전달합니다. 이러한 인간의 신경 구조를 모방하여 마치 사람처럼 '생각'하는 지능을 구현하고자 하는 연구를 인공 신경망 연구라고 합니다. 미국의 신경생물학자 프랑크 로젠블랫이 이 개념을 퍼셉트론(perceptron)이라는 이름의 장치로 만들어 냈습니다.

퍼셉트론은 입력 값 여러 개를 받아 가중치를 조절하여 학습할 수 있도록 만들어졌습니다. 그리고 경사 하강법을 도입하여 최적의 경계선을 그릴 수 있게 한 아달라인(Adaline)이 개발됩니다. 이러한 퍼셉트론과 아달라인은 머신러닝의 중요한 알고리즘들로 발전합니다.

1.2. 퍼셉트론의 한계

경계를 나누는 선을 찾을 수 있음	경계를 나누는 선을 찾을 수 없음

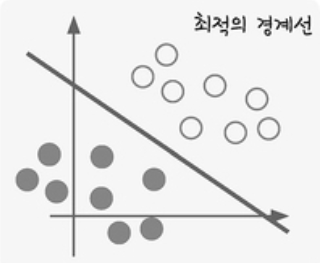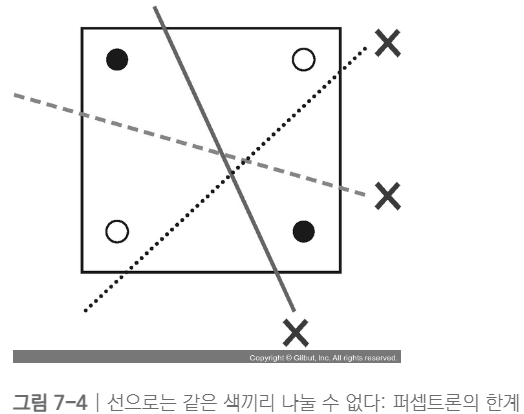퍼셉트론을 이용하면 왼쪽 그래프와 같은 경우에는 경계선을 찾을 수 있지만 오른쪽 그래프와 같이 데이터가 주어진 경우에는 경계선을 찾을 수 없다. 이러한 한계를 설명하는 문제 중 대표적으로 XOR 문제가 있다.

XOR 문제

컴퓨터와 같이 이진수를 사용할 때, 입력을 이용하여 출력을 결정하는 회로를 논리 게이트(logic gate)라고 합니다. 그 중 XOR(exclusive or) 게이트는 두 입력의 값이 다를 때 1을 출력하는 논리 게이트입니다. 결과가 0이면 흰색 점으로, 1이면 검은색 점으로 나타내어 경계선을 찾으면 다음과 같은 그래프를 생각해볼 수 있습니다.

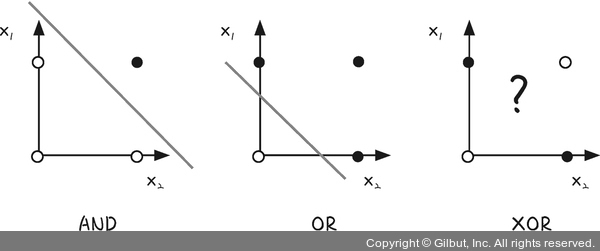
이러한 퍼셉트론의 한계는 다층 퍼셉트론, 오차 역전파가 개발되면서 해결됩니다.

2. 다층 퍼셉트론

2.1. 은닉층(hidden layer)

앞서 살펴봤던 퍼셉트론의 한계는 2차원 평면에서 3차원 공간으로 생각을 확장시켜 문제를 해결할 수 있었습니다. 다음과 같이 평면을 휘어 주어 안 보이는 부분을 만들어 경계선을 그릴 수 있습니다. 이렇게 안 보이는 부분을 만드는 것을 은닉층(hidden layer)을 만든다고 하고, 이러한 은닉층을 사용하여 퍼셉트론 두 개를 한 번에 계산하면 여러 직선을 얻을 수 있습니다.

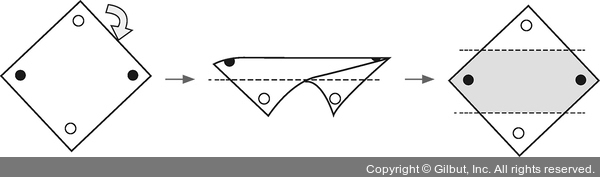
2.2. 은닉층을 이용한 XOR 문제 해결

XOR 게이트는 다음과 같이 여러 논리 게이트를 이용하여 같은 출력 결과를 얻을 수 있도록 나타낼 수 있습니다.

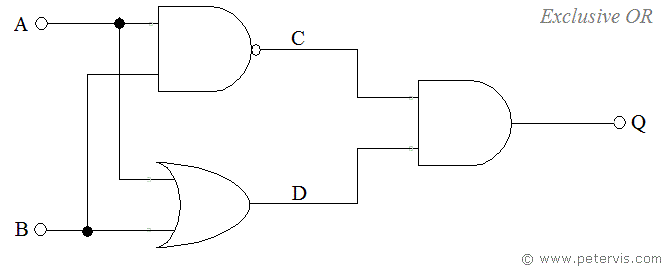
해결 과정

입력 A, B를 각각 게이트로 보냅니다.
첫번째 연산에서는 NAND(왼쪽 상단 게이트) 처리를 합니다.
이와 동시에 두 번째 연산에서 OR(왼쪽 하단 게이트) 처리를 합니다.
2-3을 통해 구한 결괏값 C, D를 AND(오른쪽 게이트) 처리하여 최종 출력 값 Q를 구합니다.

위의 과정에서 2-3을 은닉층이라 볼 수 있습니다.

2.3. 다층 퍼셉트론의 설계

은닉층을 이용하는 다층 퍼셉트론의 구조는 다음과 같습니다.

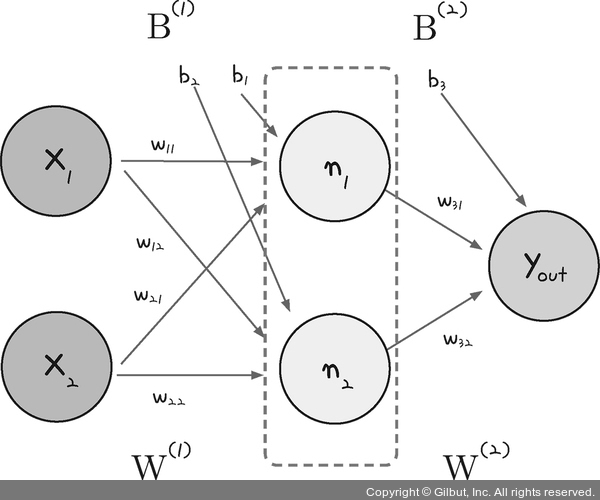
점선으로 표시된 부분이 은닉층으로, 실행할 때는 입력 $x_1$ , $x_2$ 에서 가중치( $w$ )를 곱하고 편향( $b$ )을 더하여 은닉층으로 전송합니다.
은닉층에서는 값이 모이는 중간 정거장에 해당하는 노드(node) $n_1$ , $n_2$ 에 취합되어 활성화 함수를 통해 다음으로 보내집니다.

2.4. 다층 퍼셉트론을 이용한 XOR 문제 해결

이진 논리 구조를 다루므로 활성화 함수는 시그모이드 함수( $\sigma(x)$ )를 이용합니다. 시그모이드 함수를 이용하여 노드를 다음과 같이 나타낼 수 있습니다.

$n_1=\sigma(x_1 \cdot w_{11} + x_2 \cdot w_{12} + b_1)$

$n_2=\sigma(x_1 \cdot w_{21} + x_2 \cdot w_{22} + b_2)$

이를 이용하여 결과 $y_{out}$ 은 다음과 같은 식으로 나타낼 수 있습니다.

$y_{out}=\sigma(n_1 \cdot w_{31} + n_2 w_{32} + b_3)$

각각의 가중치와 편향은 2차원 배열을 이용하여 다음과 같이 표시할 수 있습니다.

$W^{(1)}=\begin{bmatrix}w_{11}&w_{12}\\w_{21}&w_{22}\\ \end{bmatrix} \qquad W^{(2)}=\begin{bmatrix} w_{31} \\ w_{32} \end{bmatrix}$

$B^{(1)}=\begin{bmatrix} b_1\\ b_2 \end{bmatrix} \qquad B^{(2)}=\begin{bmatrix} b_3 \end{bmatrix}$

예제로는 다음과 같이 가중치와 편향을 정하여 XOR 문제를 해결해보도록 하겠습니다.

$W^{(1)}=\begin{bmatrix} -2 & 2 \\ -2 & 2 \\ \end{bmatrix} \qquad W^{(2)}=\begin{bmatrix} 1 \\ 1 \end{bmatrix}$

$B^{(1)}=\begin{bmatrix} 3 \\ -1 \end{bmatrix} \qquad B^{(2)}=\begin{bmatrix} -1 \end{bmatrix}$

3. Python을 이용한 다층 퍼셉트론

3.1. 실습 코드

앞서 다룬 예제를 이용하여 다층 퍼셉트론을 다음과 같이 파이썬 코드로 작성해볼 수 있습니다.

import numpy as np

# 1. 가중치와 편향 입력
w11 = np.array([-2, -2])
w12 = np.array([2, 2])
w2 = np.array([1, 1])
b1 = 3
b2 = -1
b3 = -1

# 1. 퍼셉트론 함수 정의
def MLP(x, w, b):
    y = np.sum(w * x) + b
    if y <= 0:
        return 0
    else:
        return 1

# NAND 게이트
def NAND(x1, x2):
    return MLP(np.array([x1, x2]), w11, b1)

# OR 게이트
def OR(x1, x2):
    return MLP(np.array([x1, x2]), w12, b2)

# AND 게이트
def AND(x1, x2):
    return MLP(np.array([x1, x2]), w2, b3)

# XOR 게이트
def XOR(x1, x2):
    return AND(NAND(x1, x2), OR(x1, x2))

# x1 값, x2 값을 번갈아 대입하며 최종 값 출력
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
    y = XOR(x[0], x[1])
    print("입력 값: " + str(x) + " 출력 값: " + str(y))