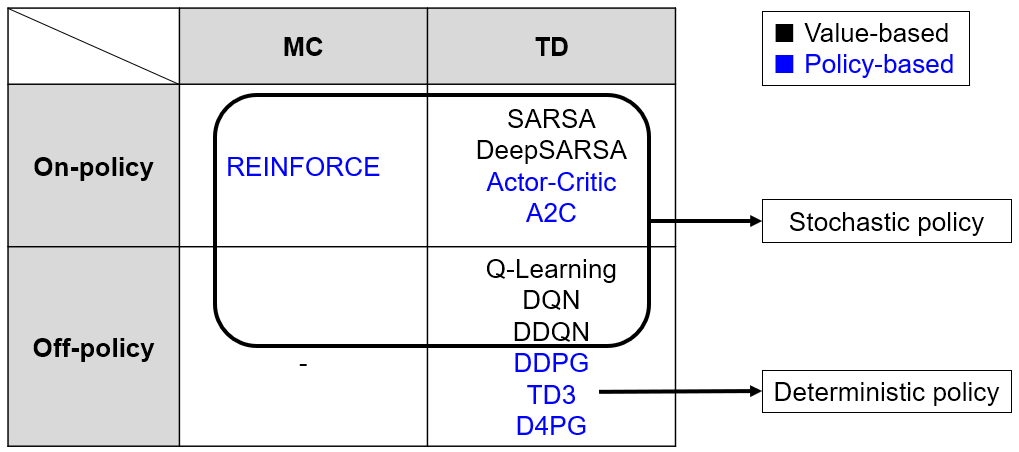
Reinforcement Learning Summary

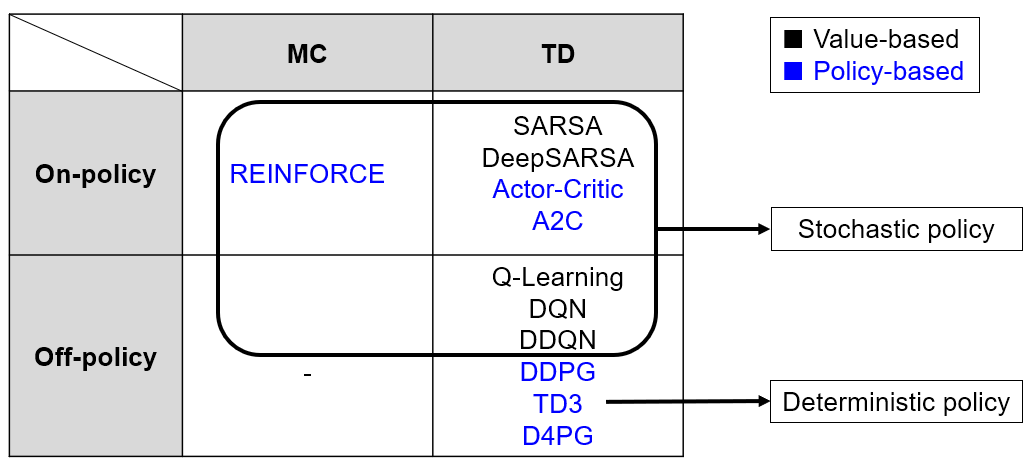
Reinforcement Learning

Reinforcement Learning(RL)이 풀고자 하는 문제는 Sequential Decision Problem(SDP)

Sequential Decision Problem(SDP)

• SDP는 여러번의 선택을 순차적으로 진행하는 문제
• SDP의 목적은 보상의 총 합을 최대화 하는 것

• Agent
  • 환경을 관찰
  • 행동을 선택
• Environment
  • Agent를 제외한 나머지
  • Agent에게 적절한 보상을 부여

구성 요소

• State
  • 현재 agent의 정보로, environment로 부터 관찰
• Action
  • Agent가 특정 상태에서 취할 수 있는 행동
• Reward
  • Agent가 학습할 수 있는 유일한 정보
  • Reward를 통해 agent는 자신이 수행한 action을 평가
  • Reward는 environment의 일부로, agent가 action을 수행하기 전에는 알 수 없음
• Policy
  • SDP에서 구해야 할 답
  • 각 state에서 수행할 action
  • Optimal policy : Reward가 최대가 되는 policy
    • SDP가 풀렸다는 것은 optimal policy를 구했다는 의미

Markov Decision Process(MDP)

• SDP를 컴퓨터가 이해할 수 있도록 수학적으로 재정의한 것
• MDP의 목적 또한 reward를 최대화 하는 것
• Agent는 stochastic하게 action를 선택
• Agent의 action에 따라 next state와 reward가 결정

Markov Property

• 미래는 현재로부터만 정해지며, 과거는 영향을 주지 못함
• State $S_t$ is "Markov" if and only if
  $P[S_{t+1}|S_t]=P[S_{t+1}|S_1,S_2,\cdots ,S_t]$

구성 요소

$\{ S, A, P_{ss'}^a, R_s^a, \gamma \}$

• $S$ : State의 집합
• $A$ : Action의 집합
• $P_{ss'}^a$ : State transition probability
  • $P_{ss'}^a=P[S_{t+1}=s'|S_t=s, A_t=a]$
  • State transition probability를 알면 'Model-based'
    • Dynamic Programming을 적용
  • State transition probability를 모르면 'Model-free'
    • Reinforcement Learning을 적용
• $R_s^a$ : Reward
  • $R_s^a=E[R_{t+1}|S_t=s, A_t=a]$
  • 같은 state $s$에서 같은 action $a$를 수행하더라도 reward가 다를 수 있으므로 expectation 형태로 표현
  • Reward는 현재 시간 $t$가 아닌, $t+1$에 environment로 부터 받음
• $\gamma$ : Discount factor
  • $\gamma \in [0, 1]$
  • Why use discounted rewards?
    • Cyclic MDP에서 infinite reward를 피하기 위해
    • 미래의 uncertainty를 완벽히 표현 불가능하므로
    • Financial reward 같은 경우 동일한 reward의 경우 당장 받는 것이 먼 미래에 받는 것 보다 가치가 크므로
    • 즉각적인 보상을 선호하는 human/animal behavior에 의해
  • 현재 시간 $t$로 부터 $k$만큼 지난 후 받은 reward의 가치는 $\gamma ^{k-1}R_{t+k}$
    • $\gamma$가 0에 가까울 수록 'short-sighted'
    • $\gamma$가 1에 가까울 수록 'far-sighted'
  • Discount factor로 인해, agent는 같은 보상을 받더라도 더 빠른 보상을 받는 쪽을 선택하게 됨

Episode

• Agent가 겪는 처음부터 마지막까지의 state trajectory
  $S_1, S_2, S_3,\cdots ,S_{T-1}, S_T$
• $s_1 \rightarrow a_1 \rightarrow s_2 \rightarrow a_2 \rightarrow \cdots \rightarrow s_T$ 식으로 state와 action이 번갈아가며 진행

Policy

• 각 state에서 수행할 action
  $\pi(a|s)=P[A_t=a|S_t=s]$
• Stochastic policy : 각 state에서 stochastic하게 action을 선택
• Deterministic policy : 각 state에서 선택할 action이 정해져 있음
  • Optimal policy는 deterministic policy

Return

• 현재 시간 $t$로 부터 episode 종료까지 받을 reward들의 현재 가치의 합
  $G_t=R_{t+1}+\gamma R_{t+2}+\gamma ^2 R_{t+3}+\cdots + \gamma ^{T-1}R_{t+T}=\sum_{k=0}^{T-1} \gamma^{k} R_{t+k+1}$

Value function

• Return에 대한 기댓값(expectation)

• State value function
  • 특정 state에 있을 때 앞으로 받을 return의 기댓값
  • 특정 state가 얼마나 좋은지를 나타냄
    $v_{\pi}(s)=E_{\pi}[G_t|S_t=s]$
• Action value function(Q Function)
  • State $s$에서 action $a$를 선택했을 때 앞으로 받을 return의 기댓값
  • 특정 state에서 각 action이 얼마나 좋은지를 나타냄
    $q_{\pi}(s,a)=E_{\pi}[G_t|S_t=s, A_t=a]$

Bellman Equation

Bellman Expectation Equation

• 현재 state $S_t$와 next state $S_{t+1}$의 value function 간의 관계식
  • Bellman expectation equation을 반복하여 풀면 optimal value function을 구할 수 있음

• For state value function
  $v_{\pi}(s)=E_{\pi}[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_t=s]$
• For action value function(Q Function)
  $q_{\pi}(s,a)=E_{\pi}[R_{t+1}+\gamma q_{\pi}(S_{t+1}, A_{t+1})|S_t=s, A_t=a]$
  $q_\pi(s,a)=R_s^a+\gamma v_\pi(s')$

• State value function과 action value function간의 관계
  $v_{\pi}(s)=\sum_{a \in A} \pi(a|s)q_{\pi}(s,a) =\sum_{a \in A} \pi(a|s)\left( R_s^a+\gamma \sum_{s' \in S}P_{ss'}^a v_{\pi}(s')\right)$
  • State $s$의 가치는 해당 state에서 선택할 수 있는 모든 action들의 가치들의 합

Optimal value function

• Return의 최댓값

• Optimal state value function
  $v^*(s)=\max _{\pi}[v_{\pi}(s)]$
• Optimal action value function(Q Function)
  $q^*(s,a)=\max _{\pi}[q_{\pi}(s,a)]$
  • Optimal policy -> Optimal Q function

Optimal policy

• Reward가 최대가 되는 policy
  $\pi^*(a|s)=\argmax _{a \in A}[q^*(s,a)]$
  $\pi^*(a|s)= \begin{cases} 1, \;if\;a=\argmax _{a \in A}q^*(s,a)\\ 0, \;else \end{cases}$
• 가능한 action 중 최고의 Q function을 선택 : Greedy policy
• Optimal policy를 구하는 것이 목적

Bellman Optimality Equation

• For state value function
  $v^*(s)=\max _a[q^*(s,a)|S_t=s] =\max _a E[R_{t+1}+\gamma v^*(S_{t+1})|S_t=s]$
• For action value function(Q Function)
  $q^*(s,a)=E[R_{t+1}+\gamma \max _{a'}q^*(S_{t+1},a')|S_t=s, A_t=a]$

Dynamic Programming

• 'Model-based' MDP를 계산을 통해 푸는 방법
• Environment에 대한 정보를 알기 때문에 optimal policy를 계산

Policy Iteration

• Policy evaluation과 policy improvement를 반복적으로 수행
• Explicit policy : Policy와 value function이 분리
• 가장 높은 보상을 얻는 정책을 구하는 것이 목적

• Policy evaluation
  • Bellman expectation equation을 반복적으로 계산
    $v_{k+1}(s)=\sum _{a \in A} \pi (a|s)\left (R_s^a+\gamma v_k(s') \right)$

• Policy improvement
  • State $s$에서 가장 큰 Q function을 가지는 action을 선택(greedy)
    $\pi'(s)=\argmax _{a \in A} q_{\pi}(s,a)$

Value Iteration

• 현재의 value function이 optimal하다고 가정
• 현재의 value function에 deterministic policy를 적용
• Implicit policy : Policy가 value function에 내재되어 있어, value function을 update하면 policy 또한 자동으로 발전
• Policy improvement가 필요 없음
  • Optimal value function을 가정했으므로, Bellman optimality equation을 반복적으로 계산하면 optimal value function, optimal policy가 구해짐
    $v_{k+1}(s)=\max _a[R_s^a+\gamma v_k(s')]$
    $\pi^*(s)=\argmax _{a \in A}E[R_s^a+\gamma v_k(s')]$

Limitation

• Environment($R_s^a, P_{ss'}^a$)를 정확히 알아야 하지만, real-world problem들은 이들을 정확히 알기 어려움
• 모든 value function을 계산해야 하므로, MDP의 크기가 조금만 커져도 계산에 시간이 굉장히 많이 소요됨

Reinforcement Learning

• 'Model-free' MDP를 학습을 통해 푸는 방법
• Environment를 모르기 때문에 'trial and error'로 optimal policy를 학습

Monte Carlo Approximation

• Sampling : Agent가 episode를 한번 진행하는 것
  • Sample들의 평균으로 value function을 estimate
    $v_{\pi}(s) \approx \frac {1}{N(s)} \sum_{i=1}^{N(s)}G_i(s)$
• Expected return : $v_{\pi}(s)$
• Empirical return : $V(s)$
  • $\lim_{N \to \infty} V(s)=v_{\pi}(s)$
    $V(S_t)\leftarrow V(S_t)+\alpha (G_t-V(S_t))$
• MC는 episode가 끝나야 학습 가능

Temporal Difference Prediction

• Episode가 끝날때까지 기다리지 않고 time step마다 value function을 update
  $V(S_t)\leftarrow V(S_t)+\alpha (R_{t+1}+\gamma V(S_{t+1})-V(S_t))$
• Episode가 끝나지 않아 $G_t$를 모르므로, 이를 $R_{t+1}+\gamma V(S_{t+1})$로 대체
• TD는 episode가 끝나지 않아도 학습 가능

MC vs TD

• TD의 경우 MC에 비해 update target이 biased 되어있고, variance가 낮음
  • TD는 update target이 하나의 state, action, reward의 영향을 받지만, MC의 경우 다수의 state, action, reward의 영향을 받으므로

SARSA

• TD 기반 알고리즘
  • TD는 state value function을 update
  • SARSA는 action value function(Q Function)을 update
    - Bellman expectation equation 기반
    $Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha (R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t))$
• $\epsilon$-greedy policy
  $\pi(s)=\begin{cases} a^*=\argmax _{a \in A}Q(s,a), \;1-\epsilon \\ random, \;\epsilon \end{cases}$
• 위의 식대로 Q function을 update하기 위해 $[S_t,A_t,R_{t+1},S_{t+1},A_{t+1}]$ sampling

Algorithm

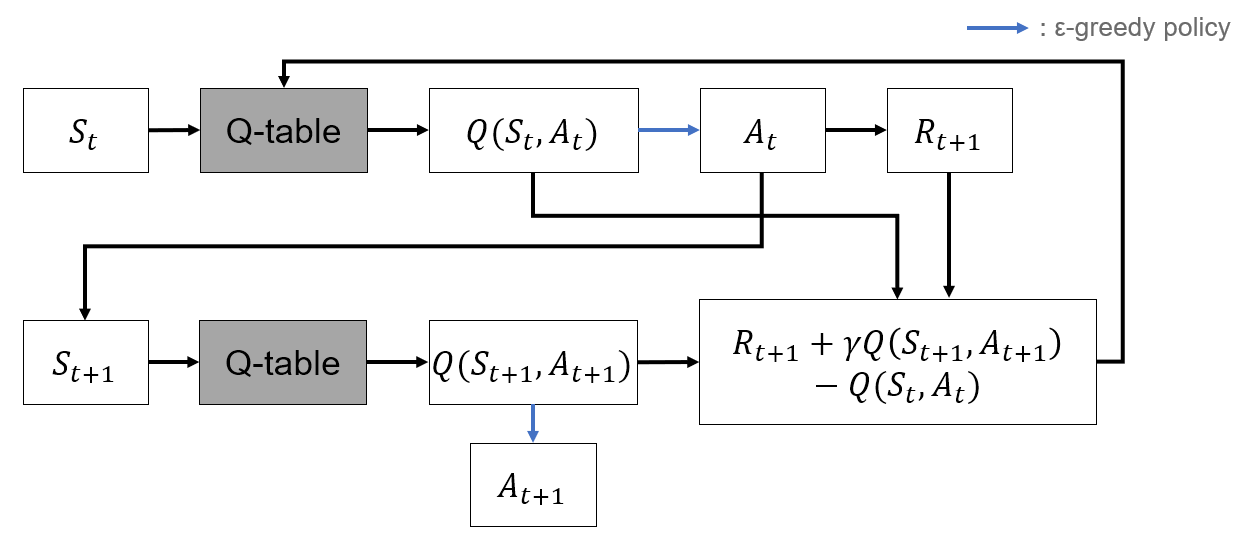
1. $\epsilon$-greedy policy로 $[S_t,A_t,R_{t+1},S_{t+1},A_{t+1}]$ sample
2. 획득한 sample을 통해 Q function update

• On-Policy : Agent의 행동에 따라 학습
• $\epsilon$-greedy policy 때문에 잘못된 policy를 학습하거나, agent가 특정 state에 갇히는 문제

Q Learning

• SARSA의 단점을 보완
  • Off-Policy : 행동하는 policy와 학습하는 policy를 분리
    - 행동은 $\epsilon$-greedy하게 선택
    - Q function은 greedy하게 update
    - Bellman optimality equation 기반
    $Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha (R_{t+1}+\gamma \max _{a' \in A}Q(S_{t+1},a')-Q(S_t,A_t))$
• 위의 식대로 Q function을 update하기 위해 $[S_t,A_t,R_{t+1},S_{t+1}]$ sampling

Algorithm

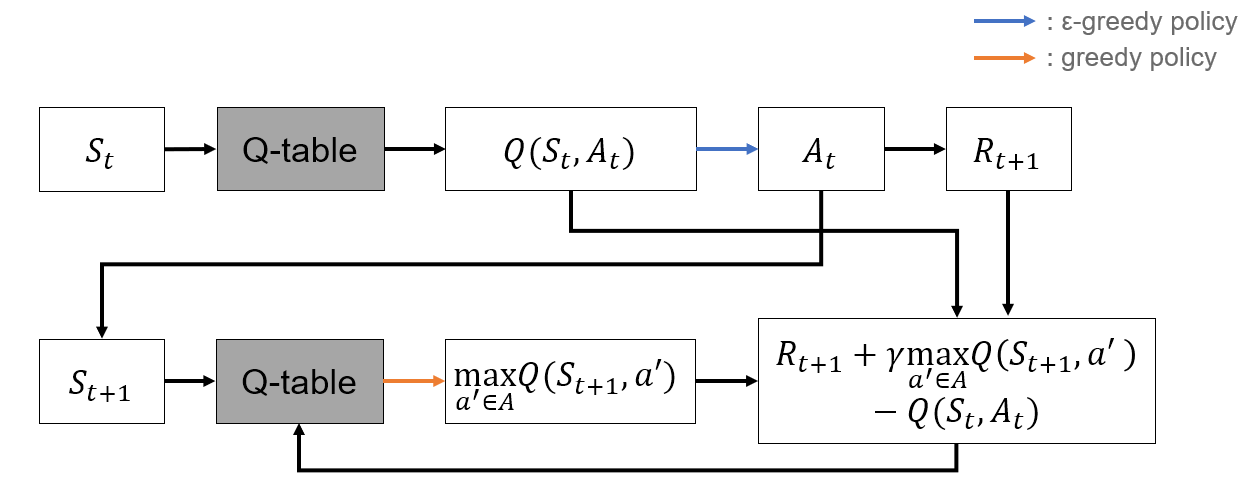
1. $\epsilon$-greedy policy로 $[S_t,A_t,R_{t+1},S_{t+1}]$ sample
2. 획득한 sample을 통해 Q function update

Limitations of Classic RL

• 모든 state의 Q function을 저장해야 함
• Q function을 해당 state에 방문할 때 마다 update
• 간단하거나 time-invariant한 environment에만 적용 가능

Function approximation

• 방문한 state의 Q function을 기반으로 비슷한 state들의 Q function은 approximate
• Function approximation method는 다양하지만 대부분 neural network를 사용
• Q function을 parameter $\theta$로 approximate
  $q_{\theta}(s,a)\approx q_{\pi}(s,a)$
• Supervised-learning으로 parameter $\theta$를 학습

DeepSARSA

Algorithm

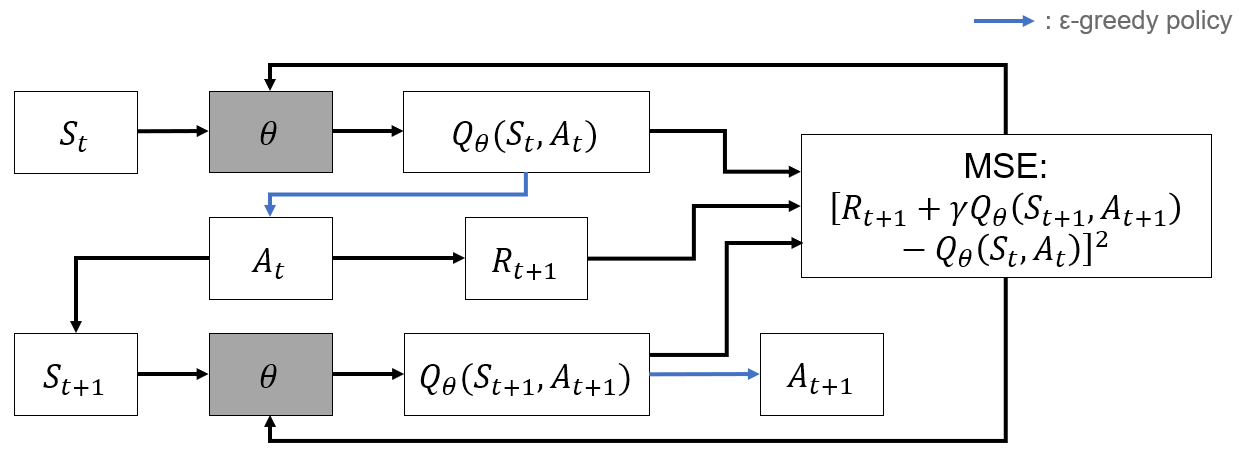
1. NN을 통해 Q function 근사 : $q_{\theta}$(s,a)
2. $\epsilon$-greedy policy로 action 선택
3. Action 수행 후 $S_{t+1},R_{t+1}$ sample
4. 획득한 sample로 NN parameter update

Q Learning w/ Func. Approx.

Algorithm

1. NN을 통해 Q function 근사 : $q_{\theta}(s,a)$
2. $\epsilon$-greedy policy로 action 선택
3. Action 수행 후 $S_{t+1},R_{t+1}$ sample
4. 획득한 sample로 NN parameter update

DQN(Deep Q Network)

• "Playing Atari with Deep Reinforcement Learning(2013) - DeepMind"

• Off-Policy
• Experience Replay
  • TD update target이 biasd, low variance인 문제 해결 위함
  • FIFO 형식의 replay memory 적용
  • Replay memory에 매 time step 마다 $[S_t, A_t, R_{t+1}, S_{t+1}]$ 저장
  • 매 time step 마다 replay memory에서 mini-batch를 random sample하며, mini-batch로 NN parameter update
  • Sample들의 correlation이 없어 NN의 안정적인 학습 가능
• Target Network
  • NN을 하나만 사용할 경우 NN의 output과 target인 $Q(S_{t+1},a'), Q(S_t, A_t)$이 같은 NN에서 얻어지므로 학습이 불안정
  • Action을 선택하는 NN과 update target를 구하는 NN을 분리
    • Action network : $\theta$
      • $Q(S_t,A_t)=q_\theta(s,a)$
    • Target network : $\theta^-$
      • $Q(S_{t+1},a')=q_{\theta ^-}(s,a')$
  • 두 Q function이 크게 달라지는 것을 막기 위해 일정 time step마다 $\theta^-$를 $\theta$로 update

Algorithm

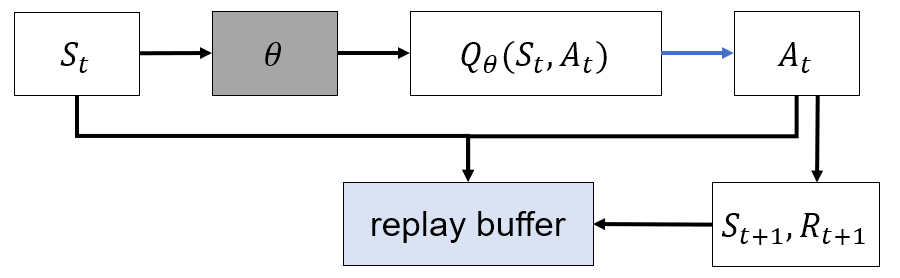
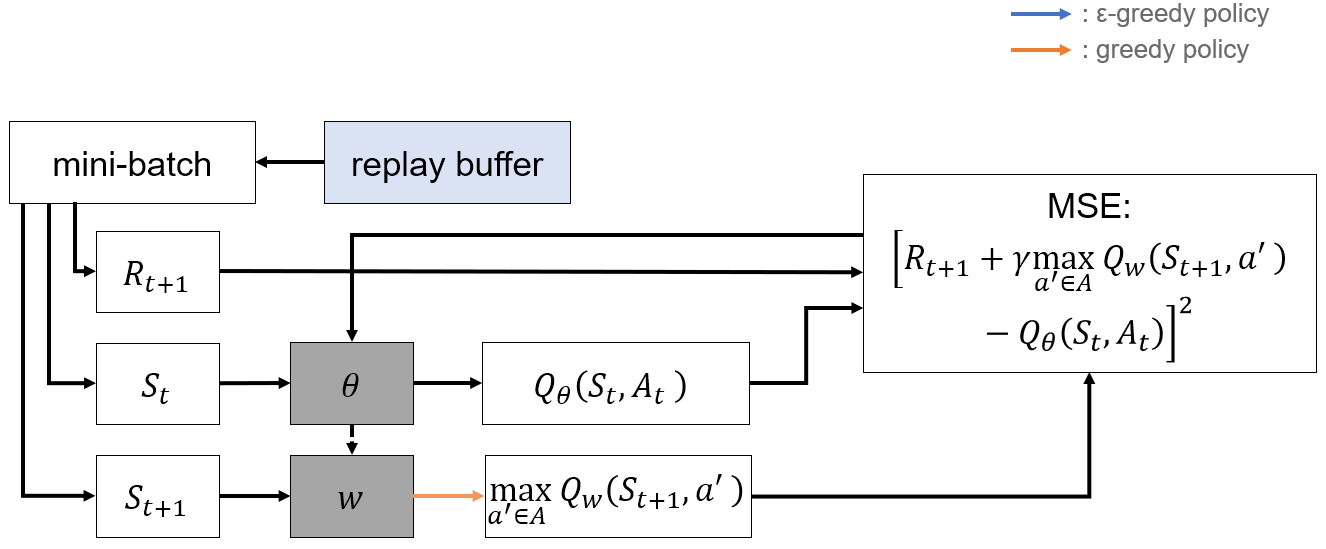
1. Action network로 q function 근사 : $q_{\theta}(s,a)$
2. $\epsilon$-greedy policy로 action 선택
3. Action 수행 후 $R_{t+1},S_{t+1}$ sample
4. Replay memory에 $[S_t, A_t,R_{t+1},S_{t+1}]$ 저장
5. 충분한 sample이 모였을 경우, replay memory에서 무작위로 mini-batch를 sampling
6. Target network로 update target 생성 후, mini-batch로 action network update
7. 일정 time step마다 action network parameter를 target network parameter로 복사

Policy Gradient

• 기존의 RL은 value-based
  • Agent는 value function을 기반으로 action을 선택하고, value function을 update하며 학습
  • NN이 Q function을 approximate
• Policy-based
  • Value function을 기반으로 action을 선택하지 않고 policy를 직접적으로 approximate
  • NN이 policy를 approximate
    • state $\rightarrow$ NN $\rightarrow$ policy

• Policy
  $\pi_\theta(a|s)=P[A_t=a|S_t=s, \theta]\approx \pi(a|s)$
• Policy objective function
  $J(\theta)=E[R_1+\gamma R_2+\cdots +\gamma^{T-1}R_T|\pi_\theta]$
  • $J(\theta)$를 maximize하는 것이 목표
• Policy Gradient
  $\nabla_\theta J(\theta)=E_{\pi_\theta}[\nabla_\theta \log \pi_\theta (a|s)q_\pi(s,a)]$
  • NN은 policy만을 approximate하기 때문에 Q function의 값을 알 수 없어 위의 식을 바로 적용할 수 없는 문제점이 존재

REINFORCE

• MC, policy gradient based
• On-policy
• $q_\pi(s,a)$를 $G_t$로 대체
  $\nabla_\theta J(\theta)=E_{\pi_\theta}[\nabla _\theta \log \pi_\theta(a|s)G_t]$
  $c.f. \;\; q_\pi(s,a)=E[G_t|S_t=s,A_t=a]$
• MC 기반이기에 update target의 variance가 크고, episode가 끝나야 학습이 가능한 단점이 존재

Algorithm

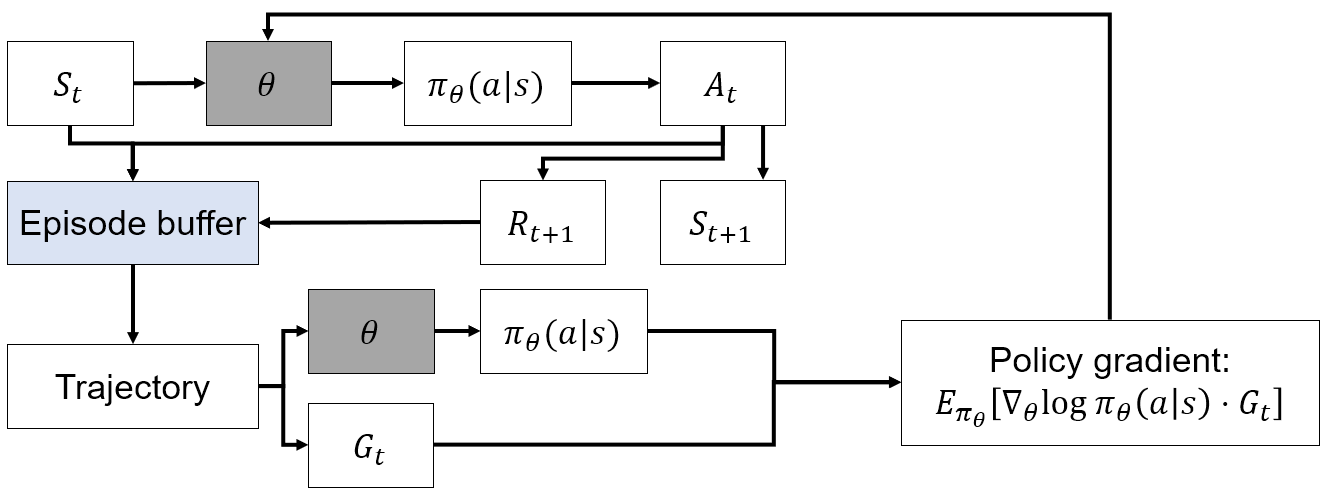
1. NN으로 policy를 구하고, policy를 따라 action 선택
2. Episode의 trajectory를 저장
   $\tau=s_0,a_0,r_1,s_1,a_1,r_2,\cdots,s_T$
3. Episode가 끝나면 $G_t$ 계산
4. Policy gradient를 계산하여 NN update

Actor-Critic

• TD, policy gradient based
• On-policy
• $q_\pi(s,a)$를 NN으로 approximate

• Actor : policy를 approximate($\pi_\theta(a|s)$)
  • parameter $\theta$
• Critic : Q function을 approximate($q_w(s,a)\approx q_\pi(s,a)$)
  • parameter $w$
  • Critic은 보통 SARSA의 방식과 유사하게 update
    $Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha (R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t))$
• Policy gradient
  $\nabla_\theta J(\theta)\approx E_{\pi_\theta}[\nabla _\theta \log \pi_\theta(a|s)\cdot q_w(s,a)]$

• $q_w(s,a)$가 NN의 output이므로, 이 값에 따라 poligy gradient가 크게 변화하여 variance가 높아지는 문제점이 존재

Algorithm

1. NN으로 policy를 구하고, policy를 따라 action 선택
2. Actor와 critic의 loss로 부터 policy gradient를 계산하여 NN update

A2C(Advantage Actor-Critic)

• Policy gradient의 variance를 낮추기 위해 Q function 대신 advantage function 사용

  $A(S_t,A_t)=Q_w(S_t,A_t)-V_v(S_t)$
  $\nabla_\theta J(\theta) \approx E_{\pi_\theta}[\nabla_\theta \log \pi_\theta (a|s) \cdot (q_w(s,a)-v_\pi(s))]$

• 위 식을 바로 사용할 경우 Critic은 $Q_w(S_t,A_t), V_v(S_t)$를 따로 approximate해야 하므로 비효율적이기 때문에 Q function을 value function으로 표현

  $c.f. \;\; q_\pi(s,a)=R_s^a+\gamma v_\pi(s')$

• Actor-Critic은 sample variance가 높아 expectation을 1개의 sample로 대체하여 사용했는데, A2C는 advantage function을 사용함에 따라 sample variance가 낮아져 N개의 sample을 사용

• TD error : Loss function for Critic

  $\delta_v=R_{t+1}+\gamma V_v(S_{t+1})-V_v(S_t)$

• Policy Gradient : Loss function for Actor

  $\nabla_\theta J(\theta)\approx E_{\pi_\theta}[\nabla _\theta \log \pi_\theta(a|s)\cdot \delta_v]$

Algorithm

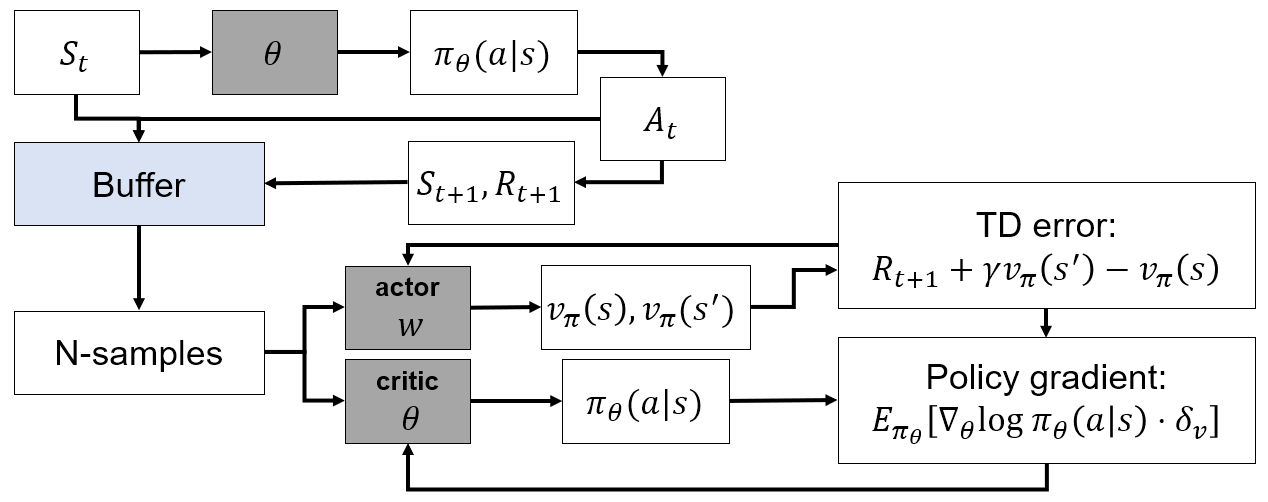
1. NN으로 policy를 구하고, policy를 따라 action 선택
2. N개의 time step의 trajectory를 저장
3. N개의 sample로 policy gradient를 계산하여 NN update

DDPG(Deep Deterministic Policy Gradient)

• Deterministic policy gradient 기반 actor-critic algorithm
• Off-policy
  • Replay buffer 사용
• Continuous action space
• 기존 algorithm들은 stochastic policy를 사용하였지만, DDPG는 deterministic policy를 사용
  • 각 state에서의 action이 정해져 있음
  • Deterministic policy이기 때문에 exploration이 부족할 수 있으므로 action에 noise를 추가
    • 대부분 OU noise 사용
• Actor와 Critic 모두 target network 사용
  • DQN과 달리 target network를 soft update
    $\theta^- \leftarrow \tau \theta+(1-\tau)\theta^-$
    $w^- \leftarrow \tau w+(1-\tau)w^-$
• 기존 reward는 $s_t, a_t$가 정해지면 다음 time step $t+1$에 받았지만, DDPG에서는 $s_t, a_t$가 정해지는 즉시 reward가 결정됨

• Actor : Action을 직접 approximate($a_{\theta, t}$)
  • parameter $\theta, \theta^-$
• Critic : Q function을 approximate($q_w(s, a_{\theta})$)
  • parameter $w, w^-$

• Policy gradient
  $\nabla_{\theta}J(\theta) \approx E_{a_\theta}[\nabla_{a_\theta}q_w(s,a_\theta)]$

Algorithm

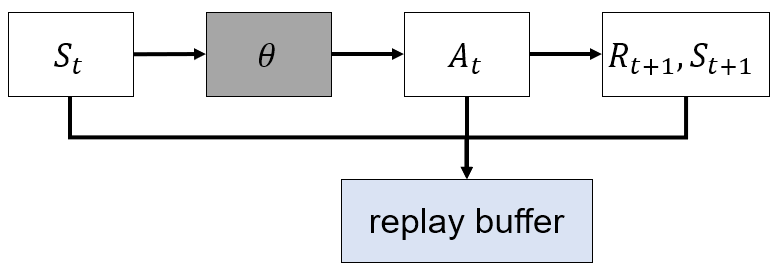
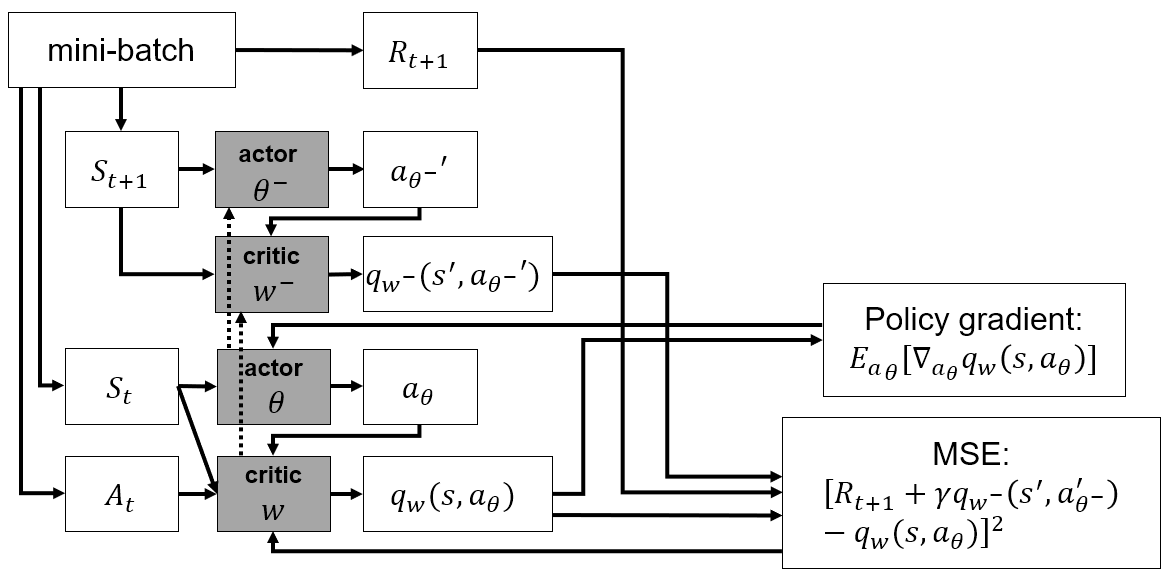
1. NN으로 action $a_{\theta,t}$선택
2. Deterministic policy이므로 exploration이 부족할 수 있기 때문에 noise를 추가하여 $a_{\theta, t}+\mathcal{N}_t$ 사용
3. Action 수행 후 $R_t, S_{t+1}$ sample
4. Replay memory에 $[S_t, A_t, R_t, S_{t+1}]$ 저장
5. 충분한 sample이 모였을 경우, replay memory에서 무작위로 mini-batch를 sampling
6. Target network로 update target 생성 후, mini-batch로 network update
7. 매 time step마다 network parameter $\theta, w$를 soft update

DDQN(Double Deep Q-Network)

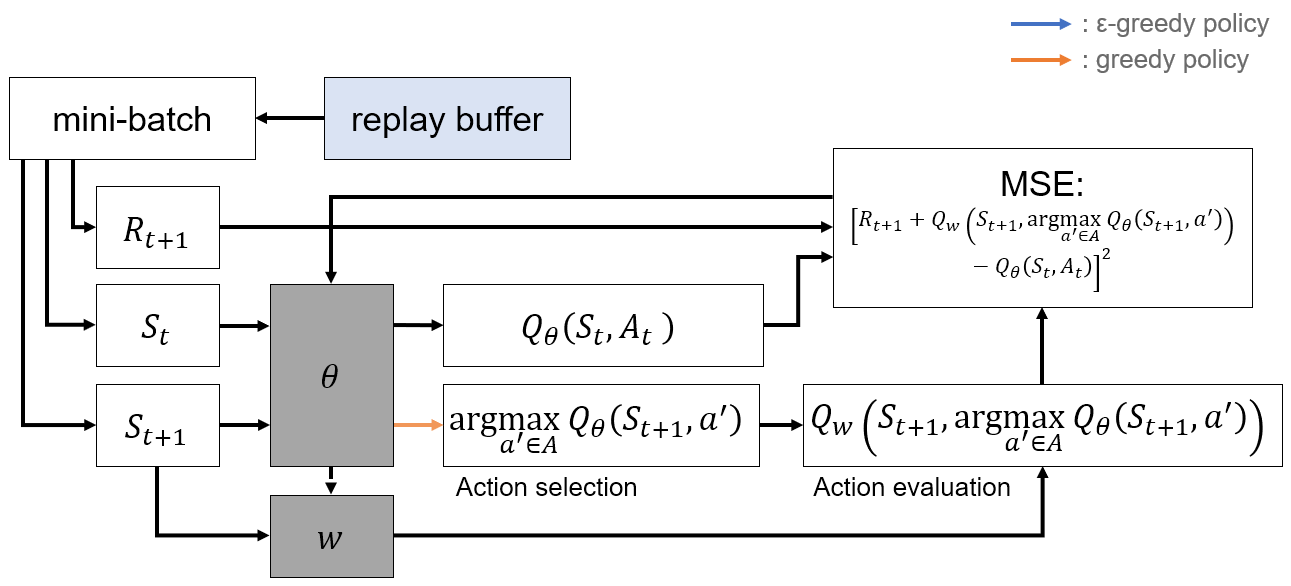
• 기존의 DQN의 update target은 $R_{t+1}+\gamma\max_{a'\in A}Q_w(S_{t+1},a')$
• 위 식을 다르게 표현하면, $R_{t+1}+\gamma Q_w(S_{t+1}, \argmax_{a' \in A}Q_w(S_{t+1},a'))$
• Action selection과 evaluation이 같은 network(Target network)에서 수행됨
• Greedy policy가 action selection에만 적용되지 않고 action evaluation에도 적용되어 "overestimation problem" 발생

Overestimation problem

• NN이 Q-value를 ground truth보다 더 높게 approximate하는 현상
• 모든 action에 대해 overestimation이 발생할 경우 큰 문제가 없을 수도 있음
• 그러나, 특정 action에 대해 overestimation이 발생할 경우 suboptimal policy로 수렴할 수 있음
• "Issues in using function approximation for reinforcement learning"(1993)에서 action space가 복잡해질 수록 overestimation이 악화됨을 증명

• DQN 기반의 algorithm
• DDQN은 overestimation problem을 해결하기 위해 action selection과 action evaluation을 분리
• Update target
  $R_{t+1}+\gamma Q_w(S_{t+1}, \argmax_{a' \in A}Q_\theta(S_{t+1},a'))$
  • Action selection: Policy network($\theta$)
  • Action evaluation: Target network($w$)
• DQN과 구조가 거의 동일하며, update target을 구하는 부분에만 차이가 존재

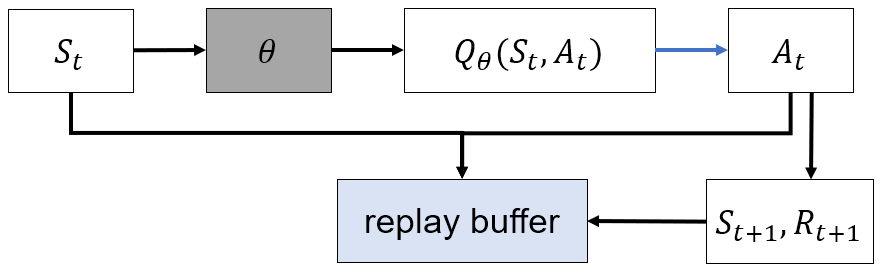
TD3(Twin Delayed Deep Deterministic Policy gradient)

• Value-based algorithm들에서 overestimation problem이 발생하는 것은 이미 알려져 있지만, policy-based algorithm들에서도 발생하는지는 밝혀지지 않음
• 본 논문에서는 policy-based algorithm들에서도 overestimation problem이 발생함을 밝혀냈고, 이를 해결하기 위한 algorithm인 TD3를 제안함

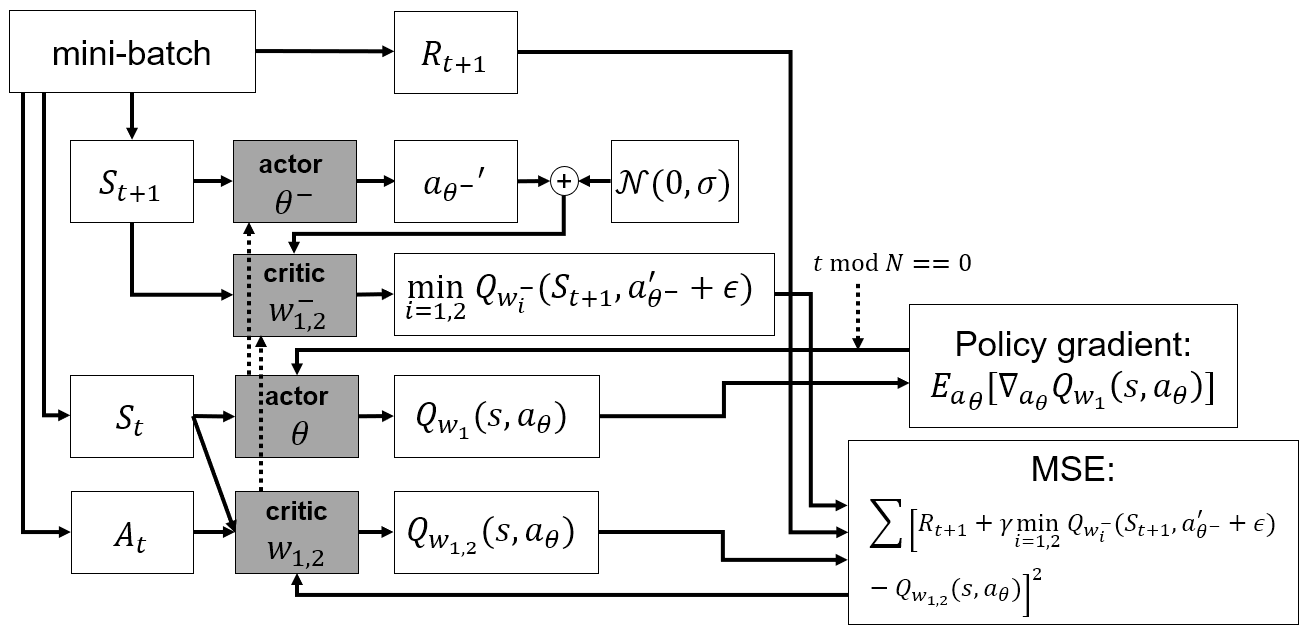
Clipped double Q-Learning

• Value-based algorithm들에서 overestimation problem을 해결하기 위해 적용했던 기법들이 policy-based algorithm들에서는 그다지 효과적이지 못하였음
• Critic network(value estimator)를 2개 사용
• Update target of Critic network
  $R_{t+1}+\gamma\min_{i=1,2}Q_{w_i^-}(S_{t+1},a_{\theta^-}')$
• 2개의 Critic network 중 작은 값을 사용함으로써 underestimate bias를 발생시킴
• Bias의 upper bound를 제한하므로써 overestimate problem을 완화할 수 있음

Delayed policy update

• Divergence problem
  • Actor은 policy gradient를 이용하여 network를 update하는데, policy gradient내에 Q-value가 포함되어 있음
    $c.f. \nabla_\theta J(\theta)\approx E_{a_\theta}[\nabla_{a_\theta}Q_w(S_t,a_\theta)]$
  • Q-value가 overestimate된 값이라면, 부정확한 Q-value로 인해 policy도 부정확해지는 문제가 존재
• Q-value error가 충분히 작아질 때 까지 Actor network의 update를 잠시 멈춤
• Critic network는 매 time step마다 update를 수행하며, Actor network는 $N$ time step마다 update를 수행

Target policy smoothing

• Overfitting problem
  • Deteministic policy는 replay buffer내의 sample로 부터만 학습이 가능
  • 따라서 Network가 sample들에 overfitting될 수 있음
• Regularization을 수행해주기 위해 action에 clipped gaussian noise를 추가해줌
  $R_{t+1}+\gamma \min_{i=1,2}Q_{w_i^-}(S_{t+1},a_{\theta^-}'+\epsilon)$
  $\epsilon=clip(\mathscr N(0,\sigma),-c,c)$

D4PG(Distributed Distributional Deep Deep Deterministic Policy Gradient)

Distributional critic update

Real world에서는 동일한 $S_t, A_t$에 대해서도 다른 reward $R_{t+1}$을 받을 수 있다. Distributional RL은 이러한 reward의 uncertainty를 학습한다.

Conventional RL은 Q-value를 scalar로 표현하며, 그에 따른 Bellman equation은 다음과 같이 표현된다.

Distributional RL은 Q-value를 distribution으로 표현하며, 그에 따른 distributional Bellman equation은 다음과 같이 표현된다.

Distributional RL은 reward의 uncertainty를 같이 학습하므로 좀 더 stable한 learning이 가능하다.

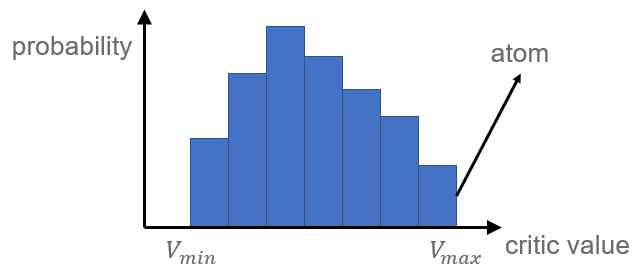
Q-value의 distribution은 value distribution이라 한다. Value distribution은 discrete distribution이며 action의 critic value가 가질 수 있는 범위를 $N$개로 나누어 각 범위에 대한 probability로 표현된다. 이 때 각 critic value 범위를 atom이라 한다. Atom의 갯수와 critic value의 최대/최소값$(V_{max},V_{min})$은 hyperparameter이다.

Target distribution은 distributional Bellman equation에 따라 $R_{t+1}+\gamma Z(S_{t+1},A_{t+1})$으로 표현되고, 이 값을 $[V_{min},V_{max}]$ 범위로 clipping한다.

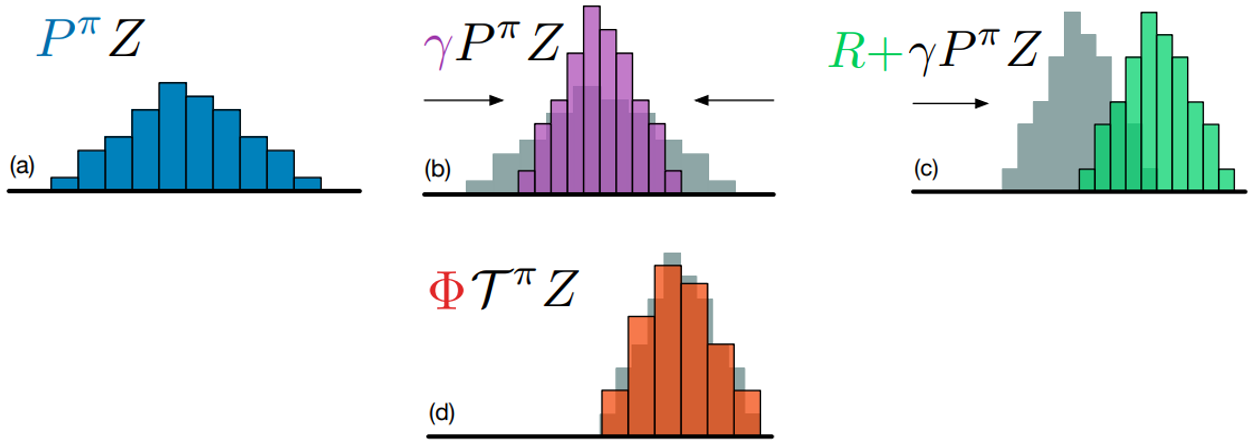
그러나 위의 그림과 같이 distributional Bellman equation을 적용하면 scaling과 shifting이 적용되어 target distribution의 atom이 갖는 값과 기존 distribution의 atom이 갖는 값이 달라지게 된다. 따라서, 이 둘의 atom 값을 맞추어 주기 위해 target distribution에 projection을 적용한다. 이후에는 기존 distribution이 target distribution과 유사해지도록 학습을 진행한다.

Distributed parallel actors

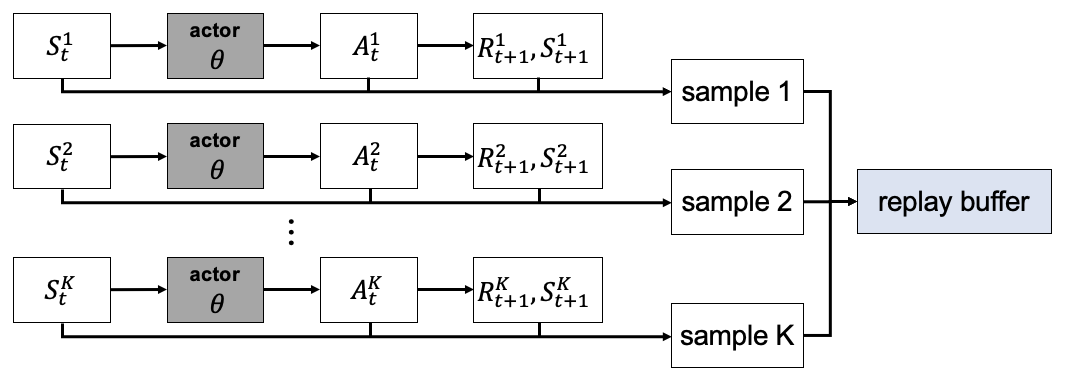
D4PG는 다수의 독립적인 actor들이 environment와 상호작용을 하며 sample을 수집한다. 이때 모든 actor들은 같은 weight를 공유하며, 일정 주기마다 새로운 weight로 update된다.

N-step returns

TD-error를 계산할 때 미래에 받을 reward도 고려하기 위하여 N-step returns을 사용한다.

N-step returns를 사용하는 경우 N개의 sample$(S_{t:N},A_{t:N},R_{t+1:t+N},S_{t+1:t+N})$로 부터 $R_D=\sum_{n=0}^{N-1} (\gamma^N R_{t+n+1})$을 계산한다. 이후 N개의 sample을 N-step returns를 사용하여 하나의 sample$(S_t,A_t,R_D,S_{t+N},\gamma^N)$으로 표현한다. 이 sample로 부터 구할 수 있는 target은 $Y_t=R_D+\gamma^N Z(S_{t+N},A_{t+N})$으로 표현된다.

PER(Prioritization of Experience Replay)

DQN, DDPG 등의 algorithm은 replay memory로 부터 sample들은 uniform하게 sampling하였다. 그러나 sample들 중에서 유의미한 sample의 갯수는 그리 많지 않으므로 uniform sampling은 비효율적이다. PER은 TD-error$(\delta)$를 이용하여 각 sample이 얼마나 'surprising'한지 평가하며, 의미가 있다고 평가된 sample을 좀더 비중있게 sampling한다.

각 sample은 priority$(p_i)$를 가지며 priority에 따른 sampling probability는 다음과 같이 표현된다.

Hyperparameter $\alpha$는 prioritization을 얼마나 적용할지 결정하며, $\alpha=0$ 인 경우 uniform sampling과 같아진다.

각 sample의 priority를 결정하는 방법은 크게 2가지 존재한다.

Proportional prioritization

Proportional prioritization은 TD-error $(\delta)$의 크기에 비례하여 priority를 설정하며, 다음과 같이 표현된다.

여기서 $\epsilon$은 굉장히 작은 상수이며, TD-error가 0인 sample이 zero-probability를 갖지 않도록 priority를 보정해주는 역할을 한다.

Rank-based prioritization

Rank-based prioritization은 단순히 TD-error를 내림차순으로 정렬하여 rank를 기반으로 priority를 설정한다.

PER을 사용하면 sampling에 bias가 발생하므로, importance-sampling(IS) weight를 통해 bias를 수정해준다.

위 식에서 $N$은 replay memory의 크기이다. Hyperparameter $\beta$는 compensation을 얼마나 적용할지 결정하며, $\beta=1$인 경우 최대의 compensation이 적용된다. 일반적으로 $\beta$는 $\beta_0>1$ 로 부터 $1$까지 linear하게 감소시킨다.

Distributional Bellman equation을 계산할 때 TD-error $\delta_i$ 대신 TD-error에 IS weight $w_i$를 곱한 $\delta_i \cdot w_i$ 를 사용하며, IS weight $w_i$는 안정된 학습을 위해 TD-error가 기존값보다 커지지 않도록 IS-weight의 최댓값이 1이 되도록 normalize 시켜준다.

PER은 time complexity를 줄이기 위해 일반적으로 segment tree형태로 구현되며 1개의 sum tree와 1개의 min tree로 구성된다. Sum tree는 sampling probability$\left( P(i)={p_i^{\alpha} \over \sum_k p_k^{\alpha}}\right)$ 에서 분모를 빠르게 계산하기 위해 존재한다. Min tree는 IS weight를 normalize하기 위해 존재한다. IS weight는 $w_i=\left( N \cdot P(i)\right)^{-\beta}$ 이며, $(N \cdot P(i)) > 0, \beta \geq 1$ 이므로 IS weight는 $P(i)$가 최소일 때 최댓값을 갖는다. $P(i)$은 $p_i$에 비례하므로, $p_i$가 최소일 때 IS weight가 최대가 되므로, $p_i$ 최솟값을 빠르게 구하기 위해 min tree가 존재한다.

Architecture

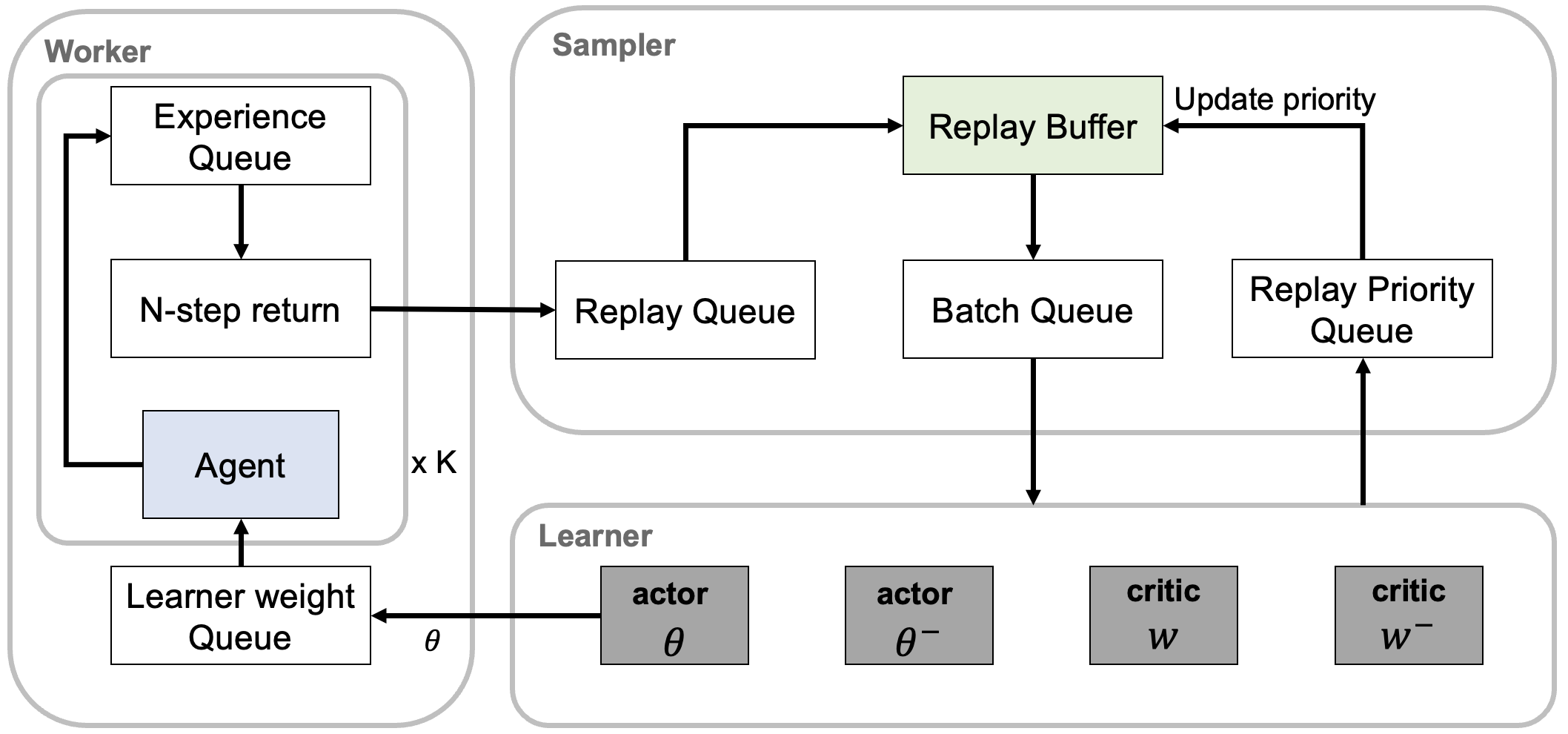
D4PG는 기능에 따라 worker, sampler, learner로 나누어 나타낼 수 있다.

Worker

다수의 독립적인 actor(agent)들이 environment와 상호작용을 하며 sample을 수집하며, 수집한 sample을 experience queue에 저장한다. Experience queue에서 N개의 sample을 사용해 N-step return을 계산한 후, N개의 sample을 1개의 sample로 재표현하여 replay queue에 저장한다. 모든 agent는 같은 weight$(\theta)$를 가지며, 일정 주기마다 learner weight queue로부터 새로운 weight를 가져와 사용한다.

Sampler

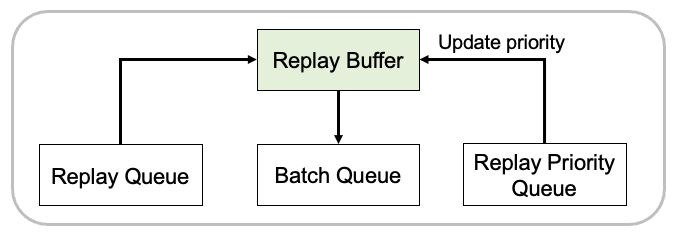
Replay queue의 sample들을 모아 replay buffer에 저장한다. 이후 replay priority queue에서 index와 IS weight를 가져와 replay buffer에 대해 priority를 update한다. 마지막으로 replay buffer에서 batch를 sampling하여 batch queue에 저장한다.

Learner

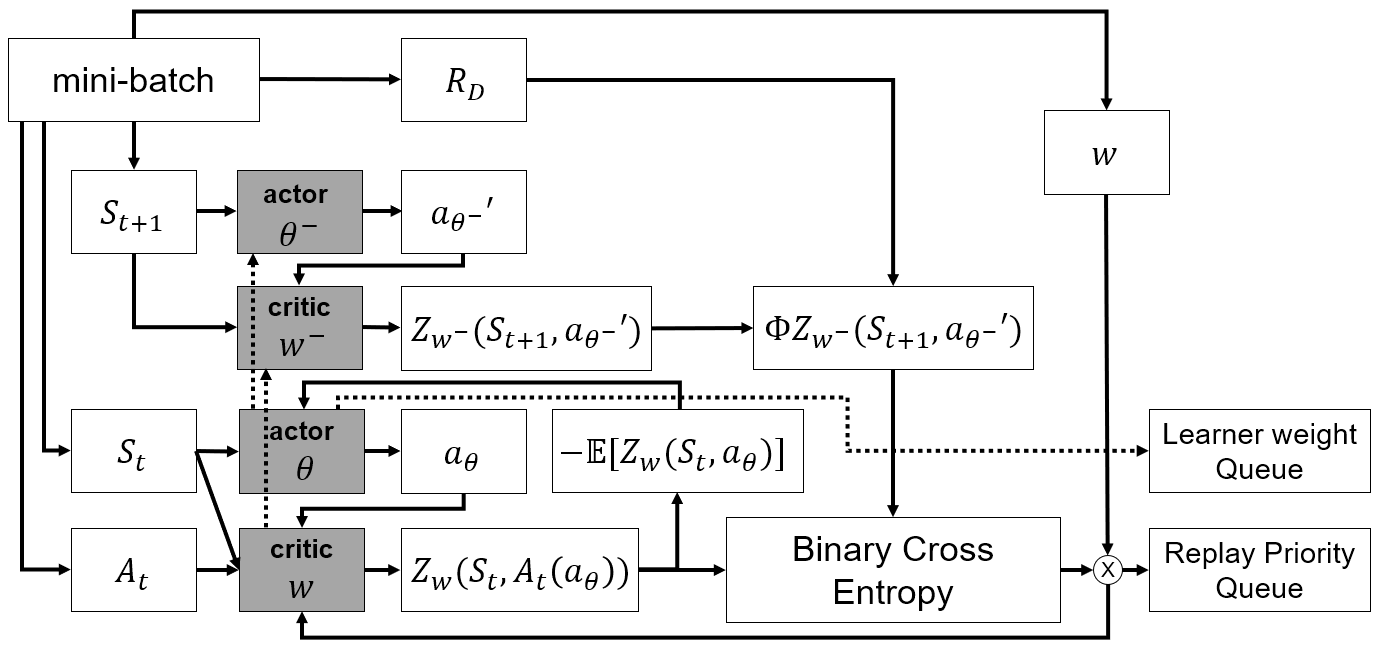
Batch queue로 부터 batch를 가져와 actor, critic network 학습을 수행한다. 일정 time step마다 actor의 weight를 learner weight queue에 저장하여 agent(actor)들이 사용하도록 하며, critic update에 사용된 TD-error를 replay priority queue에 저장하여 replay buffer의 priority update에 사용하도록 한다.

Algorithm

1. $S_t \rightarrow \theta^- \rightarrow a_{\theta^-}'$
2. $(S_{t+1}, a_{\theta^-}') \rightarrow w^- \rightarrow Z_{w^-} \rightarrow$ L2 projection $\rightarrow \Phi Z_{w^-}$
3. $(S_t, A_t) \rightarrow w \rightarrow Z_w$
4. critic loss: BCELoss($\Phi Z_{w^-}, Z_w)$
5. Update PER
6. optimize critic
7. $S_t \rightarrow \theta \rightarrow a_\theta$
8. $(S_t, a_\theta) \rightarrow w \rightarrow Z_w$
9. actor loss: $-E[Z_w]$ (atom $\times$ prob)
10. optimize actor
11. soft update $\theta^-, w^-$

Summary