A 65-nm 8-to-3-b 1.0–0.36-V 9.1–1.1-TOPS/W Hybrid-Digital-Mixed-Signal Computing Platform for Accelerating Swarm Robotics

JuYoung Oh·2022년 5월 18일

JSSC 2020

Problem to solve

Swarm algorithm은 learning-based method와 physical-model-based approach를 모두 사용한다.
Swarm robot의 processor는 micro controller, motor와 sensor에 비해 많은 energy를 소비한다.
Mixed-signal system은 low-bit에서는 energy efficient하지만, swarm size가 커짐에 따라 bit-width가 증가하면 digital system이 더 efficient하다.

How to solve

Hybrid-Digital-Mixed-Signal solution(HDMS)을 사용하여 scalability 채용.
3-5b 연산을 수행하는 Time-Domain Mixed-Signal(TDMS) kernel 사용.

Swarm algorithms

Physical model based algorithms

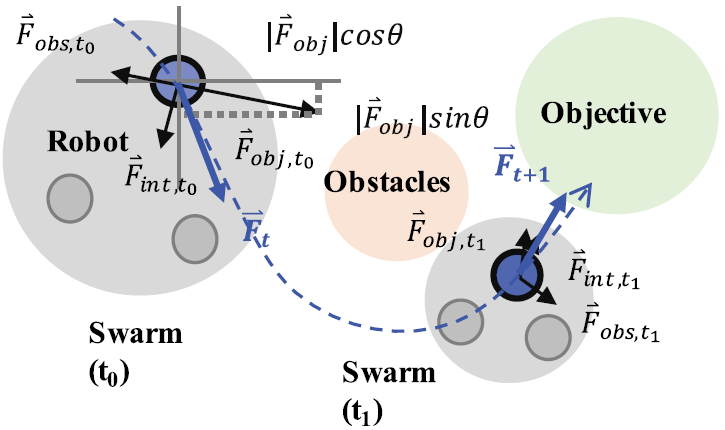
Physical model based algorithms 중에서 articifical potential field(APF) algorithm이 가장 널리 사용된다. APF는 robot과 주변 물체들이 electric field와 같은 가상의 potential field를 생성한다고 가정하여, potential field로 부터 motion vector를 계산한다. APF는 아래와 같은 식으로 표현된다.

m_i \frac{d \overrightarrow v_i}{dt}=\overrightarrow F_{pro,i}+\overrightarrow F_{int,i}+\overrightarrow F_{esp,i}+\overrightarrow F_{est,i}

$\overrightarrow F_{pro,i}$ 는 propulsion vector, $\overrightarrow F_{esp,i}$ 는 objective escape vector, $\overrightarrow F_{est,i}$ 는 stochastic force vector를 나타낸다.

각 potential function을 적절히 설정함으로서 control algorithm을 구할 수 있다.

Learning based Algorithms

Pre-defined model이 존재하지 않거나 완전하지 않은 경우, learning based algorithm을 주로 사용하며, RL-based cooperative Q-learning이 좋은 성능을 보여준다.

Single-agent Q-learning은 다음과 같은 식으로 표현된다.

Q_{t+1}(S_t,A_t)=Q_t(S_t,A_t)+\alpha(R_t+\gamma\max Q_t(S_{t+1},A_t)-Q_t(S_t,A_t))

Cooperative Q-learning은 local state와 local reward 대신 global state와 reward를 사용한다.

Cooperative Q-learning은 다음과 같은 식으로 표현된다.

Q_{t+1}(S_{t,global},A_t)=Q_t(S_{t,global},A_t)+\alpha(R_{t,global}+\gamma\max Q_t(S_{t+1,global},A_t)-Q_t(S_{t,global},A_t))

S_{t,global}=[S_{t,1}, S_{t,2},...,S_{t,N}]

Q-learning은 모든 state에 대한 Q-value를 Q-table 형식으로 저장한다. 그러나, environment가 복잡해지고, swarm size가 커질 수록 Q-table의 크기도 기하급수적으로 커지기 때문에 memory-constrained design에서는 Q-table을 사용하기 어렵다. 따라서, Q-value는 neural network의 output으로 근사시켜 사용한다.

Common computing platform

LPU(Linear Processing Unit)

Physical model based algorithm과 learning based algorithm 모두 vector와 matrix 연산이 주가 된다. 따라서, linear-processing이 두 연산 모두에서 가장 중요하다.

APF에서는 motion vector를 구하기 위해 linear operation이 필요하며, neural network에서는 linear 연산을 통해 Q-value를 구한다.

Non-Linear Processing Unit

두 algorithm 모두 linear 연산 뿐만 아니라 non-linear 연산도 수행된다.

APF에서는 각 potential function을 구할 때, $\sin, \cos, \tanh$ 등의 연산이 필요하며, non-linear operation이 수행된 다음에 linear operation이 수행된다.

Neural network에서는 linear operation이 수행된 다음에 non-linear한 activation function이 적용된다.

Non-linear processing unit은 LUT 기반으로 non-linear function을 piecewise approximation하여 연산을 수행한다.

Hybrid-Digital-Mixed-Signal Computing

Time domain에서 연산을 수행할 경우, digital system에 비해 throughput이 낮다. 그러나, robotics control 분야에서 요구되는 data processing speed는 그리 높지 않으므로 throughput을 약간 희생하고 energy efficency를 높일 수 있는 mixed-signal computing이 좋은 대안이다.

Mixed-signal computing은 5~6b 이하의 low-bit precision에서 좋은 energy efficieny를 보인다. 그러나, swarm size가 증가함에 따라 요구되는 bit precision은 증가하며, high-bit precision에서는 mixed-signal computing에 비해 digital system의 energy efficieny가 좋아지는 현상이 나타난다.

따라서, swarm size에 따라 mixed-signal computation과 digital computation을 같이 사용해야 energy efficiency를 높일 수 있다.

Time-Domain Multiplication and Accumulation

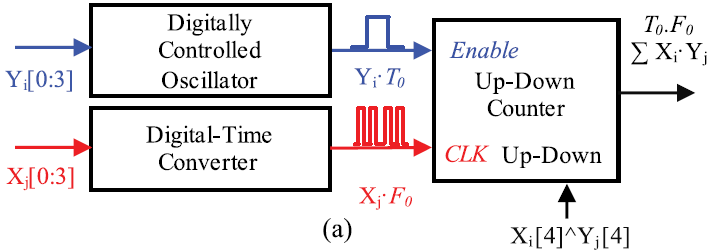
Time-based circuit은 5b data 간의 MAC 연산을 수행한다. 두 데이터의 MSB는 sign bit 이므로, 하위 4b 만을 연산에 사용한다. X는 DTC에 의해 크기에 비례하는 갯수를 가지는 pulse로 변환되며, Y는 DCO에 의해 크기에 비례하는 폭을 가지는 pulse로 변환된다. Pulse X는 counter의 clk 역할을 하며, Pulse Y는 counter의 enable 역할을 한다. X, Y의 MSB는 XOR 연산을 통해 counter의 방향(Up/Down)을 결정한다. Counter의 값을 통해 X, Y 간의 MAC 연산을 수행한다.

Hybrid-Digital-Mixed-Signal-Computing Platform

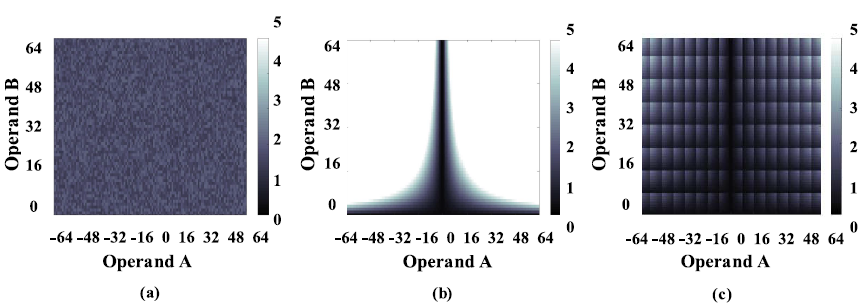
(a) digital (b) TDMS (c) HDMS

위의 그림은 operand의 bit precision에 따른 MAC 연산에 필요한 energy를 나타낸다.

Bit precision이 낮을 경우 time domain mixed signal의 경우가 digital에 비해 energy consumption이 낮지만, bit precision이 증가함에 따라 energy consumption이 빠르게 증가함을 확인할 수 있다. 이는 N-bit precision일 경우, time-based circuit의 switching 횟수가 $2^N$ 으로 증가하기 때문이다.

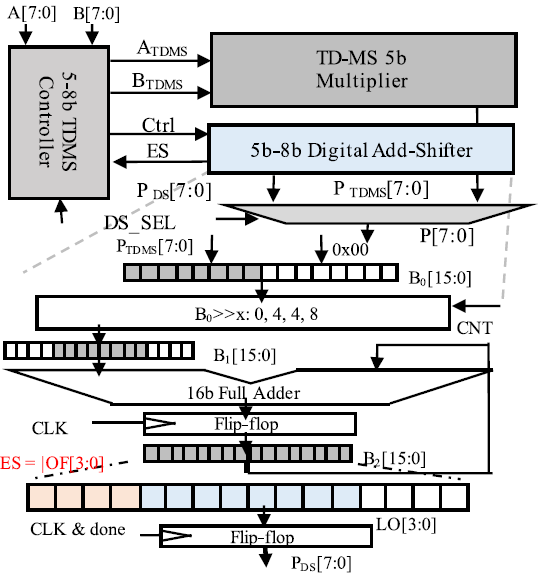
Hybrid-Digital-Mixed-Signal(HDMS)-Computing은 위와 같은 문제를 해결하기 위해 제안되었다. 5b TDMS를 사용하기 때문에, 5b 이하의 경우에는 TDMS 만을 사용한다. Shiter는 TDMS의 연산값을 0, 2, 4, 8b shift하여 16b adder를 통해 accumulate한다. 이를 통해 5b multiplier만으로 8b 까지의 multiplication을 수행할 수 있다.

HDMS는 TDMS에 비해 대략 4배 정도의 cycle을 필요로 하지만, TDMS는 bit precision이 높아짐에 따라 연산에 필요한 cycle이 $2^N$ 으로 증가하므로, TDMS에 비해 HDMS의 throughput이 높다. 그럼에도 불구하고 HDMS는 digital system에 비해서 throughput이 낮은데, robotics control의 경우 아주 높은 throughput이 요구되자 않으므로, HDMS의 throughput 정도면 충분하다고 저자는 주장한다.

Architecture

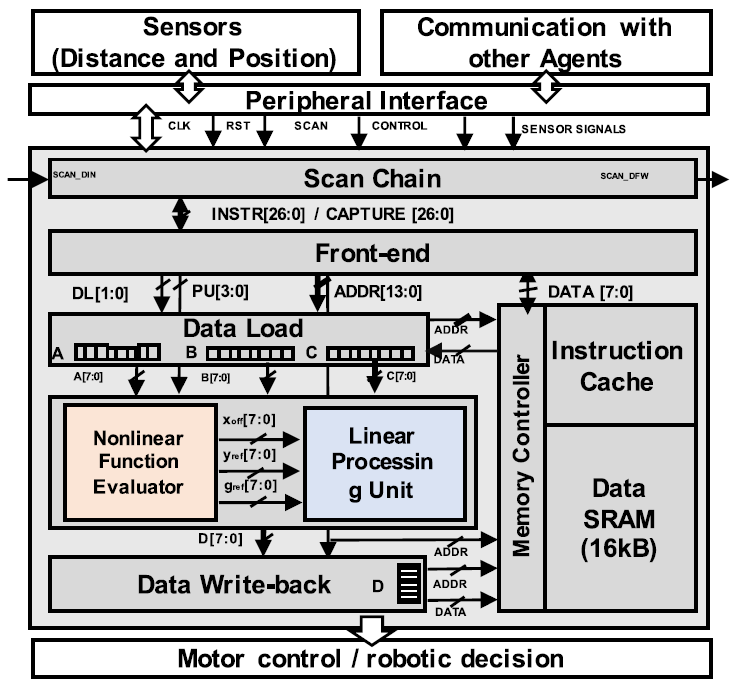
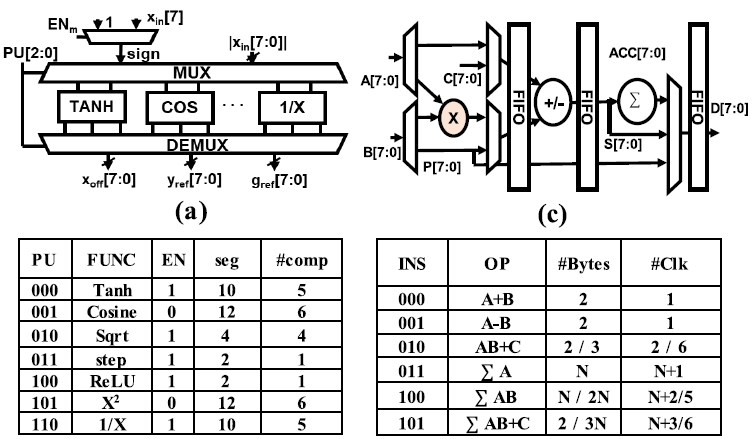
전체적인 architecture는 위의 그림과 같다.

NFE(Non-linear Function Evaluator)

NFE는 non-linear function들을 piecewise linear approximate하여 나타낸다. Function과 input을 NFE에 입력하면, NFE는 offset( $x_{off}$ ), reference gradient( $g_{ref}$ ), reference offset( $y_{ref}$ )를 생성한다. 이 값은 LPU에서 연산되어 결과값을 만들어낸다.