이분탐색 (Binary Search)과 파라매트릭 서치(Parametric Search)

이분탐색 (Binary Search)

Binary Search란?
탐색 범위를 절반씩 줄여 나가면서 원하는 데이터 찾는 방식

🕐TIME COMPLEXITY : O(logN)

** 중요 포인트 : 정렬되어 있어야 한다!!

이분탐색 진행 방식

• 중간값 mid를 찾아서 원하는것보다 크다면(작다면) end(start)값에 mid값을 넣어서 범위를 줄여간다

start, end에 mid/mid+1/mid-1을 넣는지 어떻게 알죠???
--> 문제에 따라 다르게 설정해야 한다고 생각합니다.
예를 들어 정확한 데이터를 찾는것이 아닌 가능한 최소/최대값을 찾는 문제면 원하는 답이 나왔어도 최소/최대인지 모르기 때문에 범위에 포함시켜서 계산해야 할 수도 있습니다.
하지만 정확한 특정 데이터를 찾는데는 문제가 없으니 편한대로 해도 될거 같습니다.

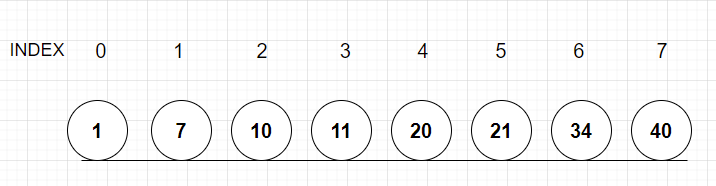
1. 처음 상황 (정렬되어 있어야 한다!!)
1,7,10,11,20,21,34,40 데이터에서 10을 찾으려고 한다

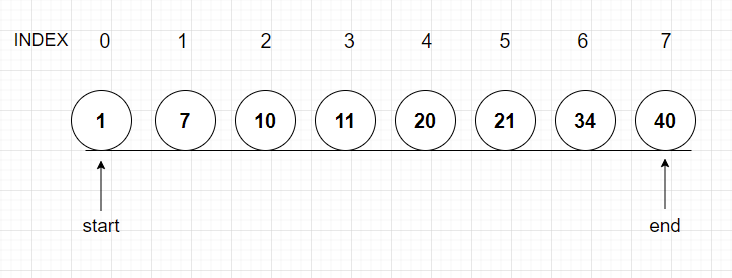
2. 가운데 값을 찾아 원하는 데이터와 크기 비교한다
인덱스 기준으로 (start+end)/2를 mid라고 생각한다
==> (0+7)/2 = 3.xx 이므로 3인덱스를 mid로 선택한다

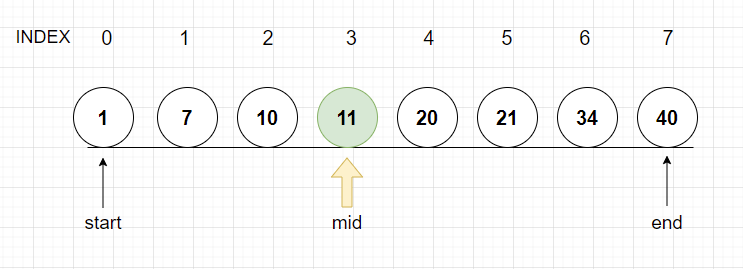
11은 원하는 10보다 크므로 end에 mid값을 넣는다

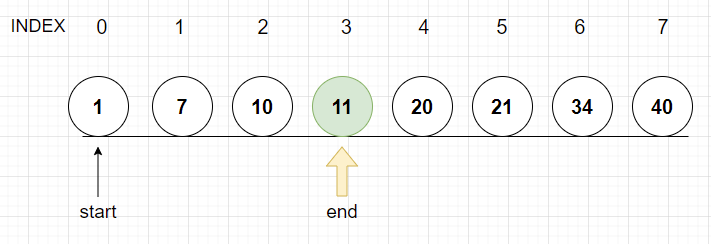
3. 2번과정을 반복한다
(start+end)/2 ==> (0+3)/2 = 1.xxx 이므로 1인덱스를 mid로 선택한다

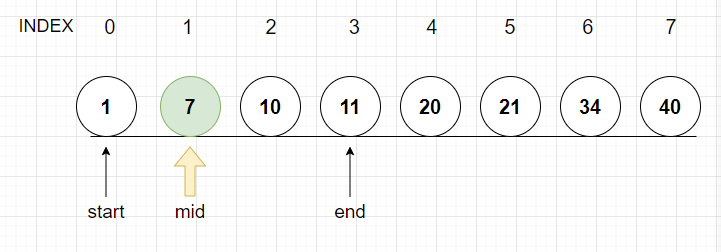
7은 원하는 10보다 작으므로 start에 mid값을 넣는다

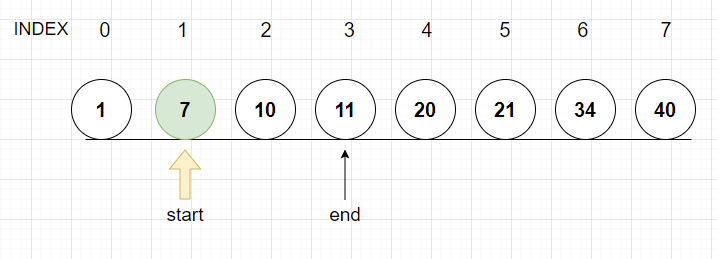
4. 한번더 반복한다
(start+end)/2 ==> (1+3)/2 = 2 이므로 2인덱스를 mid로 선택한다

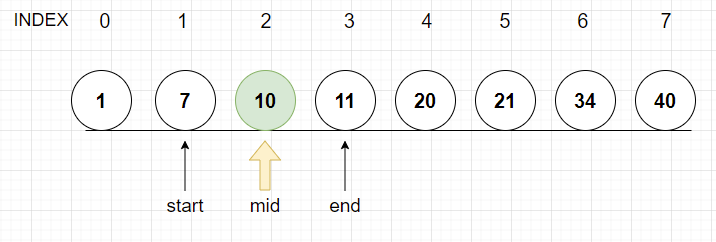
10은 원하는 데이터이므로 검색에 성공했다!

파라매트릭 서치(Parametric Search)

Parametric Search란?
최적화 문제를 결정문제로 바꾸어 푸는 것이다!

🕐TIME COMPLEXITY : O(logN)

** 이분탐색과 다른 점 : 결정문제인지 아닌지의 차이!

이게 무슨말인가하면...
가능한 답 중 최소/최소를 찾아라! ===> 이 답이 가능한가?!
최소/최대를 찾는 것보단 답이 가능/불가능이 더 쉽고 직관적이다.

이 또한 예시를 들어 진행방식을 설명하려고 한다.

---

---

---

풀이 문제

BOJ 3079 입국심사

문제 간단 설명 :
7,10초 걸리는 입국심사대 2개가 있다. 6명이 입국심사할때 걸리는 최소의 시간은??

파라매트릭 서치 진행 방식

1. 초기세팅 : start와 end를 설정한다

여기서 end를 42로 세팅한 이유?
=> 가능한 가장 긴 시간은 10x6=60초이지만 답이 될 수 있는 가장 긴 시간은 7x6=42초이기 때문에 조금이라도 범위를 좁히기 위해서 42초를 선택했다.

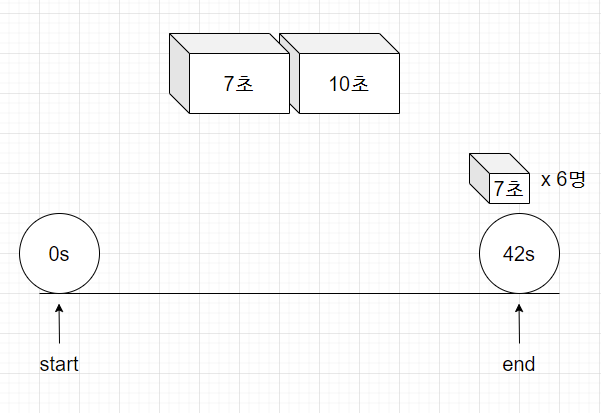
2. mid값을 구해 답으로 가능/불가능한지 확인한다
(start+end)/2 = (0+42)/2 = 21초
21초동안 3명(7초 심사대)과 2명(10초 심사대) 처리 가능 => 총5명 ==> 부족하다
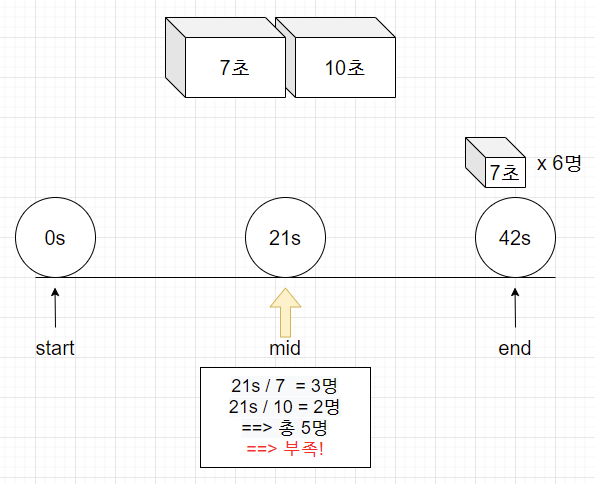
시간이 부족하기 때문에 21초보다 큰값이 있는 범위에서 처리해야 한다 => start를 22초로 변경!(21초는 어차피 답이 될 수 없으므로 범위에서 제외)


3. mid값을 구해 답으로 가능/불가능한지 확인한다
(start+end)/2 = (22+42)/2 = 32초
32초동안 4명(7초 심사대)과 3명(10초 심사대) 처리 가능 => 총7명 ==> 초과한다
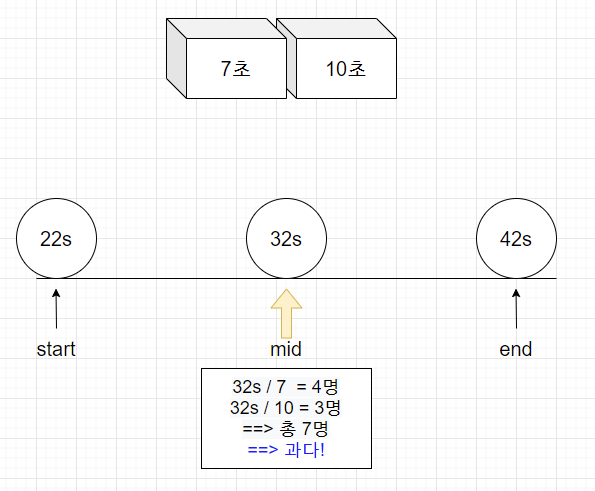
시간이 남기 때문에 32초보다 작은 값이 있는 범위에서 처리해야 한다 ==> end를 32초로 변경!


4. mid값을 구해 답으로 가능/불가능한지 확인한다
(start+end)/2 = (22+32)/2 = 27초
27초동안 3명(7초 심사대)과 2명(10초 심사대) 처리 가능 => 총5명 ==> 부족하다
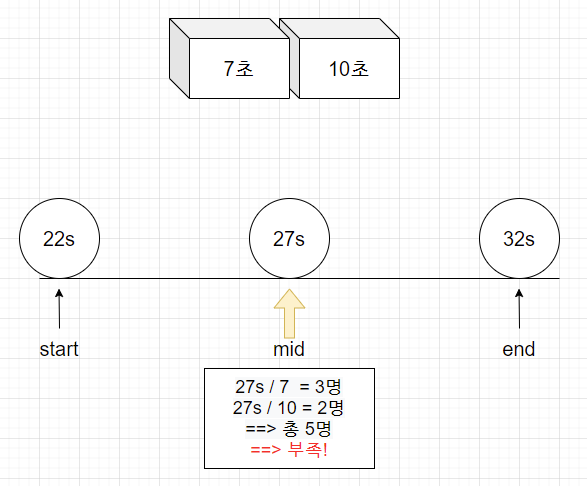
시간이 부족하기 때문에 27초보다 큰값이 있는 범위에서 처리해야 한다 => start를 28초로 변경!(27초는 어차피 답이 될 수 없으므로 범위에서 제외)


5. mid값을 구해 답으로 가능/불가능한지 확인한다
(start+end)/2 = (28+32)/2 = 30초
30초동안 4명(7초 심사대)과 2명(10초 심사대) 처리 가능 => 총7명 ==> 초과한다
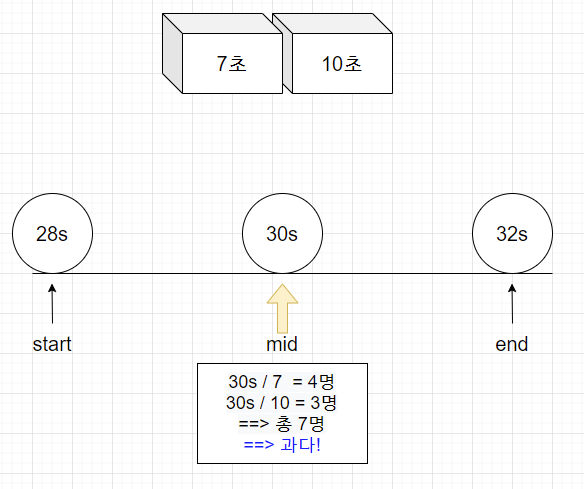
시간이 남기 때문에 30초보다 작은 값이 있는 범위에서 처리해야 한다 ==> end를 30초로 변경!


6. mid값을 구해 답으로 가능/불가능한지 확인한다
(start+end)/2 = (28+30)/2 = 29초
29초동안 4명(7초 심사대)과 2명(10초 심사대) 처리 가능 => 총6명 ==> 적정
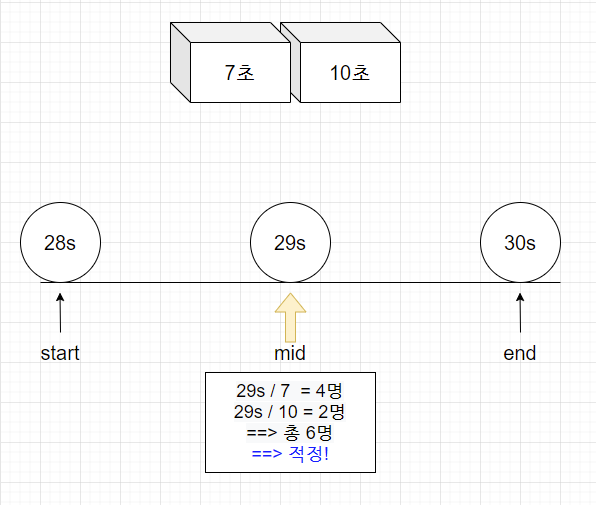
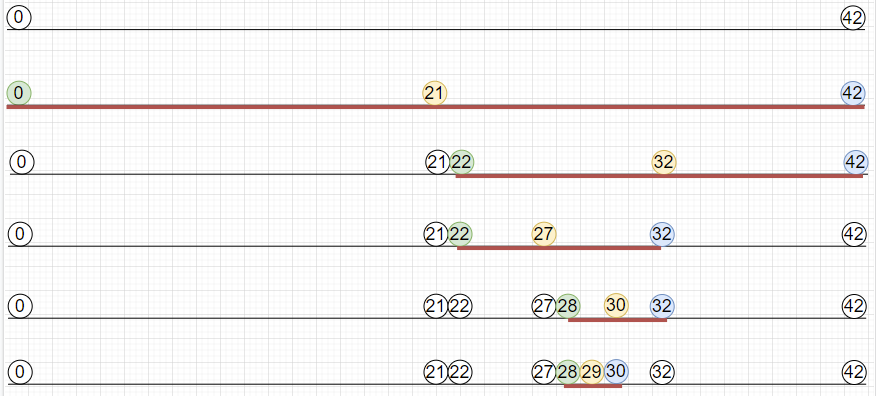답이 될수 있는 값이지만 더 작은 값이 존재할 수 있기 때문에 계속 진행한다 ==> end를 29초 변경!


7. mid값을 구해 답으로 가능/불가능한지 확인한다
(start+end)/2 = (28+29)/2 = 28초
28초동안 4명(7초 심사대)과 2명(10초 심사대) 처리 가능 => 총6명 ==> 적정
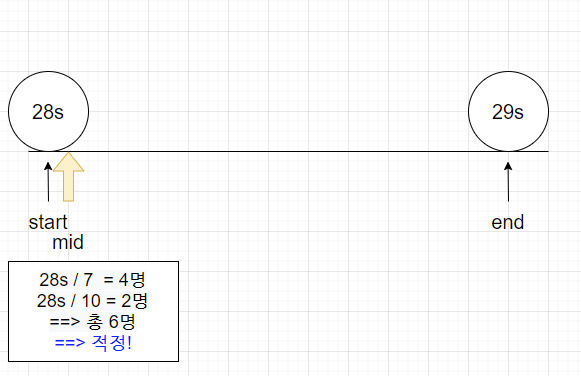
답이 될수 있는 값이지만 더 작은 값이 존재할 수 있기 때문에 계속 진행한다 ==> end를 28초 변경!


8. start와 end가 같은 값이 되므로 28초가 답이 된다

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main{

	private static int[] simsa;
	private static long M;
	private static int N;

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine(), " ");
		
		N = Integer.parseInt(st.nextToken());
		M = Integer.parseInt(st.nextToken());
		
		simsa = new int[N];
		
		for (int i = 0; i < N; i++) {
			simsa[i] = Integer.parseInt(br.readLine());
		}
		
		Arrays.sort(simsa);
		
		System.out.println(findAnswer(0,simsa[0] * M));
	}

	/**이분탐색 함수*/
	private static long findAnswer(long start, long end) {
		if(start>=end) return start; // 같거나 크면 리턴
		
		long mid = (start+end)/2; // 가운데 값
		long cnt = 0;
		
		for (int i : simsa) { // 가능한 횟수 체크하기
			cnt += mid/i;
		}
		
		if(cnt>=M)	return findAnswer(start, mid);
		else		return findAnswer(mid+1, end);

	}

}