Minimum Spanning Tree
간선들의 합이 최소인 Spanning Tree를 선택한다
신장트리(Spanning Tree) 란?
그래프 내 모든 정점을 포함하지만 사이클은 없는 트리
n개의 정점으로 이루어진 무향 그래프에서 n개의 정점과 (n-1)개의 간선으로 이루어진 트리
MST의 특징
- 간선의 합이 최소여야 한다
- n개의 정점을 다 포함하고, (n-1)개의 간선을 포함한다
- 사이클이 없다
EX. 주어진 그래프 모양
MST 그래프
MST를 만들려면 어떤 알고리즘을 사용해야 할까?
Prim 알고리즘(정점 선택)
하나의 정점에 연결된 간선 중 가장 최소비용인 것을 선택하면서 MST 생성
- 임의의 정점 하나 선택
- 선택된 정점들과 인접하는 정점들중 최소비용인 정점을 선택
- 모든 정점이 선택될 때까지 1,2방법 반복
- 서로소인 2개 집합을 유지한다
1) 처음 시작 정점을 선택한다(0번 정점)
0에서 제일 적은 비용인 31간선으로 2와 연결한다
2) 2번 정점 선택 ⇒ 선택처리 & 비용 업데이트
0,2번 정점에서 최소비용 간선 선택한다(이미 방문한 정점은 고려x)
제일 비용이 작은 21간선으로 1과 연결한다
3) 1번 정점 선택 ⇒ 선택처리 & 비용 업데이트
0,1,2 정점에서 최소비용 간선 선택한다 => 25 간선 연결된 6정점 선택
4) 6번 정점 선택 ⇒ 선택처리 & 비용 업데이트
0,1,2,6 정점에서 최소비용 간선 선택한다
=> 32 간선 선택x
=> 46 간선 연결된 4번선택
5) 4번 정점 선택 ⇒ 선택처리 & 비용 업데이트
0,1,2,4,6 정점에서 최소비용 간선 선택한다
=> 32 간선 선택x
=> 34 간선 연결된 3번선택
6) 3번 정점 선택 ⇒ 선택처리 & 비용 업데이트
0,1,2,3,4,6 정점에서 최소비용 간선 선택한다
=> 18 간선 연결된 5번 선택
7) 5번 정점 선택 ⇒ 선택처리 & 비용 업데이트
N개의 정점이 다 선택되었으므로 종료한다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class MST2_PrimTest {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[][] adjMatrix = new int[N][N];
boolean[] visited = new boolean[N];
int[] minEdge = new int[N];
StringTokenizer st = null;
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine(), " ");
for (int j = 0; j < N; j++) {
adjMatrix[i][j] = Integer.parseInt(st.nextToken());
}
minEdge[i] = Integer.MAX_VALUE;
}
int result = 0;
minEdge[0] = 0;
for (int c = 0; c < N; c++) {
int min = Integer.MAX_VALUE; // 최소 가중치 들어갈 변수
int minVertex = 0; // 정점번호
//신장트리에 연결되지 않은 정점 중 minEdge비용이 최소인 정점 결정하기
for (int i = 0; i < N; i++) {
if(!visited[i] && min > minEdge[i]) {
min = minEdge[i];
minVertex = i;
}
}
result += min; //정점 추가하면서 비용추가
visited[minVertex] = true; // 현재최소비용정점 방문처리
for (int i = 0; i < N; i++) {
// 방문한적 x && 간선이 연결되어 있음 && 비용이 더 작은 것이 있을때
if(!visited[i] && adjMatrix[minVertex][i] != 0 && minEdge[i] > adjMatrix[minVertex][i]) {
minEdge[i] = adjMatrix[minVertex][i];
}
}
System.out.println(result);
}
}
}Kruscal 알고리즘(간선 선택)
제일 작은 순으로 간선을 선택해서 MST 생성
- 모든 간선을 오름차순으로 정렬
- 가중치 낮은 간선부터 선택하면서 트리 증가
- 사이클 존재하면 다음 간선 선택
- N-1개의 간선선택될때까지 2번 반복
1) 비용 오름차순으로 간선을 정렬한다
각 정점은 크기가 1인 집합으로 만든다
2) 제일 비용이 작은 18 간선을 선택 => 3,5 정점 union 처리
편의상 root값은 숫자가 제일 작은 값으로 정한다
3) 제일 비용이 작은 21 간선을 선택 => 1,2 정점 union 처리
4) 제일 비용이 작은 25 간선을 선택 => 2,6 정점 union 처리
2는 이미 1과 같은 집합이므로 6이 1,2와 같은 집합에 들어간다
5) 제일 비용이 작은 31 간선을 선택 => 0,2 정점 union 처리
2는 이미 1,6과 같은 집합이므로 0이 1,2,6과 같은 집합에 들어간다
6) 제일 비용이 작은 32 간선을 선택 => 0,1 정점 union 처리
===> 이미 같은 집합이기 때문에 false
===> 그 다음 34 간선 선택 => 3,4 접점 union 처리
7) 제일 비용이 작은 40 간선을 선택 => 4,5 정점 union 처리
===> 이미 같은 집합이기 때문에 false
===> 그 다음 46 간선 선택 => 2,4 접점 union 처리
===> N-1 개의 간선 다 선택했으므로 종료
package com.ssafy.graph;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class MST1_KruskalTest {
static class Edge implements Comparable<Edge>{
int from,to,weight;
public Edge(int from, int to, int weigtht) {
super();
this.from = from;
this.to = to;
this.weight = weigtht;
}
@Override
public int compareTo(Edge o) {
// return this.weight - o.weight;
return Integer.compare(this.weight, o.weight);
}
}
static int V,E;
static int parents[];
static Edge[] edgeList;
static void make() { // 크기가 1인 단위집합을 만든다.
for (int i = 0; i < V; i++) {
parents[i] = i;
}
}
static int findSet(int a) {
if(parents[a]==a) return a;
// return findSet(parents[a]); //path compression 전
return parents[a] = findSet(parents[a]); //path compression 후
}
static boolean union(int a, int b) {
int aRoot = findSet(a);
int bRoot = findSet(b);
if(aRoot == bRoot) return false;
parents[bRoot] = aRoot;
return true;
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
parents = new int[V];
edgeList = new Edge[E];
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine(), " ");
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edgeList[i] = new Edge(from, to, weight);
}// 간선리스트
// 1. 간선리스트 가중치 기준 오름차순 정렬
Arrays.sort(edgeList);
make();
int result = 0;
int count = 0; // 선택한 간선 수
for (Edge edge : edgeList) {
if(union(edge.from, edge.to)) { // 싸이클이 발생x
result += edge.weight;
if(++count == V-1) break;
}
}
System.out.println(result);
}
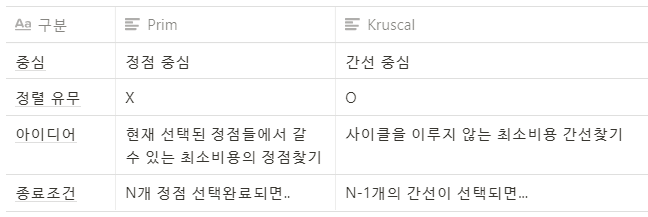
}Prim VS Kruscal
관련 문제
그 외 문제들
