1. 데이터의 압축

데이터의 압축 (data compression) 🔔

화일 정보를 더 작은 공간에 저장되도록 인코딩
저장공간의 절약 , 전송시간 단축

1. 다른 표기법의 사용 🔔

• 미국의 50개주 : 16비트 -> 6비트로 50개 주 표현가능
  -> 압축 ex) LA, NY , OK... etc

• 인코딩이나 디코딩 알고리즘이 매우 단순

• 문제점

  인코딩 부분을 사람이 읽을 수 없다
  인코딩 ,디코딩을 위한 시간이 소비된다
  주소화일을 처리하는 모든 S/W가 인코딩 , 디코딩 모듈 포함

2. 반복되는 열의 삭제: 진행-길이 인코딩 🔔

• 방법 : Triple로 표현 <ff , value , count >

• ex)

-> 24 ( 7번 ) , 26( 6번 ) 압축 18byte -> 11byte

• 희소 행렬 , 기기 데이터 , 텍스트를 포함하는 많은 종류의 데이터에 적용

• 특정한 양의 공간 절약을 보장하지 않음( -> 원래 데이터보다 더 커질 수도 있음 )

3. 가변 길이 코드의 대입 : Huffman code 💯

• 화일 내에서의 출현 빈도가 문자마다 다르다는 사실에 착안
• 데이터 집합에 나타나는 값의 확률을 결정
• 각 값에 대한 탐색 경로가 그 값에 대한 코드를 이진트리로 구성
• 빈도가 높은 문자에 적은 자리수 코드 부여

-> a는 0.4%확률 , b는 0.1% .....

✔ 코드 생성 예제

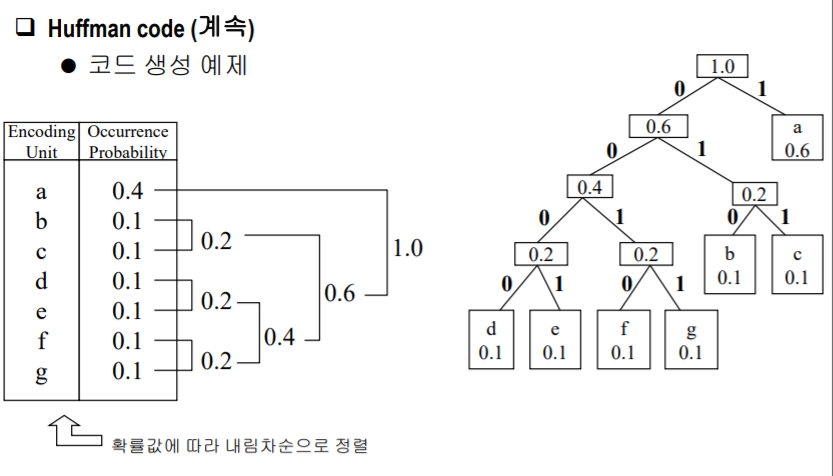
-> a : 0.4임 (표 오류)

-> 트리를 따라 가면 알파벳의 code 알수 있음

2. 파일의 재생 이용 공간

1. 레코드 삭제와 저장 공간의 축약

Mo만 사라지고 삭제되지 않았다. (*를 찾아서 Ames , Brown 레코드를 합친다 )

2. 동적인 공간 재사용을 위한 고정 길이 레코드의 삭제

1.고정 길이 레코드

삭제된 레코드 공간의 재사용 문제를 단순하게 처리가능

• 여유 공간을 순서적으로 재활용하는 레코드 삭제

삭제된 레코드가 차지한 공간을 알 수 있도록 하여 , 레코드를 삽입할 때 그 공간을
재사용할 수 있도록 함

• 레코드 삭제 기법

삭제되는 레코드에 특별한 표기 : *

• 삭제된 레코드에 대한 공간의 재사용

재사용 가능한 레코드 슬롯 RRN

3. 연결 리스트 및 스택

• 가용 리스트 : 화일 내에 사용 가능한 공간인 삭제 레코드를 연결 (리스트의 끝 : -1 사용)

• 모든 노드의 삽입과 삭제가 리스트 한 쪽 끝에서 발생하는 리스트

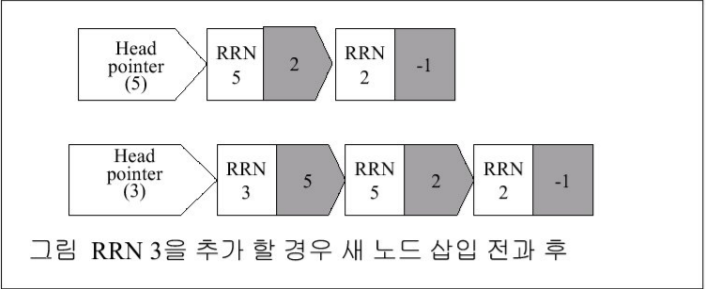
-> 삭제 된 것 끼리 연결 시킴 ( -1 이면 뒤에 삭제 된 것 없다는 뜻)

-> List head 에 가장 최근 삭제된 것을 저장

-> new record (새로운 레코드)를 저장하려고 하면 최근 삭제된 레코드에 저장하고
List head 에는 저장한 부분과 연결되어 있던 레코드를 넣어줌

1과 5가 연결 되어있으므로 new 1 레코드는 1번에 저장되고 , List head에는 5가 저장된다.

2. 가변길이 레코드의 삭제

• 가변길이 레코드의 가용 리스트

VariableLengthBuffer : 레코드의 시작 부분에 각 레코드의 길이를 정의
가용 리스트 : 링크는 바이트 오프셋을 포함

• 저장공간 단편화(가변길이 레코드)

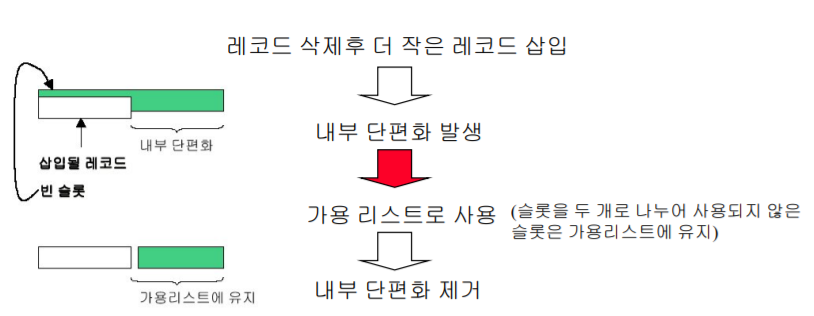
4. 배치 전략

• 최초적합 배치기법

  가용 리스트는 삭제된 레코드를 앞에 삽입
  충분히 큰 레코드 슬롯을 찾을 때까지 처음부터 레코드 탐색

• 최적적합 배치기법

  가용리스트를 크기에 따라 오름차순에 따라 순서화
  삽입할 레코드를 포함할 정도로 큰 것 중 제일 작은 슬롯을 사용
  단점: 외부 단편화, 추가 처리 시간

• 최악적합 배치기법

  가용리스트를 크기에 따라 내림차순으로 정리
  항상 가장 큰 레코드 슬롯을 반환
  장점 : 가용리스트의 첫 번째 요소만을 찾도록 단순화, 외부단편화 가능성 줄임

3. 빠른 검색

• 보조 기억장치에 대한 접근 비용이 매우 크기 때문에, 이를 최소화 할 수 있는 정렬 및
  검색 방법이 필요

(1) 단순 필드와 레코드 화일에서의 조회

RRN이나 byte offset을 알지 못할 때, 현재까지 키를 사용한 접근은 순차 탐색을 의미함

(2) 추측에 의한 검색: 이진탐색

1000개의 고정길이 레코드를 가지고 있고 키를 사용하여 오름차순으로 정렬된 파일
Jane Kelly 라는 레코드를 이진 탐색으로 찾는 방법 : 최대 10번 비교

이진 탐색 알고리즘

(3) 이진 탐색 대 순차 탐색

• 이진 탐색(n개의 레코드)

  최대 log2n +1 번 비교
  O(log2n)의 복잡도

• 순차 탐색일 경우 : 최대 n번 비교 , 평균 n/2번 비교

  O(n) 의 복잡도
  2000 개의 레코드로 이루어진 화일에서 Jane Kelly 레코드 찾기
  -이진 탐색 : 최대 1+log2(2000) = 11 비교
  -순차 탐색 : 평균 1/2*n = 1000 비교

• 이진 탐색에서 고려해야 할 비용

  키에 대해서 정렬되어 있어야 가능

• 정렬은 화일 처리에서 매우 중요

(4) 메모릴에서의 디스크 화일 정렬

• 내부 정렬 : 디스크에서 메모리로 전체 화일을 읽어 메모리 내에서 정렬

  탐색과 디스크 내에서의 많은 이동에 대한 비용을 줄임
  메모리 공간이 충분할 때 가능한 해결책

(5) 이진 탐색과 내부 정렬의 제약

• 문제점1 : 이진 탐색은 다수의 디스크 접근을 필요로 한다.

  키에 의한 반복된 접근이 많다면 탐색을 위한 비용이 큼 (예, 1000 개의
  레코드 : 9.5회의 접근)

• 문제점 2 : 화일을 정렬하여 유지하는 것은 매우 비싸다

  레코드 삽입시 : 평균적으로 레코드들의 절반 Read, 기존 레코드의 이
  동 요구

• 문제점3 : 내부 정렬은 단지 작은 화일에서만 적용

  화일이 너무 클 경우 : 외부 정렬 방법을 이용
  키 정렬(key sort) : 내부 정렬의 응용