Probability
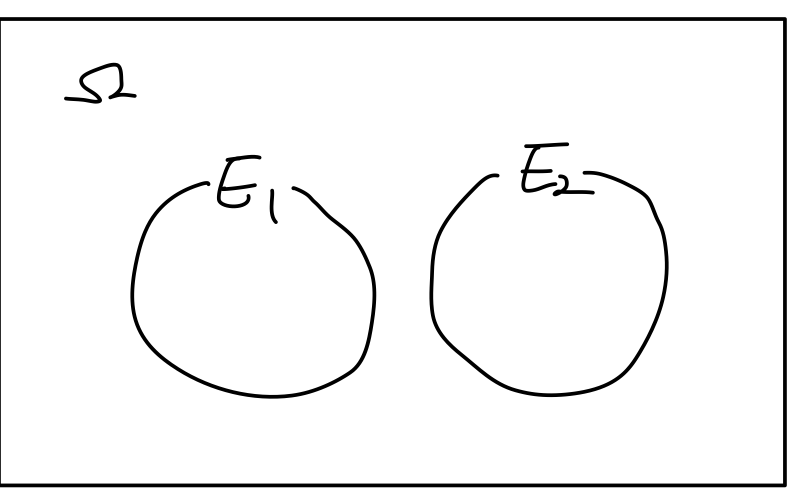
Event E1과 E2가 있다고 하자. 모든 사건을 Ω \Omega Ω
P ( E ) ∈ R ( c o n t i n u o u s v a l u e ) , P ( E ) ≥ 0 , P ( Ω ) = 1 P(E)\in R (continuous\ value),\ P(E)\ge0,\ P(\Omega)=1 P ( E ) ∈ R ( c o n t i n u o u s v a l u e ) , P ( E ) ≥ 0 , P ( Ω ) = 1
Subsequent characteristicsA ⊆ B t h e n P ( A ) ⊆ P ( B ) , P ( ∅ ) = 0 , 0 ≤ P ( E ) ≤ 1 P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B ) , P ( E c ) = 1 − P ( E ) A\subseteq B\ then\ P(A) \subseteq P(B),\\ P(\varnothing)=0,\quad 0\le P(E) \le1\\ P(A \cup B)=P(A)+P(B)-P(A \cap B),\quad P(E^c)=1-P(E) A ⊆ B t h e n P ( A ) ⊆ P ( B ) , P ( ∅ ) = 0 , 0 ≤ P ( E ) ≤ 1 P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B ) , P ( E c ) = 1 − P ( E )
Conditional Probability
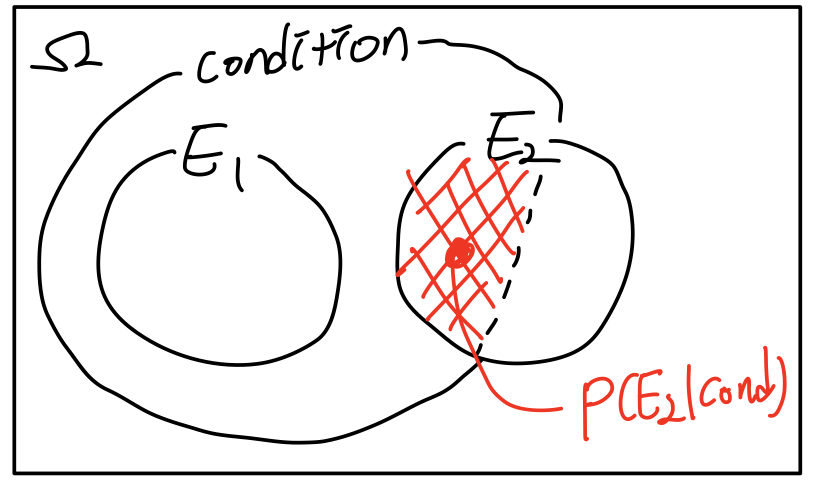
조건부확률은 위의 Probability에서 다루고자 하는 Scope=condition을 주어 다루는 것을 말한다.
즉, B가 참일 때 A일 확률은
P ( A ∣ B ) = P ( A ∩ B ) P ( B ) P(A|B)=\frac{P(A \cap B)}{P(B)} P ( A ∣ B ) = P ( B ) P ( A ∩ B ) 으로 표현할 수 있다. 이것을 다르게 표현하면 아래와 같다.
P ( B ∣ A ) = P ( B ∩ A ) P ( A ) → P ( B ∩ A ) = P ( B ∣ A ) P ( A ) 이고 P(B|A)=\frac{P(B \cap A)}{P(A)}\rightarrow P(B\cap A)=P(B|A)P(A)\ 이고 P ( B ∣ A ) = P ( A ) P ( B ∩ A ) → P ( B ∩ A ) = P ( B ∣ A ) P ( A ) 이 고 P ( B ∩ A ) = P ( A ∩ B ) 이므로 P ( A ∣ B ) = P ( A ∣ B ) P ( B ) P ( A ) 이다 . P(B\cap A)=P(A\cap B)이므로\quad P(A|B)=\frac{P(A|B)P(B)}{P(A)}이다. P ( B ∩ A ) = P ( A ∩ B ) 이 므 로 P ( A ∣ B ) = P ( A ) P ( A ∣ B ) P ( B ) 이 다 . 또한,
P ( A ) = P ( A 1 ) + P ( A 2 ) + P ( A 3 ) + . . . + P ( A n ) 이고 , A 1 , A 2 , A 3 , . . . A n ∈ A 이면 P(A)=P(A_1)+P(A_2)+P(A_3)+...+P(A_n)이고,\\ {A_1,A_2,A_3,...A_n}\in A이면 P ( A ) = P ( A 1 ) + P ( A 2 ) + P ( A 3 ) + . . . + P ( A n ) 이 고 , A 1 , A 2 , A 3 , . . . A n ∈ A 이 면 P ( A 1 ) = P ( A ∩ A 1 ) = P ( A ∣ A 1 ) P ( A 1 ) P(A_1)=P(A\cap A_1)=P(A|A_1)P(A_1) P ( A 1 ) = P ( A ∩ A 1 ) = P ( A ∣ A 1 ) P ( A 1 ) 이다. 따라서
P ( A ) = ∑ i n P ( A ∣ A i ) P ( A i ) P(A)=\sum_{i}^{n}P(A|A_i)P(A_i) P ( A ) = i ∑ n P ( A ∣ A i ) P ( A i ) 이다.
Probability Distribution
Probability distribution assigns 혹은 A function mapping an event to a probability로 어떤 event가 발생하는 확률을 특정한 값으로 mapping 혹은 assign해주는 것이다.
Cumulative Distribution Function(CDF)
누적분포함수. 즉 discrete random variable에 대한 확률을 누적해 함수로 표현하는 것으로
F X ( x ) = P ( X ≤ x ) F_X(x)=P(X\le x) F X ( x ) = P ( X ≤ x ) 로 표현할 수 있다. CDF는 다음의 성질을 갖는다.
0 ≤ F X ( x ) ≤ 1 0\le F_X(x)\le 1 0 ≤ F X ( x ) ≤ 1 F X ( ∞ ) → P ( S ) = 1 F_X(\infin)\rightarrow P(S)=1 F X ( ∞ ) → P ( S ) = 1 F X ( − ∞ ) → P ( ∅ ) = 1 F_X(-\infin)\rightarrow P(\varnothing)=1 F X ( − ∞ ) → P ( ∅ ) = 1 P ( a ≤ X ≤ b ) = F X ( b ) − F X ( a ) P(a\le X\le b)=F_X(b)-F_X(a) P ( a ≤ X ≤ b ) = F X ( b ) − F X ( a ) P ( X > a ) = 1 − F X ( a ) P(X>a)=1-F_X(a) P ( X > a ) = 1 − F X ( a )
Probability Density Function(PDF)
CDF를 통해 discrete RV에 대해 함수로 표현하는 방법에 대해 알게됐다. 그렇다면 discrete가 아닌 continous RV에 대해서는 어떨까?
Continous RV에서 어떤 event X가 일어날 확률은 X 가일어난 E v e n t 모든 E v e n t \frac{X가 일어난 Event}{모든 Event} 모 든 E v e n t X 가 일 어 난 E v e n t P ( X ) = 0 P(X)=0 P ( X ) = 0
그럼 끝이냐? 아니지 똑똑이들은 가만히 있지 않는다. 앞에서 확률을 누적하여 함수로 표현하는 CDF를 이용해보자. 어느 작은 구간에 대해 생각해보자.
lim △ x → 0 P ( x < X ≤ x + △ x ) △ x = F X ( x + △ x ) − F X ( x ) △ x = 0 \lim_{\vartriangle x \to 0}\frac{P(x< X\le x+\vartriangle x)}{\vartriangle x}=\frac{F_X(x+\vartriangle x) - F_X(x)}{\vartriangle x}=0 △ x → 0 lim △ x P ( x < X ≤ x + △ x ) = △ x F X ( x + △ x ) − F X ( x ) = 0 어디서 본 모습이다. 미분의 정의인가...ㅎㅎ 맞는것같다. 어떤 똑똑이는 이것을 이렇게 표현한다.
f X ( x ) = lim △ x → 0 F X ( x + △ x ) − F X ( x ) △ x = F X ′ ( x ) f_X(x)=\lim_{\vartriangle x \to 0}\frac{F_X(x+\vartriangle x) - F_X(x)}{\vartriangle x}=F'_X(x) f X ( x ) = △ x → 0 lim △ x F X ( x + △ x ) − F X ( x ) = F X ′ ( x ) 이것이 Probability Density Function(PDF) 이다.
f X ( x ) = F X ′ ( x ) f_X(x)=F'_X(x) f X ( x ) = F X ′ ( x ) F X ( x ) = ∫ − ∞ x f X ( x ˉ ) d x ˉ = P ( X ≤ x ) F_X(x)=\int_{-\infin}^{x} f_X(\bar x)\, d\bar x=P(X\le x) F X ( x ) = ∫ − ∞ x f X ( x ˉ ) d x ˉ = P ( X ≤ x )
로 정리할 수 있다. 그리고 PDF는 다음의 성질을 갖는다.
f X ( x ) ≥ 0 F X ( x ) : n o n − d e c r e a s i n g 이므로 F X ′ ( x ) 의기울기 = f X ( x ) ≥ 0 f_X(x)\ge 0 \quad F_X(x): non-decreasing이므로\\F'_X(x)의 기울기=f_X(x)\ge0 f X ( x ) ≥ 0 F X ( x ) : n o n − d e c r e a s i n g 이 므 로 F X ′ ( x ) 의 기 울 기 = f X ( x ) ≥ 0
∫ − ∞ ∞ f X ( x ) d x = 1 = F X ( ∞ ) \int_{-\infin}^{\infin} f_X(x) dx=1=F_X(\infin) ∫ − ∞ ∞ f X ( x ) d x = 1 = F X ( ∞ )
위의 두 가지를 모두 만족해야 PDF를 정의할 수 있다.
P ( a < X ≤ b ) = ∫ a b f X ( x ) d x P(a<X\le b)=\int_{a}^{b} f_X(x)dx P ( a < X ≤ b ) = ∫ a b f X ( x ) d x
P ( X < a ) = P ( X ≤ a ) = ∫ − ∞ a f X ( x ) d x = F X ( a ) P(X<a)=P(X\le a)=\int_{-\infin}^{a} f_X(x)dx = F_X(a) P ( X < a ) = P ( X ≤ a ) = ∫ − ∞ a f X ( x ) d x = F X ( a )
Normal Distribution
함수를 다양한 모양으로 만들 수 있는데, 그 방법은 크게 두 가지가 있다. 하나는 공식의 파라미터를 바꿔주는 것이다. 다른 하나는 공식을 바꿔주는 것이다. PDF의 특정한 공식에 Normal Distribution, Beta Distribution과 같이 이름을 붙여준다. 그리고 거기에 들어가는 파라미터를 정의해준다.
대표적인 Normal Distribution에 대해 알아보자.
F o r m u l a : f ( x ; μ , σ ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 Formula:\quad f(x;\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} F o r m u l a : f ( x ; μ , σ ) = σ 2 π 1 e − 2 σ 2 ( x − μ ) 2 P a r a m e t e r : μ , σ Parameter: \mu,\ \sigma P a r a m e t e r : μ , σ M e a n : μ , V a r i a n c e : σ 2 \quad Mean: \mu,\ Variance:\ \sigma^2 M e a n : μ , V a r i a n c e : σ 2 Beta Distribution
Normal Dist와 다른 점은 Normal Dist은 0이 아닌 값으로 양 쪽으로 무한으로 가는 Long tail이 있고, Beta Dist는 0과 1사이에서 정해진다. 따라서 범위가 정해져있는 Distribution을 표현할 때 Beta Dist이 사용된다. 범위가 정해져있는 확률 을 모델링할 때 Beta Dist을 사용하면 유용하다.
F o r m u l a : P ( θ ) = θ α − 1 ( 1 − θ ) β − 1 B ( α , β ) , B ( α , β ) = γ ( α ) γ ( β ) γ ( α + β ) , γ ( α ) = ( α − 1 ) ! Formula:\quad P(\theta)=\frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha,\beta)},\quad B(\alpha,\beta)=\frac{\gamma(\alpha)\gamma(\beta)}{\gamma(\alpha+\beta)},\\ \gamma(\alpha)=(\alpha-1)! F o r m u l a : P ( θ ) = B ( α , β ) θ α − 1 ( 1 − θ ) β − 1 , B ( α , β ) = γ ( α + β ) γ ( α ) γ ( β ) , γ ( α ) = ( α − 1 ) ! P a r a m e t e r : α , β Parameter: \alpha,\beta P a r a m e t e r : α , β M e a n : α α + β , V a r i a n c e : α β ( α + β ) 2 ( α + β + 1 ) Mean: \frac{\alpha}{\alpha+\beta},\quad Variance: \frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)} M e a n : α + β α , V a r i a n c e : ( α + β ) 2 ( α + β + 1 ) α β Binomial Distribution
1.3장에서 압정을 던지는 Distribution으로 사용했던 Binomial Dist이다. Binomial Dist은 Discrete event에 대해 확률을 정의할 때 사용된다.
F o r m u l a : ( n k ) p k ( 1 − p ) n − k , ( n k ) = n ! k ! ( n − k ) ! Formula:\ {n \choose k}p^k(1-p)^{n-k},\ {n \choose k} =\frac{n!}{k!(n-k)!} F o r m u l a : ( k n ) p k ( 1 − p ) n − k , ( k n ) = k ! ( n − k ) ! n ! P a r m e t e r : P , n Parmeter:\ P,\ n P a r m e t e r : P , n M e a n : n p , V a r i a n c e : n p ( 1 − p ) Mean: np,\quad Variance: np(1-p) M e a n : n p , V a r i a n c e : n p ( 1 − p ) Multinomial Distribution
Binomial을 두 가지 케이스에 대한 확률분포를 다룬다면, Multinomial Dist은 Binomial dist를 일반화한 확률분포로 3가지 이상의 케이스에 대한 확률분포를 표현한다.
F o r m u l a : f ( x 1 , . . . , x k ; n , p 1 , . . . , p k ) = n ! x 1 ! . . . x k ! p 1 x 1 . . . p k x k Formula: f(x_1,...,x_k;n,p_1,...,p_k)=\frac{n!}{x_1!...x_k!}p_1^{x_1}...p_k^{x_k} F o r m u l a : f ( x 1 , . . . , x k ; n , p 1 , . . . , p k ) = x 1 ! . . . x k ! n ! p 1 x 1 . . . p k x k M e a n : E ( x i ) = n p i , V a r i a n c e : V a r ( x i ) = n p i ( 1 − p i ) Mean: E(x_i)=np_i,\ Variance: Var(x_i)=np_i(1-p_i) M e a n : E ( x i ) = n p i , V a r i a n c e : V a r ( x i ) = n p i ( 1 − p i )