"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 확률과통계 수업을 정리한 내용입니다.
Joint CDF of Bivariate RVs
이전까지 하나의 변수에 대한 확률에 대해서 다루었다. 만약 변수가 하나 더 늘어난다면 어떨까? 이번 강의는 그것에 대해서 다룬다.
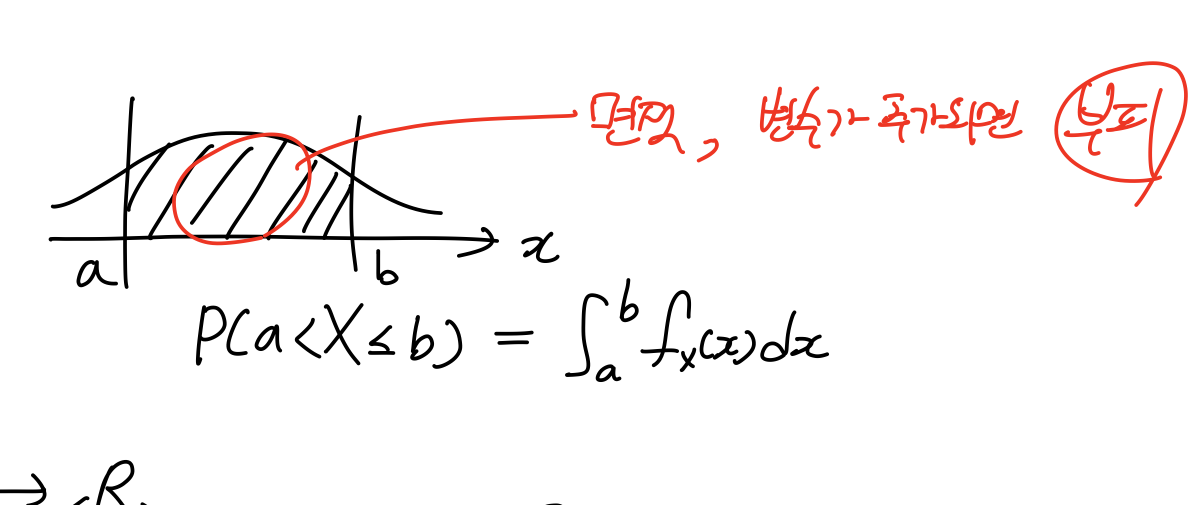
하나의 변수에 대한 cdf는 확률분포 그래프의 면적으로 나타낼 수 있었다. 변수가 하나가 추가된다면 우리는 2차원 상의 부피를 나타낼 것이라 예상할 수 있다.
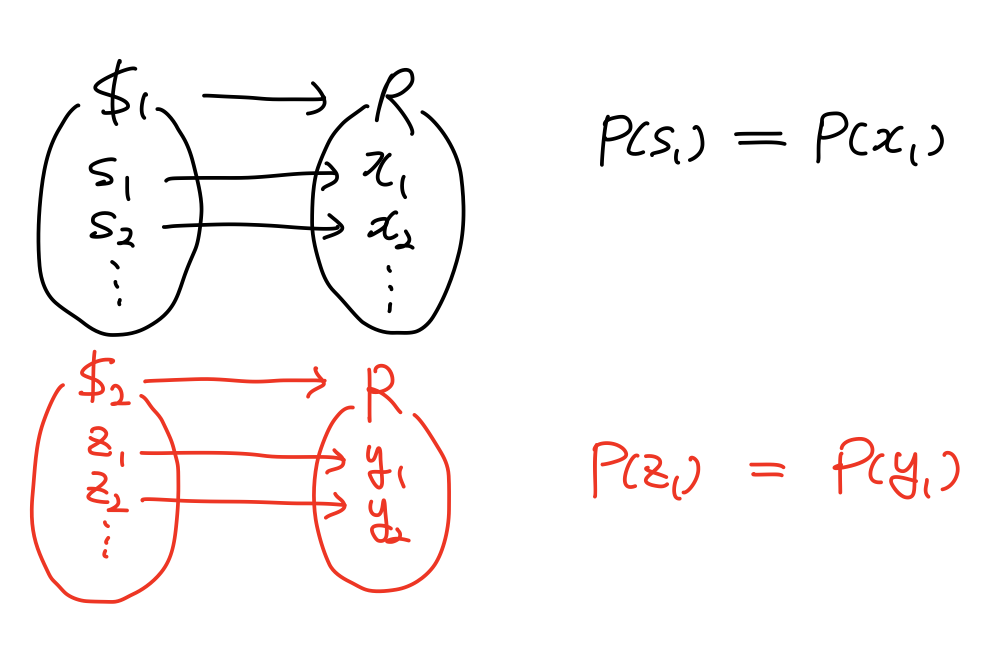
S1은 지금까지 다루었던 하나의 변수에 대한 sample space이다. 우리는 이것을 Real number의 Random variable에 매칭시키면 확률을 함수로 나타내었다. 변수가 하나 더 늘어나면, sample space와 real number를 늘리면 된다.
다만, 우리는 S1과 S2가 동시에 일어난다고 생각하면 sample space를 확장할 수 있다.

이것을 우리는 Joint Probability ( Density )라고 정의한다. 그리고 Joint CDF는 다음과 같이 표현할 수 있다.

Properties of Joint CDF
Joint CDF의 특성은 다음과 같다.
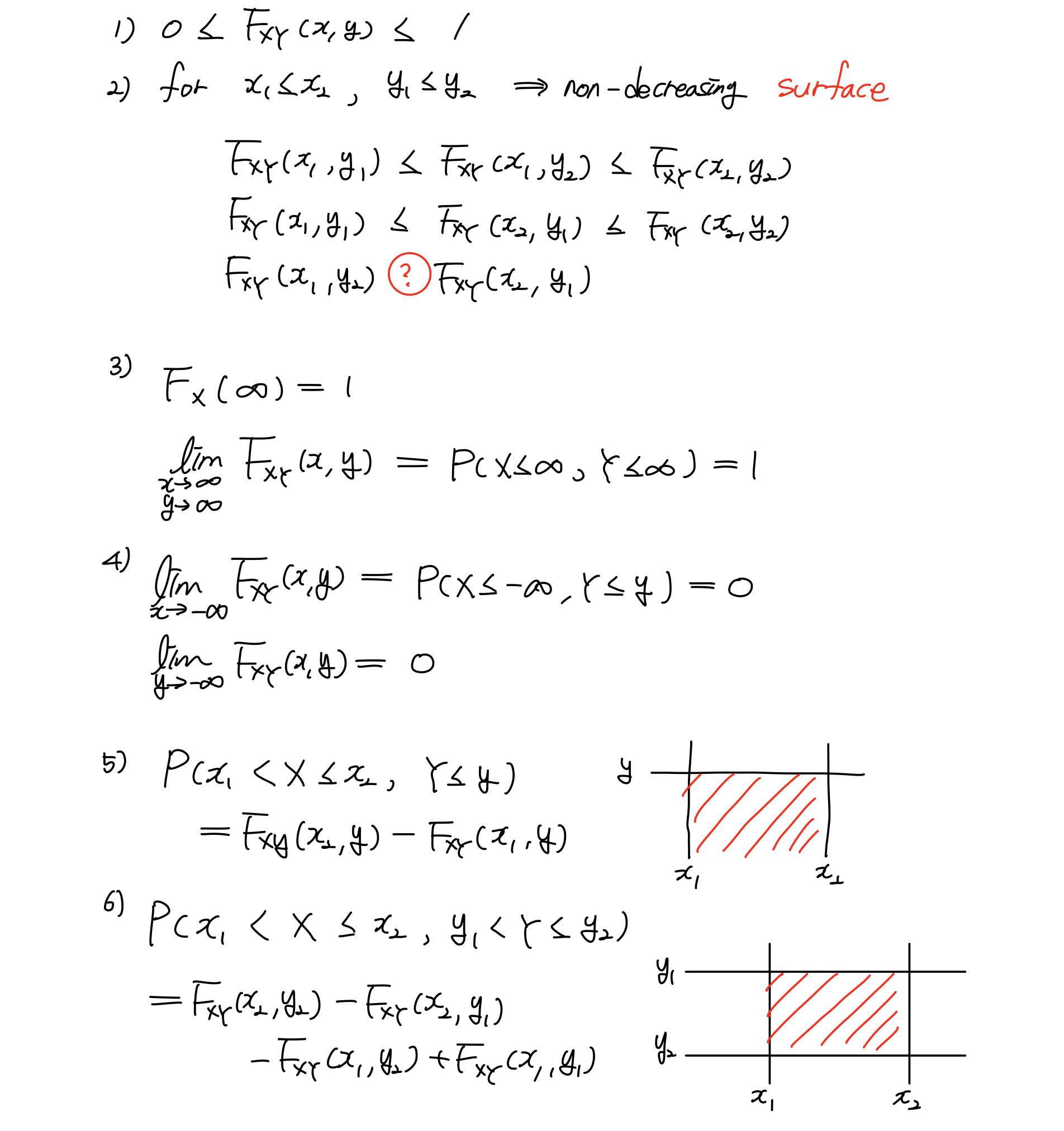
(2)에서 변수 하나일 때는 CDF는 non-decreasing line이었지만, 변수가 2개인 Joint CDF는 non-decreasing surface이다.
Marginal CDF
변수 2개를 다루는 Joint CDF에서 변수 1개인 CDF를 Marginal CDF라고 부른다. Marginal CDF는 해당하는 변수가 아닌 변수의 모든 값에 대해 다룬다.
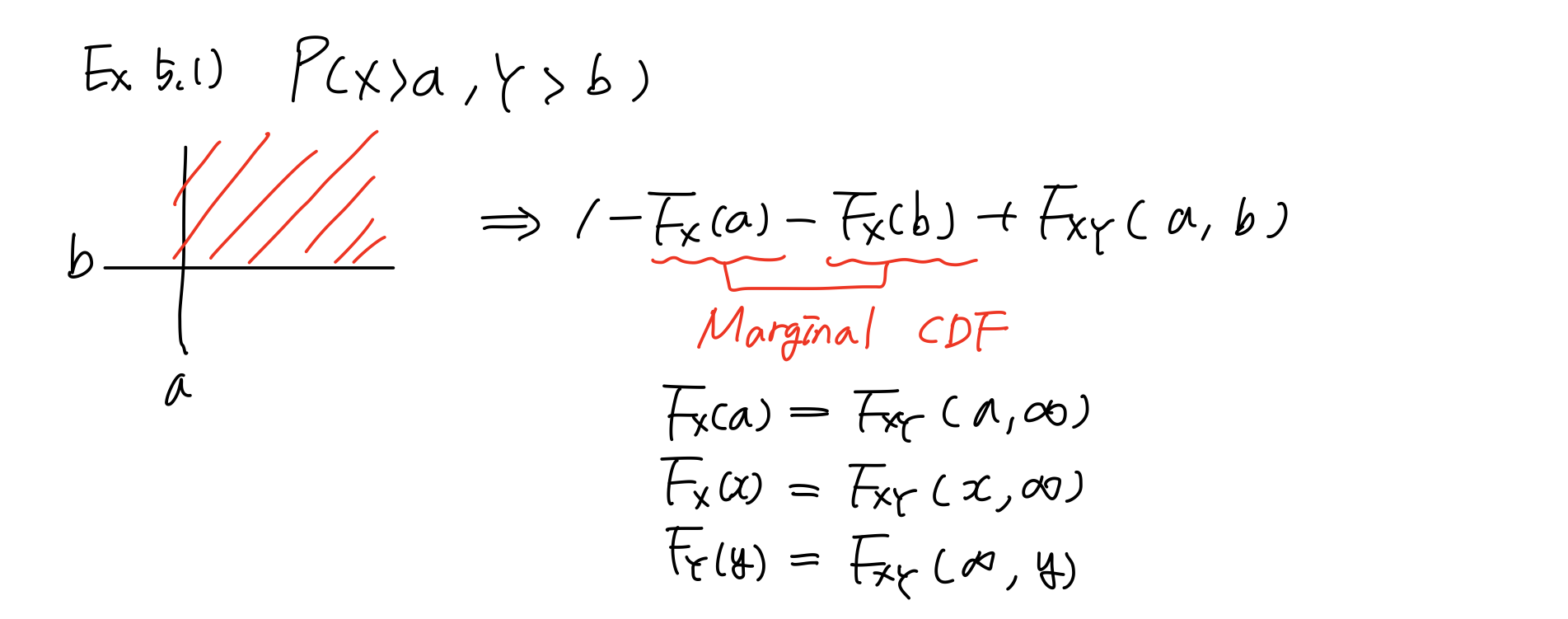
Discrete RVs
Discrete RVs에서 Multiple RVs는 어떨까? Discete RVs에 대해서는 Joint Probability와 많이 유사하다.
Properties
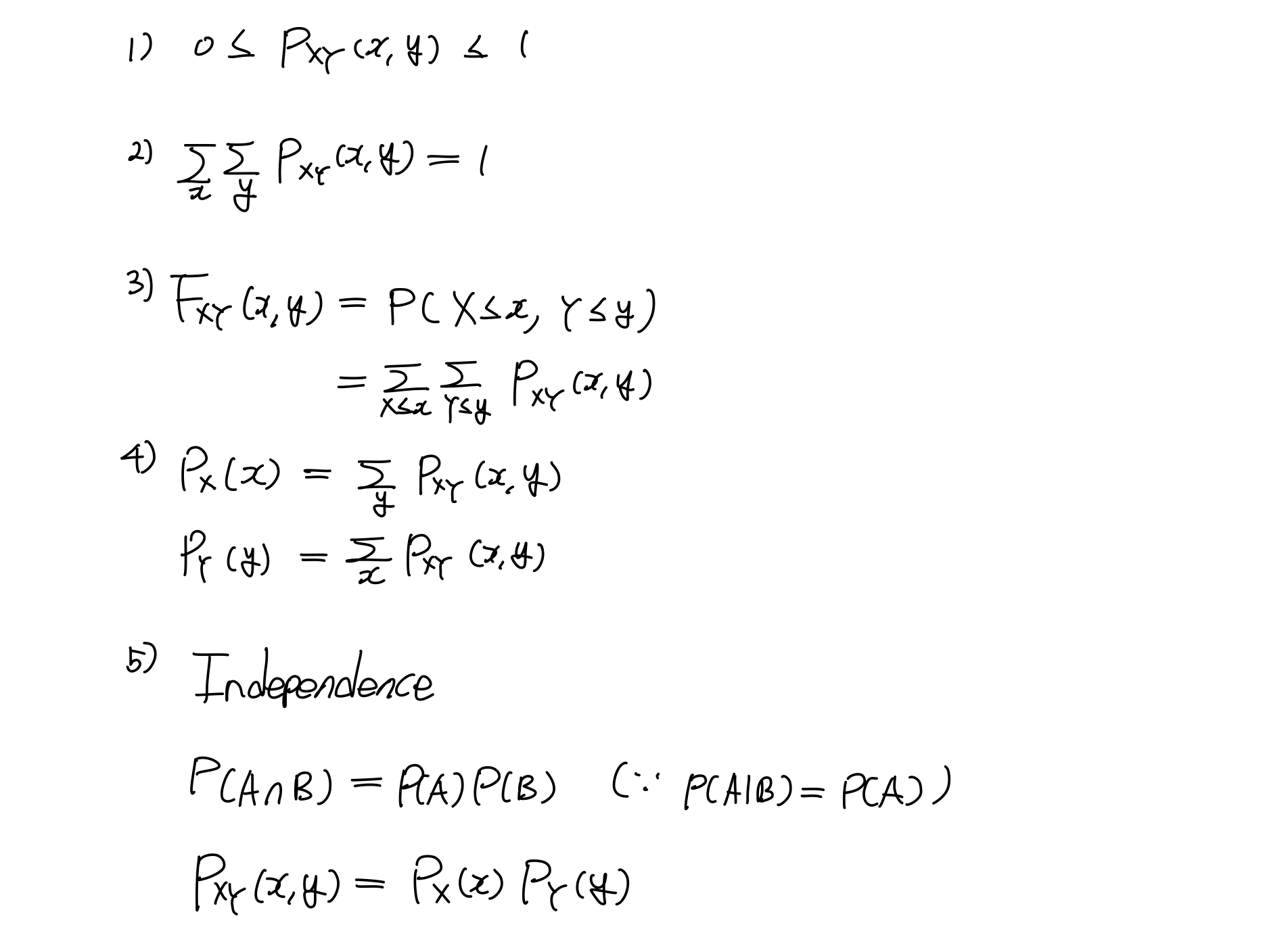
(5) Independence 에서 두 확률이 독립이라는 특징을 가지고 있기 때문에 Conditional Probability를 이용하면 위와 같이 정의할 수 있다.
Example
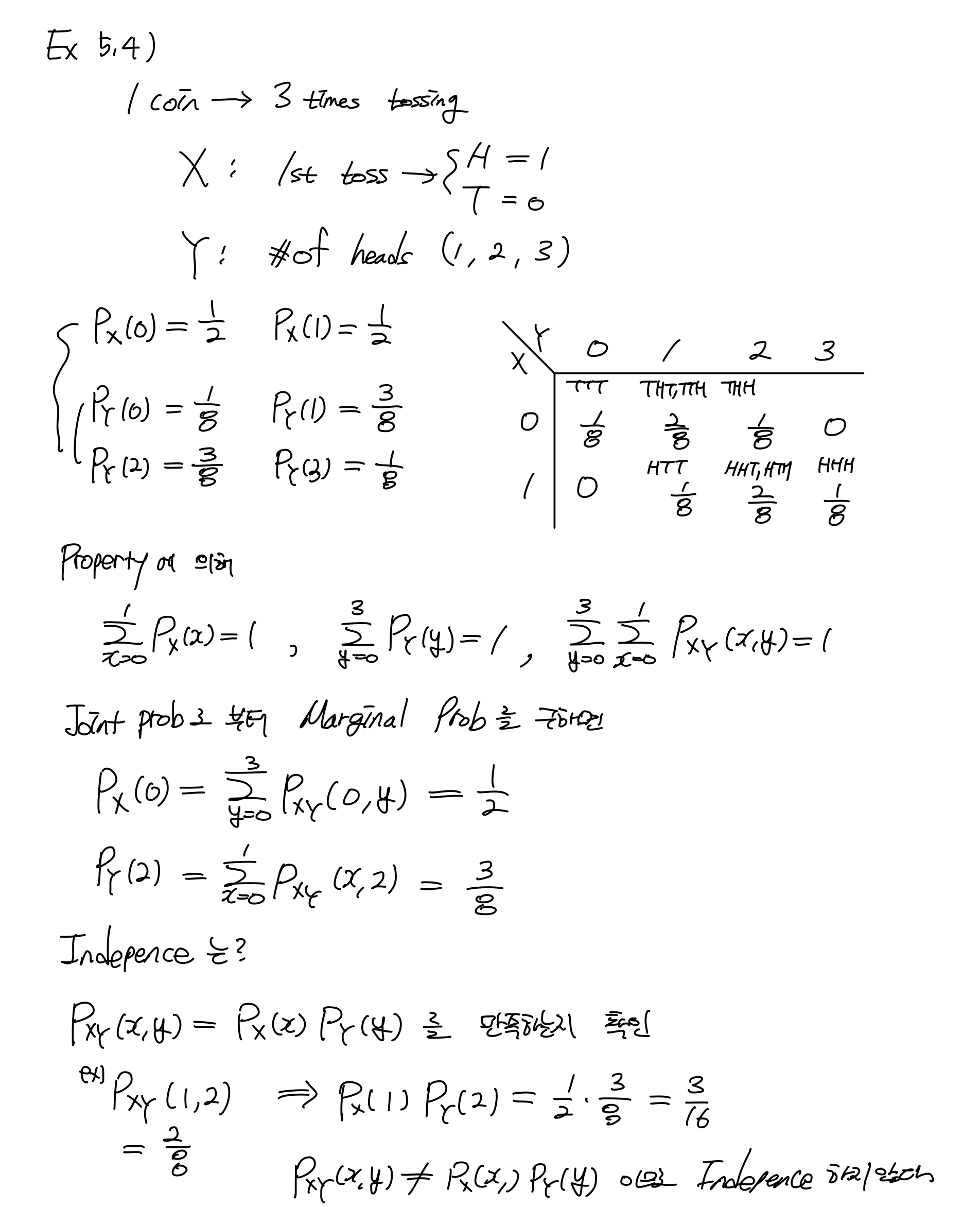
Continuous RVs
Continuous RVs에서 확률P를 정의할 수 없었던 것과 같이 Multiple RVs에서도 정의할 수 없기 때문에 우리 PDF를 이용해 정의한다.
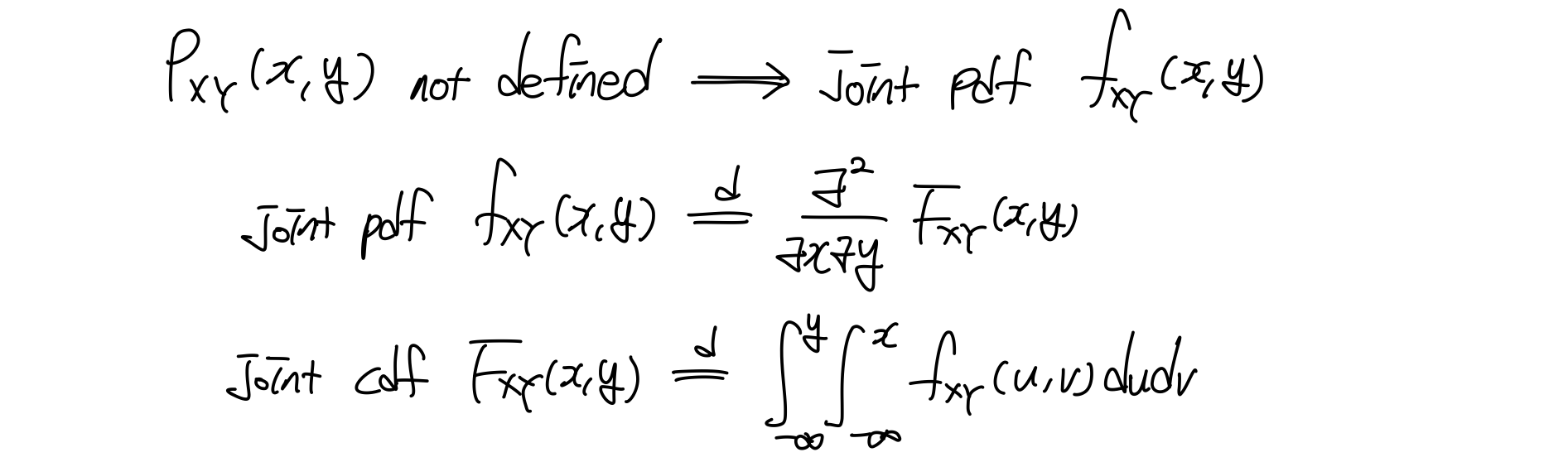
Properties
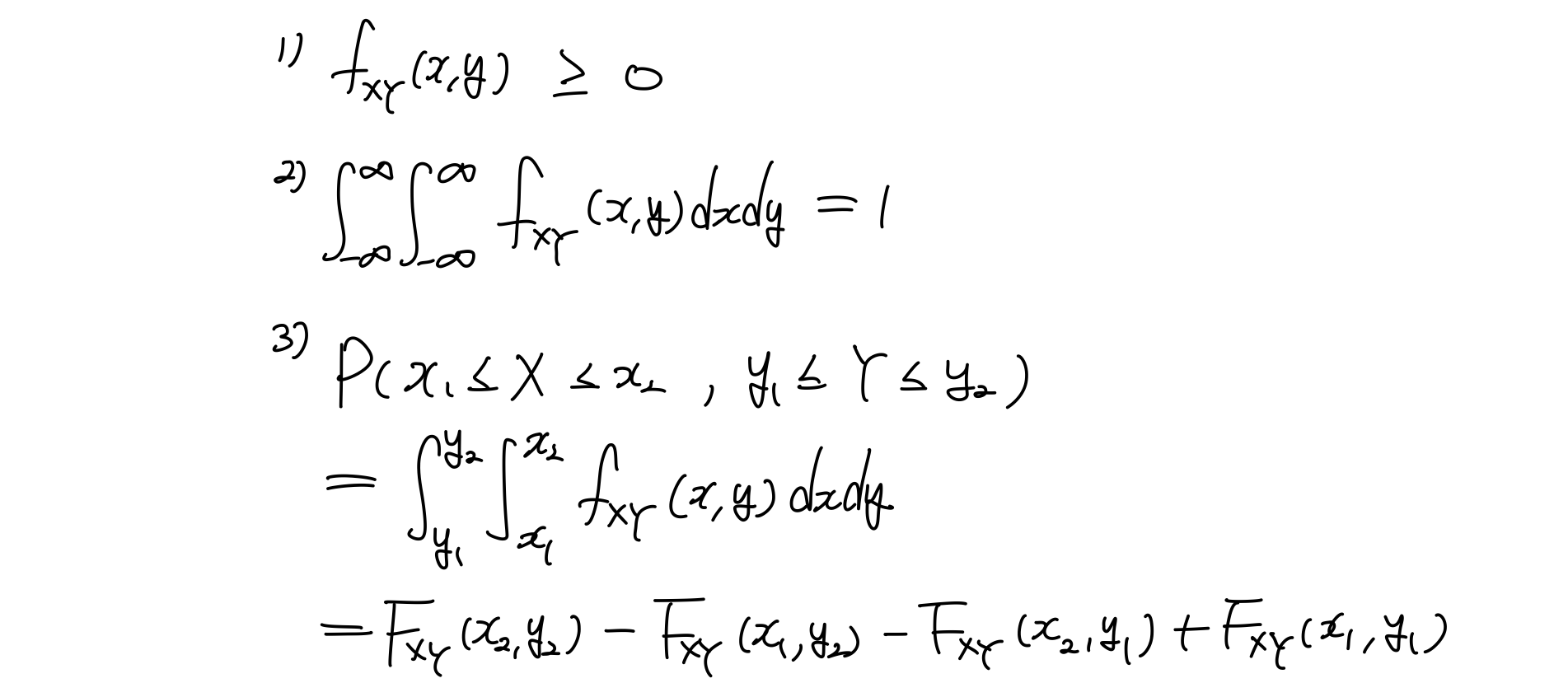
이때 적분의 의미에 대해 생각해보면, 변수가 1개인 PDF는 단위 길이당 확률값으로 정의했다. 그렇다면 변수가 2개인 Continous RVs의 Joint PDF는 어떻게 정의 내릴 수 있을까?
위와 같이 정의 내릴 수 있다. 따라서 적분할 때 dxdy를 곱해주면 우리는 확률 Probability를 구할 수 있다.
그림으로 나타낸다면, 밥그릇을 엎어 놓은 것처럼 dxdy 단위부피당 확률이 위로 솟아 하나의 surface를 만든 모양이라고 생각하면 된다.
