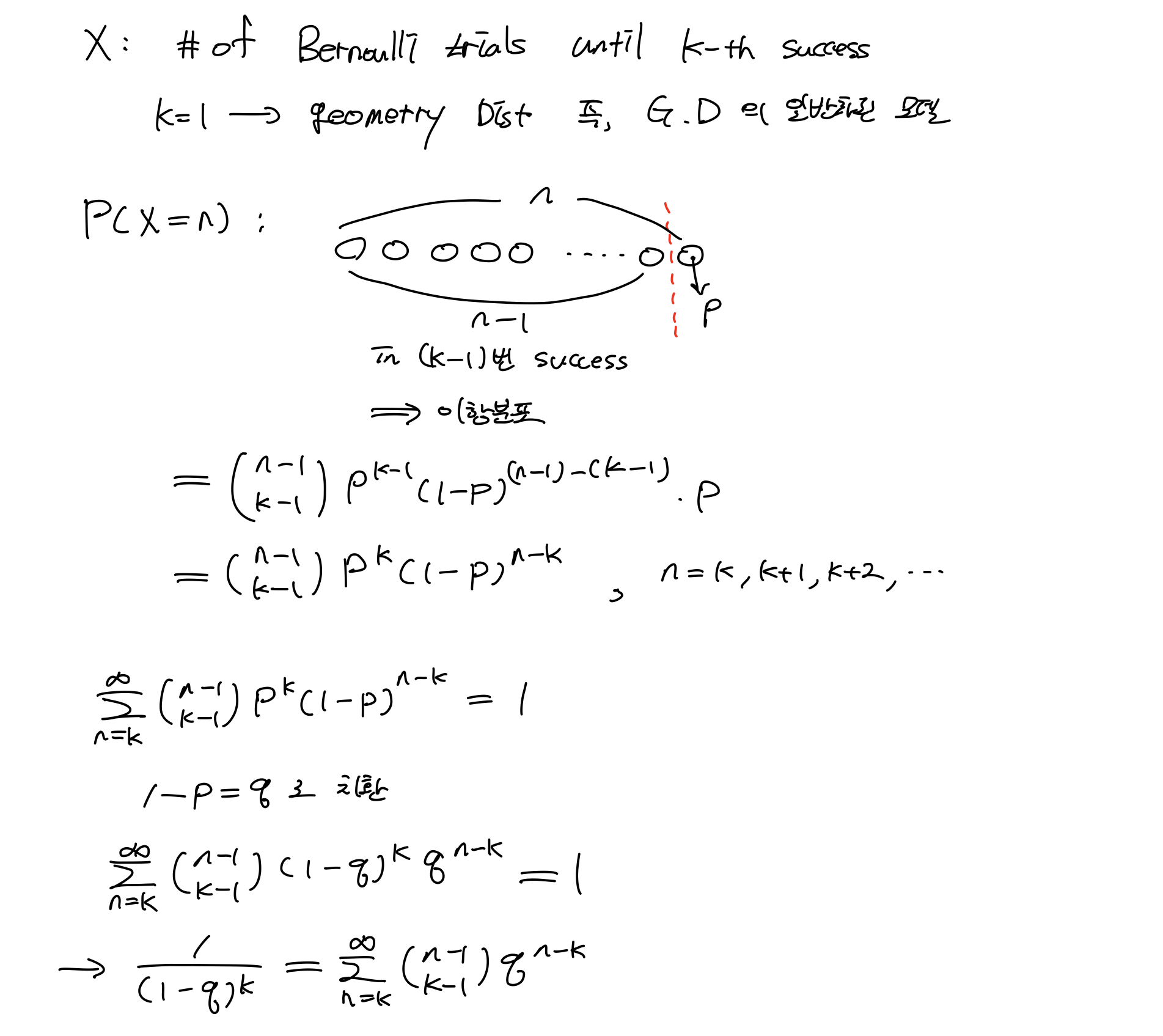"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 확률과통계 수업을 정리한 내용입니다.

Normal Dist (Gaussian)

정규분포 혹은 가우시안은 대표적인 연속 확률분포이다. Random variable의 정의는

X: continuous RVs for general cases

대표적인 예로, Noise가 있는 image sensor, audio signal, mobile channel이 있다. 기호는

이다.

연속 확률분포이므로 확률을 정의할 수 없기 때문에 PDF(Probability Density Function)로 표현하면 다음과 같다.

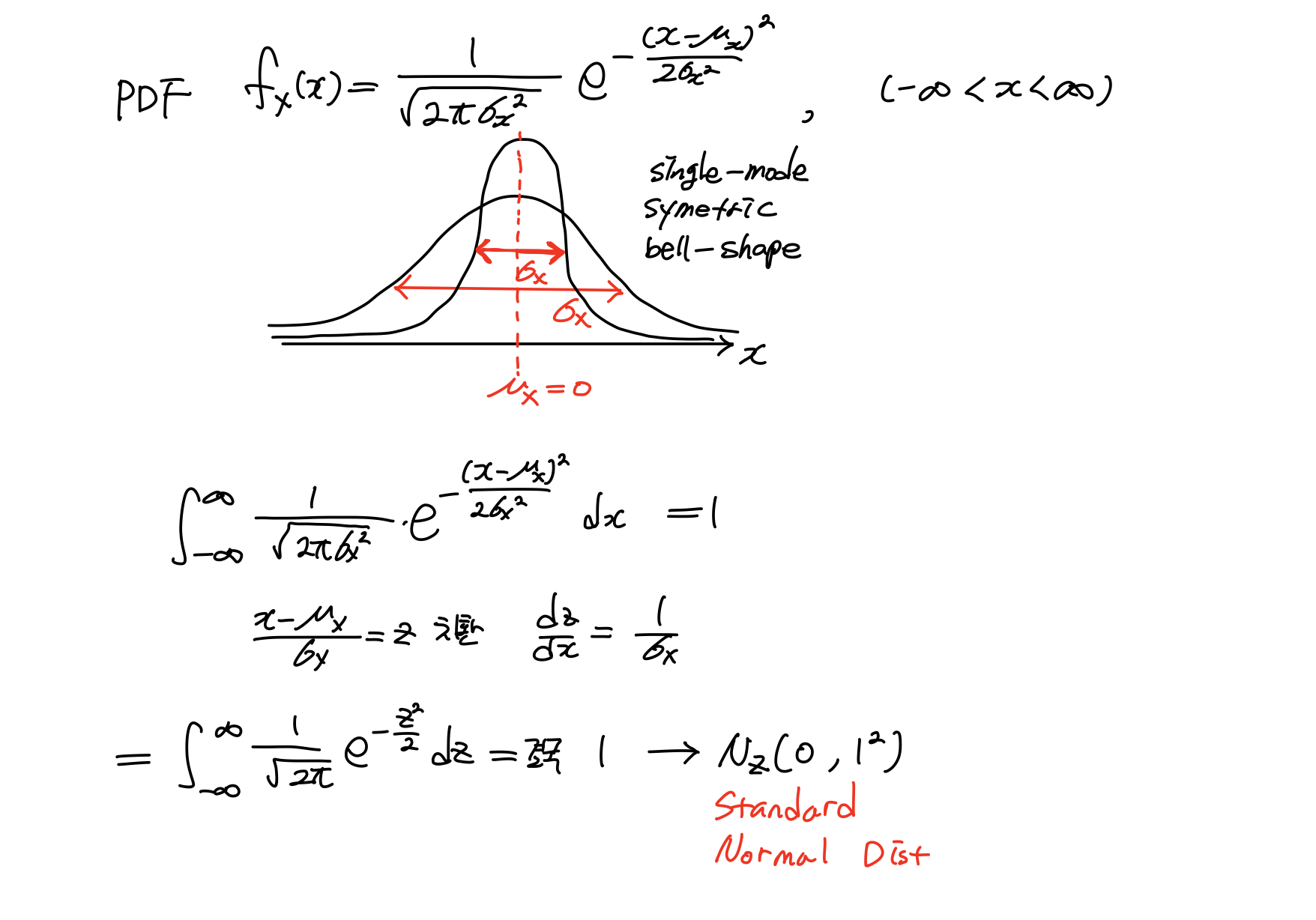
정규분포의 특징은 위로 솟은 봉우리를 mode라고 했을 때 single-mode, 평균을 기준으로 양쪽이 대칭인 symetric, 그리고 종 모양같다해서 bell-shape라고 한다. 평균을 기준으로 얼마나 분포되어 있는 정도를 나타내는 값으로 표준편차 $\sigma_X$로 표현한다.

또한, PDF가 성립하기 위한 조건으로 모든 영역($-\infin \infin$)에 대해 적분하면 1이어야 한다. 이게 진짜로 1이 나오는지 알아보자.

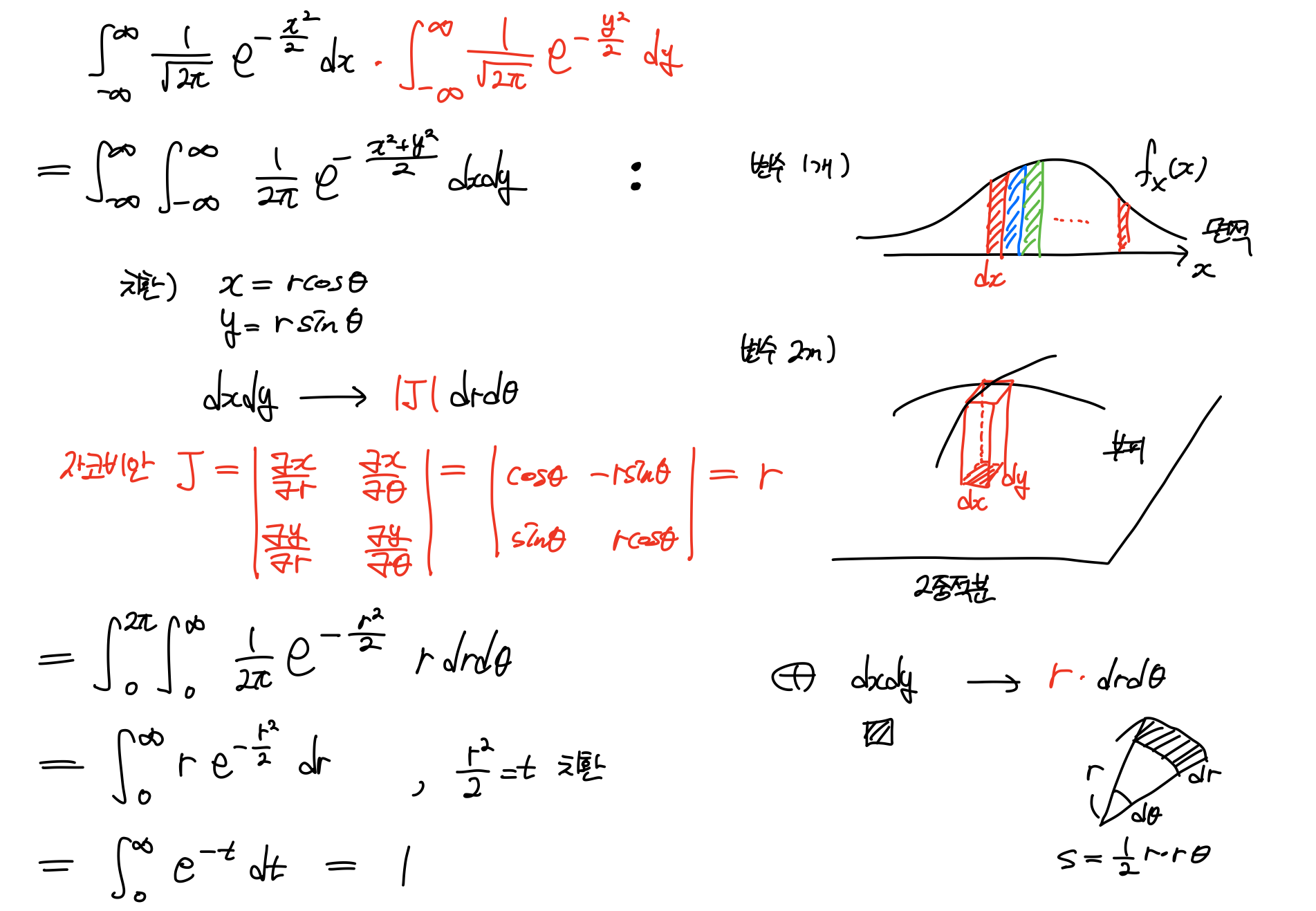
구하는 과정에서 자코비안 J의 개념이 나왔다. 이것은 면적을 나타내는 dxdy에서 극좌표 $drd\theta$로 변환할 때 필요한 일종의 parameter라고 생각하면 이해하기 쉽다. 결국 모든 영역에 대해 PDF를 적분하면 1이 나오는 것을 확인할 수 있다.

그럼 CDF(Cumulative Distribution Function)은 어떨까?

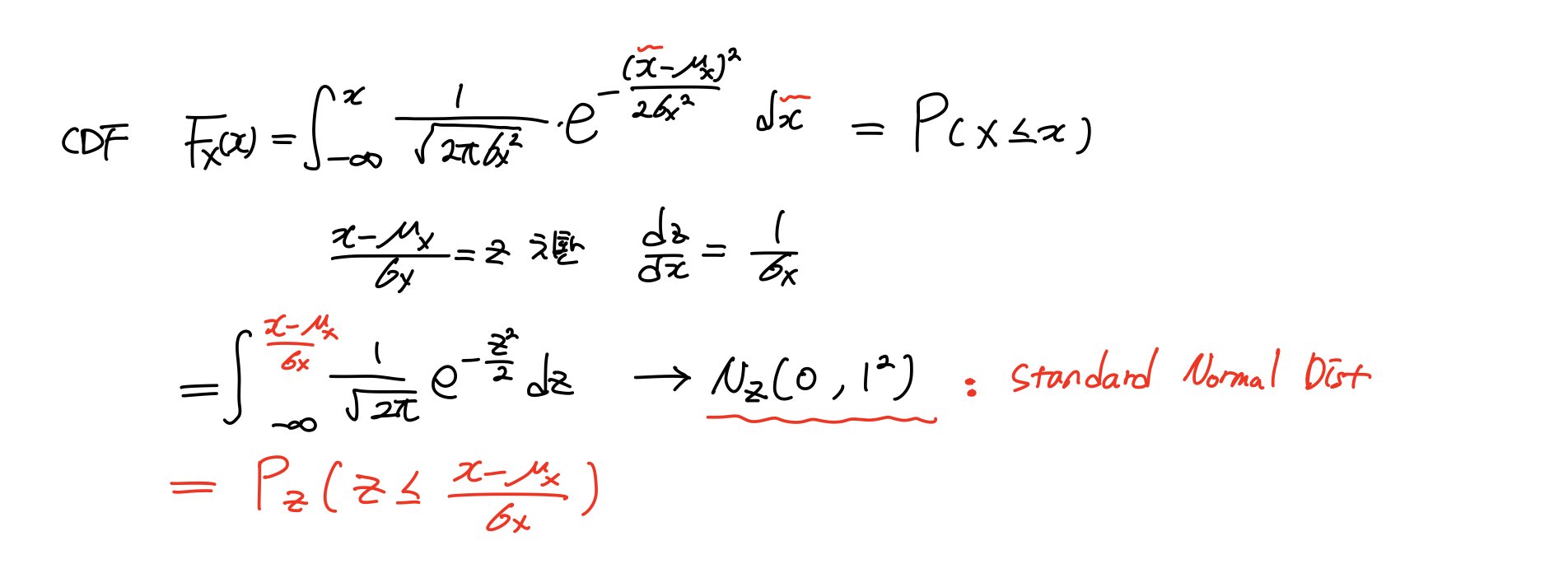
이때 평균이 0이고 분산이 1인 정규분포를 표준정규분포 Standard Normal Distribution이라고 한다. 표준정규분포는 이렇게 표현하기도 한다.

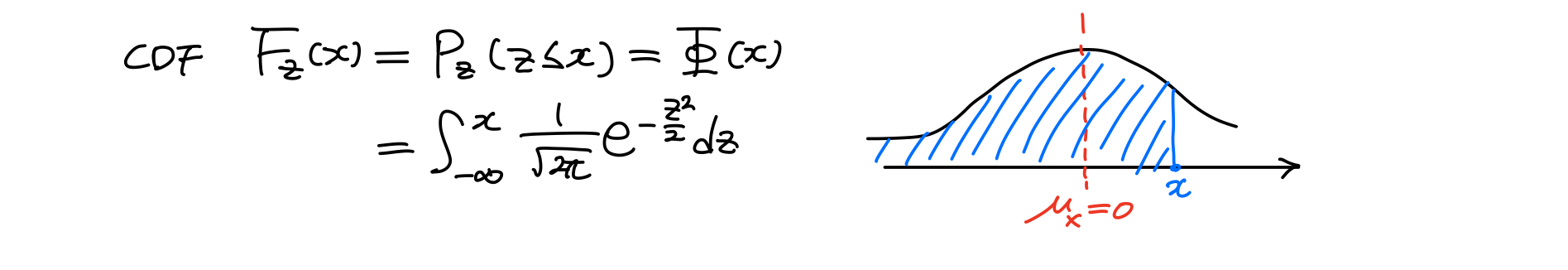
Example

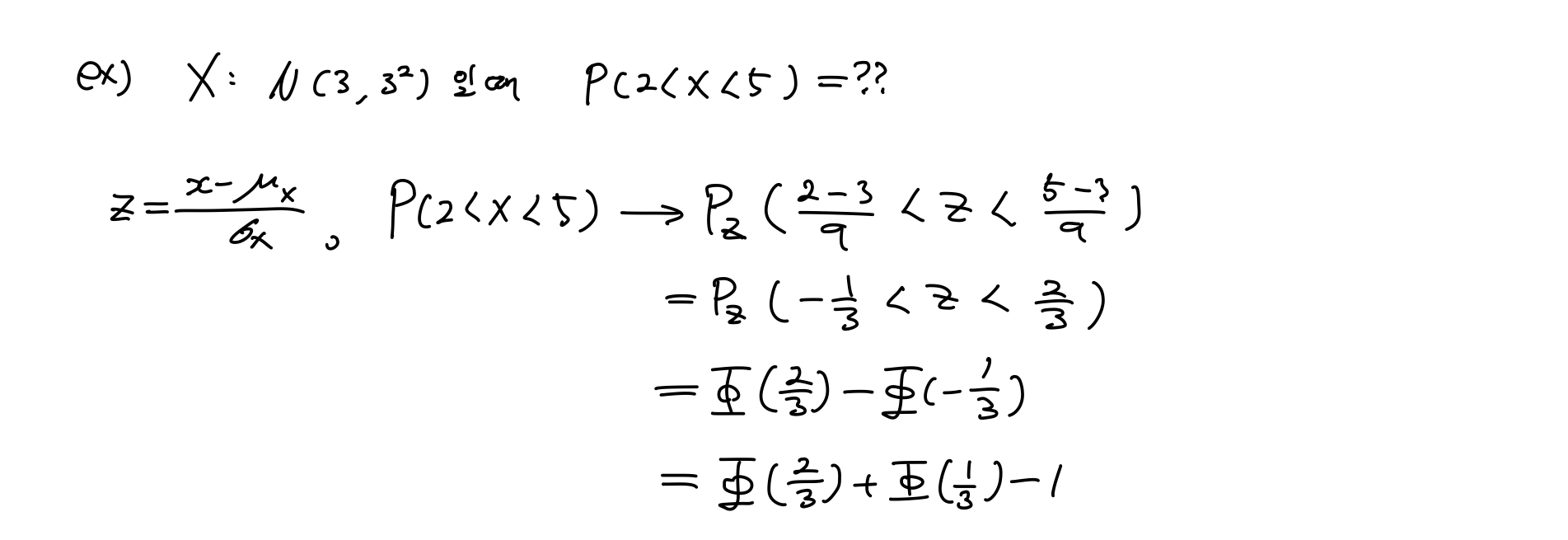
Approximation of Binormial Dist to Normal Dist

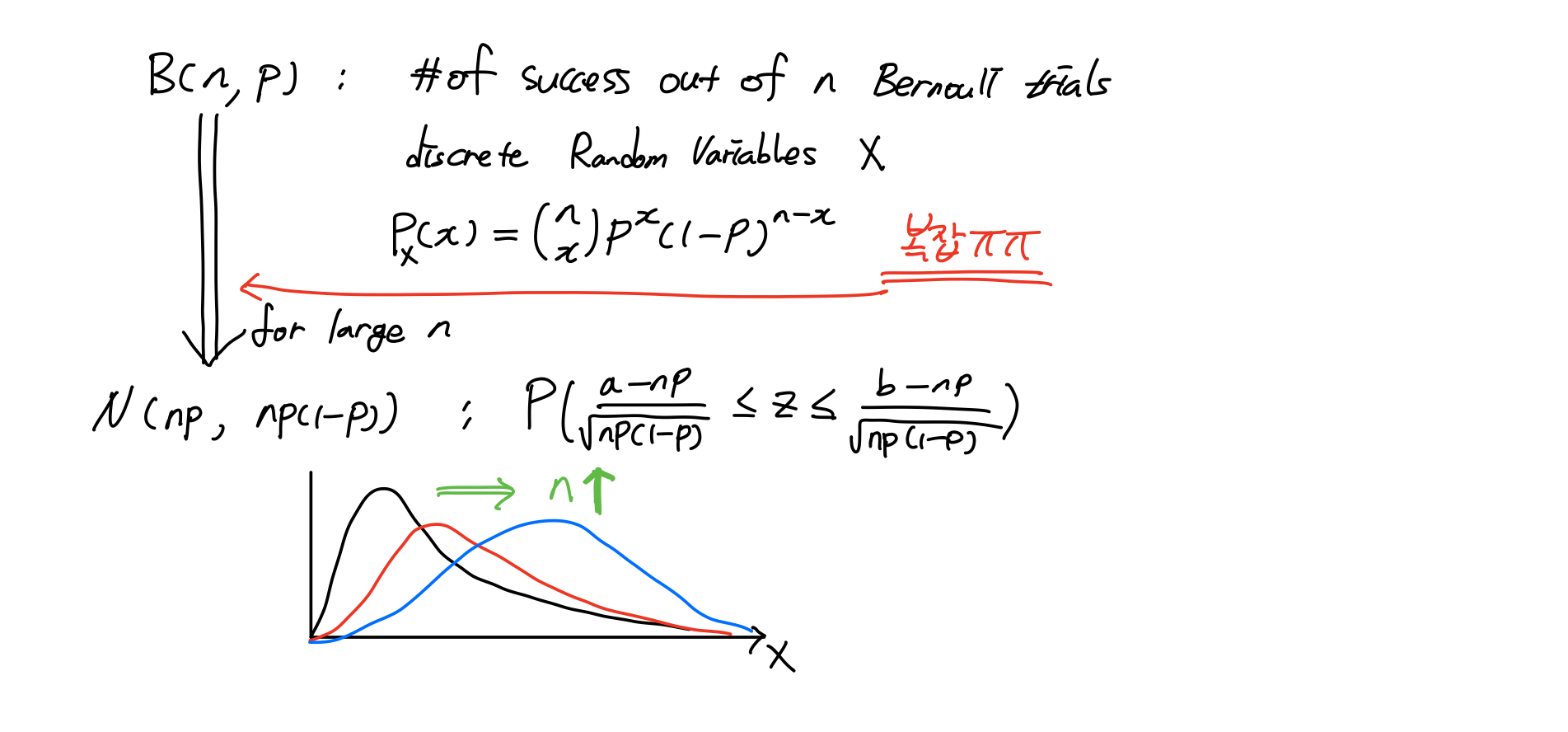
이산 확률분포인 Binormial Dist를 연속 확률분포인 Normal Dist으로 근사시키기 위해 Bernoulli trials n을 크게 늘리면 위와 같이 Normal Dist으로 근사화가 가능하다.

실제로는 discrete RVs에 대한 확률분포이지만 그 형태가 Normal Dist로 가까워 진다는 것이다. 팩토리얼 연산이 귀찮으니까 하는거다ㅎㅎ

Error function

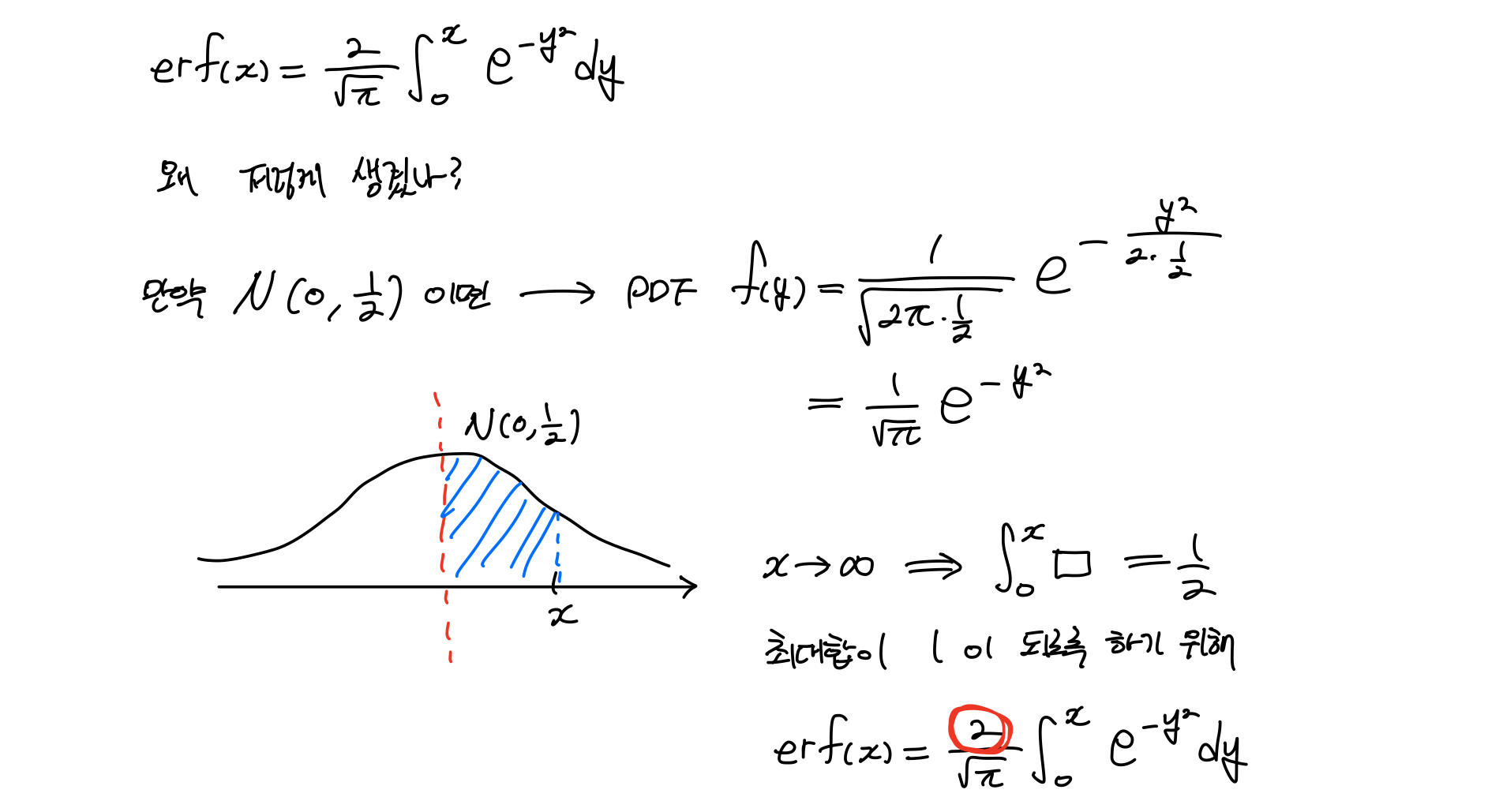
Error function의 pdf를 보면 보면 2가 곱해져 있는데, 이것은 평균이 0이고 분산이 1/2인 정규분포의 PDF형태를 보면 알 수 있다. 이때 0부터 x까지 정규분포를 적분한 형태에서 x를 $\infin$까지 늘리면 symetric한 특성에 의해 그 값은 1/2이 나온다. 그 결과를 1로 바꿔주기 위해 2가 곱해진 형태이다.

Complementary Error function

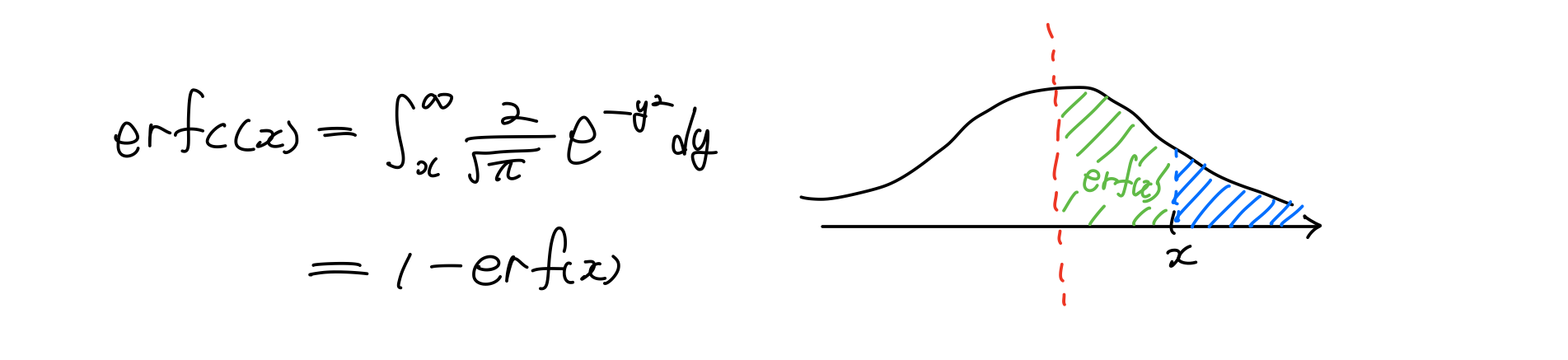
error function과 complementary Error func의 관계는 두 함수의 합은 항상 1/2이 된다는 것이다.

Standard Normal Dist와 Error function의 관계

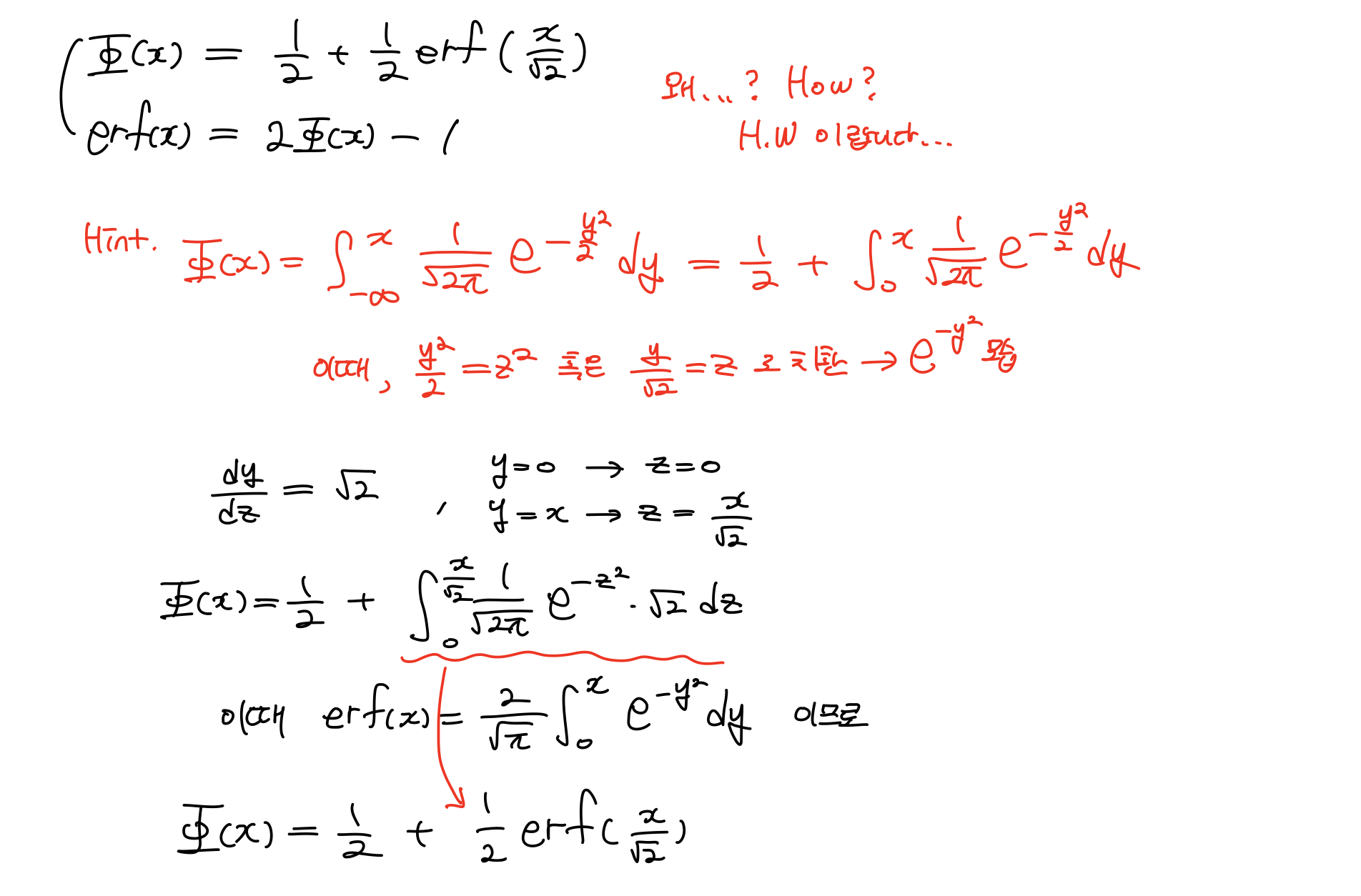
Pascal Dist