"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.

Review

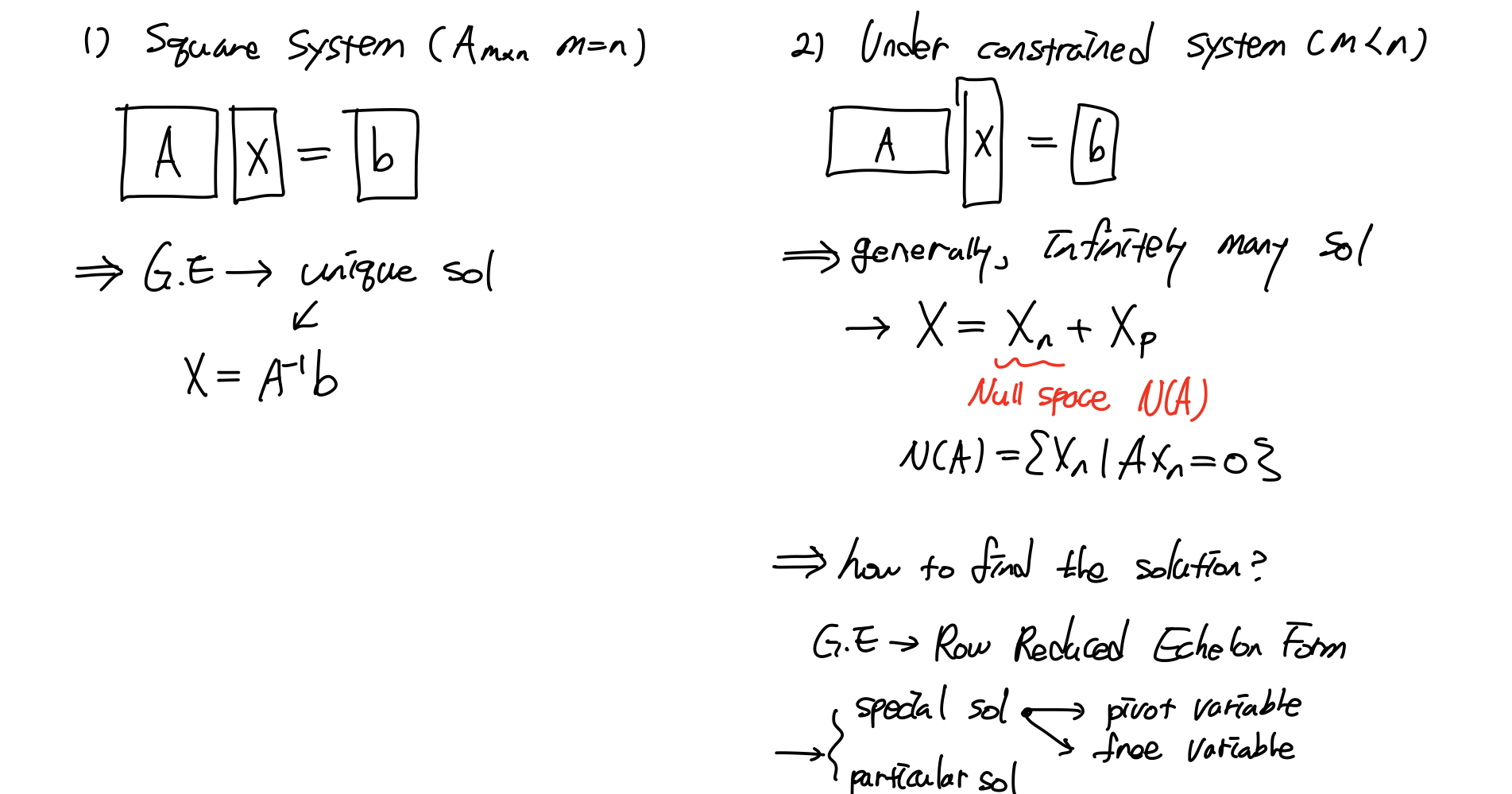
지금까지 우리는 Ax=b 연립방정식의 해를 구하는 과정을 배웠다. 처음에는 square system으로 주어진 방정식을 Gauss Elimination을 이용해 unique solutioin을 구했다. 만약 유일해가 존재하지 않는다면, 우리는 Vector Space를 이용해 해를 정의했다.

그 다음으로 미지수가 equation보다 많은 경우에 대해 다루어보았다. 일반적으로 이 경우는 무수히 많은 해를 갖는다. 해를 표현하기 위해 V.S 개념을 이용해 해를 정의할 수 있다. 그 방법은 Gauss Elimination을 취하고, Row Reduced Echelon Form U 형태로 만들어주어 Special solution과 Particular solution 형태로 해를 구했다.

이것은 Ax=0의 해를 나타내는 Null Space를 Special solution이라고 할 때, 그것을 Particular sol 만큼 평행이동시킨 Vector Space라고 생각할 수 있다. 그래서 Particular sol은 b와 관련이 있다.

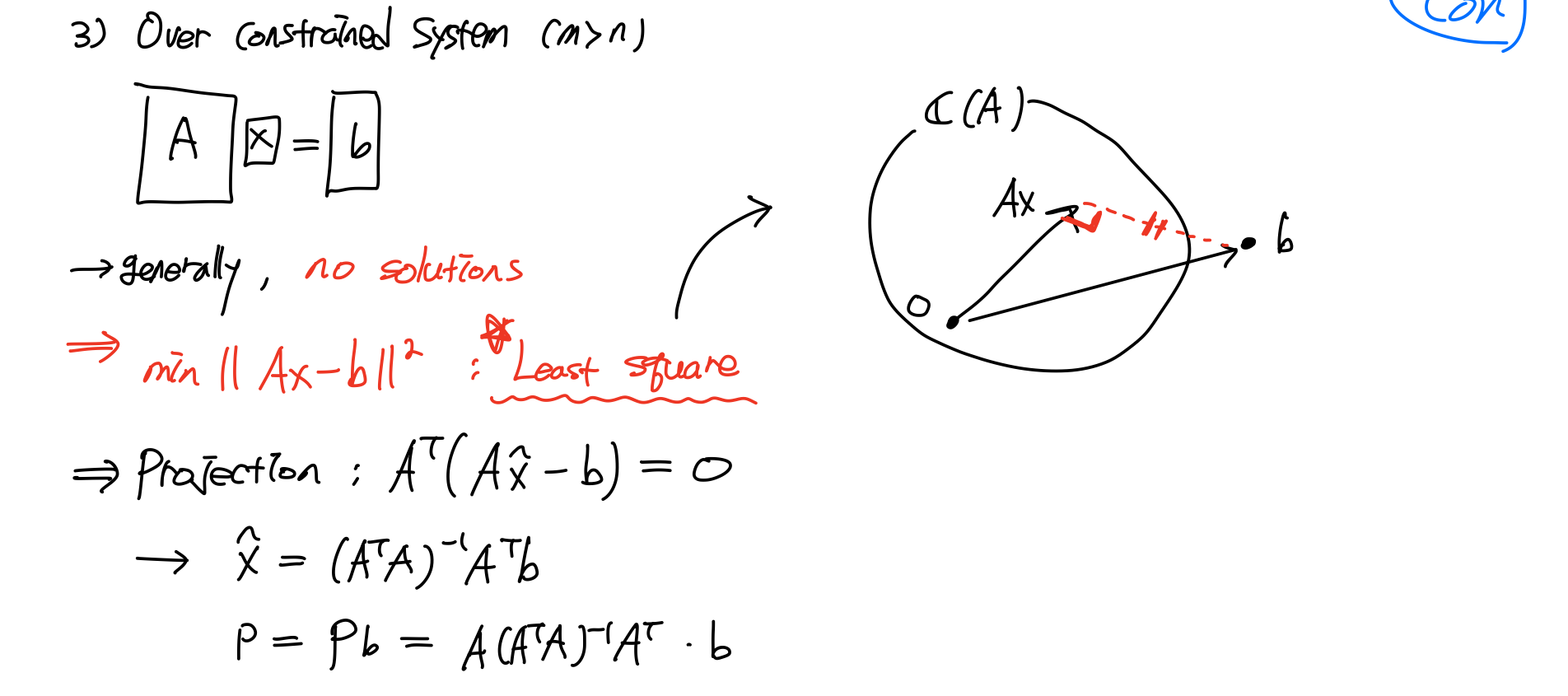
마지막으로 eqn이 미지수보다 더 많은 경우, Over contratined System에 대한 것이다. 이 경우는 사실 해가 존재하지 않는다. 그럼 끝? 아니죠~ 기하학적으로 생각했을 때 수 많은 방정식의 interaction을 모두 아우루는 최적의 해를 찾아야 할 것이다. 이를 Vector Space로 가져와 생각해보자.

위의 사진에서, 행렬A의 Column Space 속에 Ax는 원점을 지나는 어떤 곳을 나타내고 있을 것이다. b가 Column Space에 속해 있다면 해가 존재하겠지만, Column Space 밖에 존재하면 해가 존재하지 않는다. 그렇다면 b와 Column Space의 거리가 최소가 되는 특정 벡터를 구하는 것이 최적의 해를 구하는 것일 것이다. 이것이 Least Square이다.

이때 벡터 b에서 Column Space에 수직으로 발을 내리는 Projection해야 한다. 이때 수선의 발이 내려진 점을 $A\hat{x}$이라 표현하면, 그 수선의 발은 벡터로 $A\hat{x}-b$이고 Column Vector $A^T$와 수직이다.

Projection Matrix

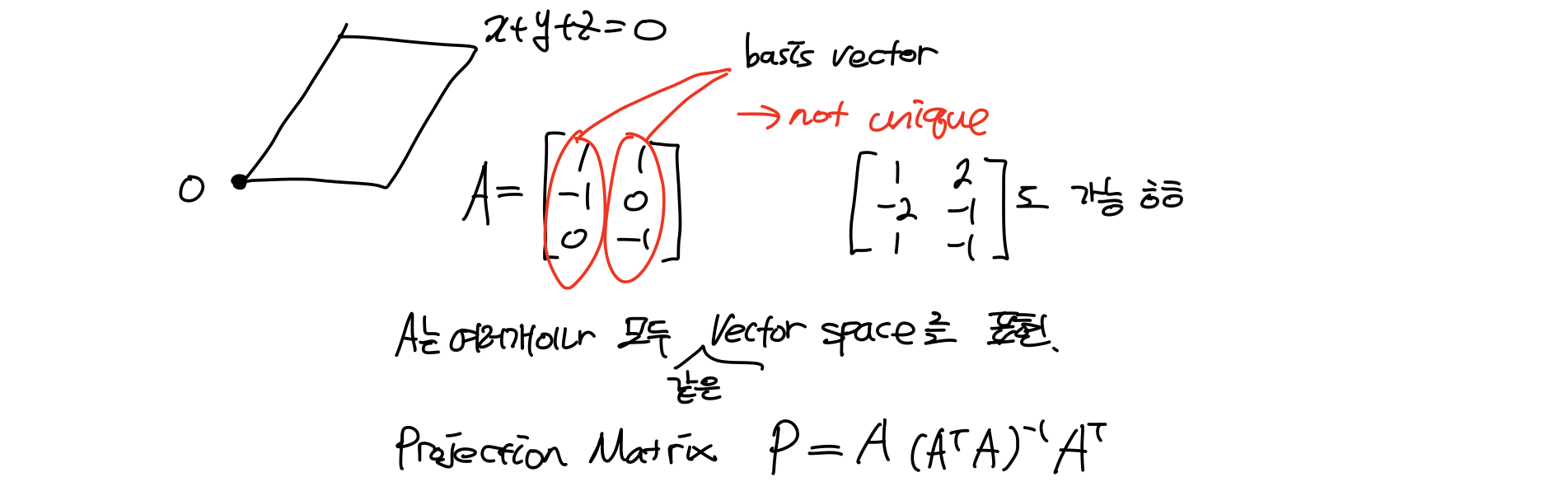
어떤 3차원 공간에 평면 x+y+z=0 이 존재한다. 이 평면을 나타내는 linearly independent vector로 이루어진 행렬A가 있다. 이때! 이 column vector는 basis vector이고, 이는 Vector Space에 대해서는 not unique하다. 따라서 여러 형태로 만들 수 있는 행렬A는 모두 같은 V.S를 표현한다. 이를 이용한 Projection Matrix는 행렬A를 이용해 표현할 수 있다.

만약 basis vector가 서로 Orthogonal 하다면?

Orthogonal basis vector

X를 basis vector를 이용해 표현할 수 있고, 만약 Orthogonal 특징을 갖는다면 쉽게 표현할 수 있다. 이를 이용해 Projection Matrix를 구하는 것이 용이하다.

그럼 Orthgonal basis vector는 어떻게 구할까?

If given Independent vectors $a_1, a_2,...a_n$, find the orthogonal basis vectors.
$\rightarrow$ Gram-Schmidt Orthogonalization

Gram-Schmidt Orthgonalization

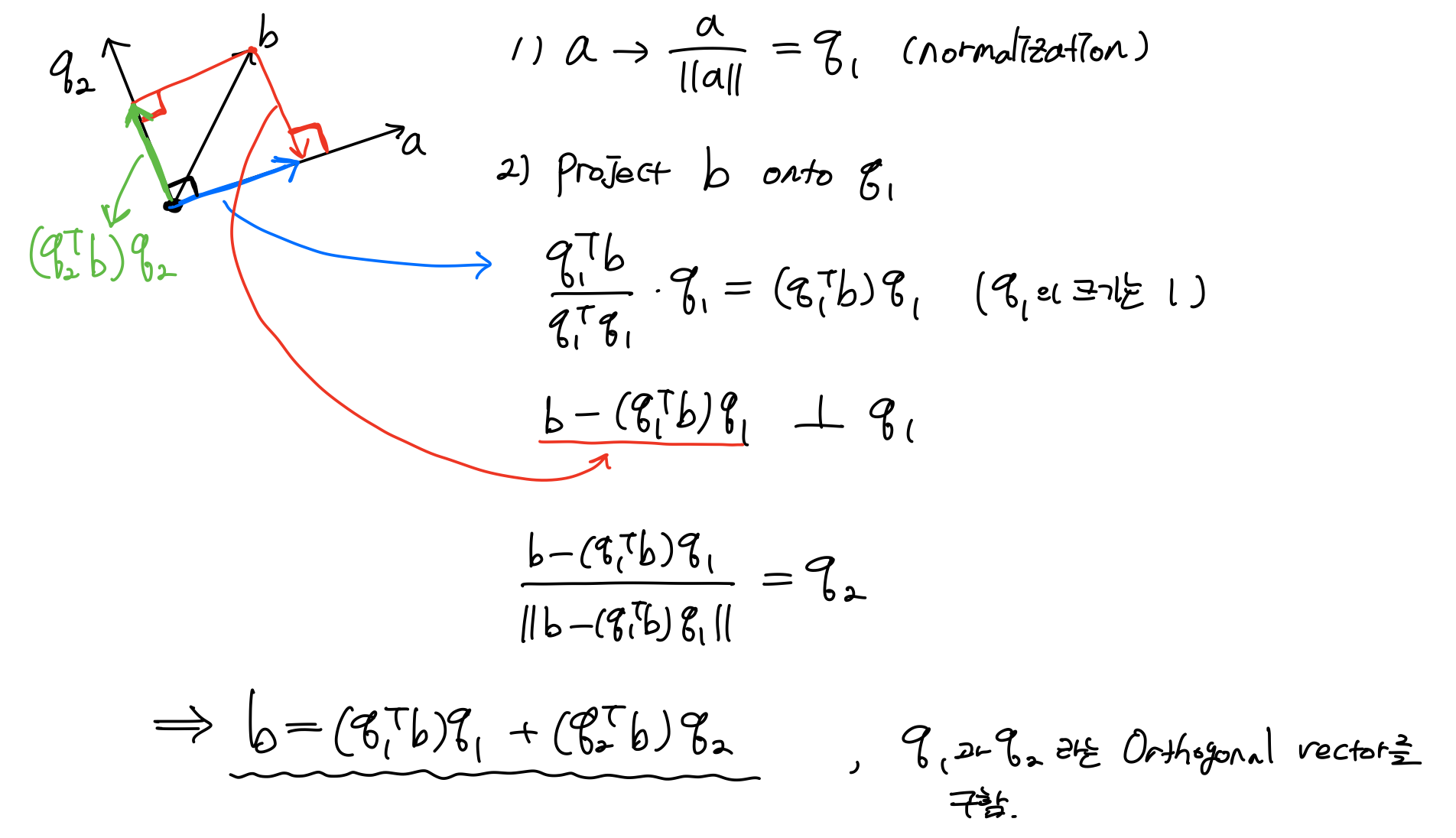
주어진 independent vector를 normalization으로 구한 크기가 1인 vector를 이용해 orthogonal vector를 구한다. 그리고 두 번째 independent vector($a_2=b$)를 새롭게 구한 vector에 projection을 한다. 이런 방식으로 vector b를 위와 같이 표현한다.

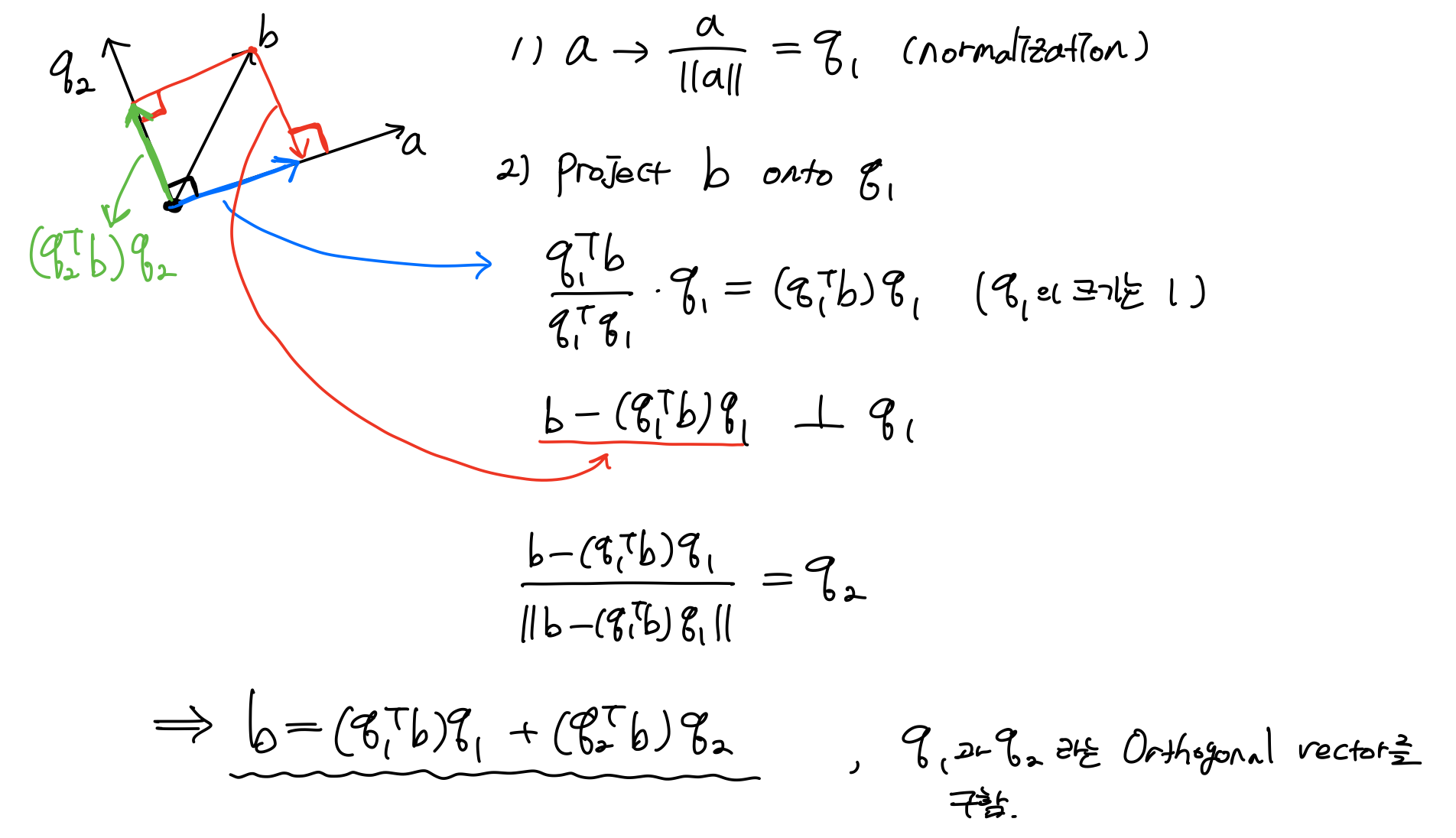
그리고 같은 방식으로 새로운 orthogonal vector $q_3$를 구해 vector C를 표현할 수 있다.

정리하면 아래와 같다.

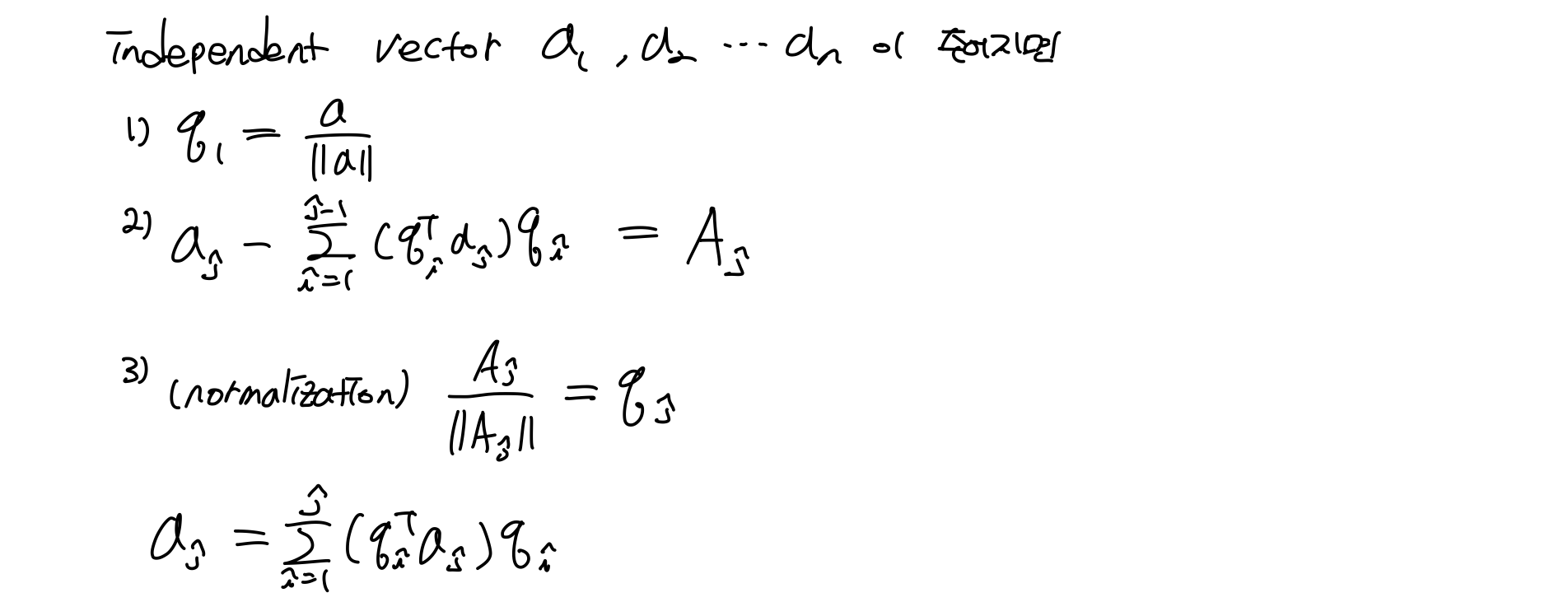
Projection $\rightarrow$ Least Square

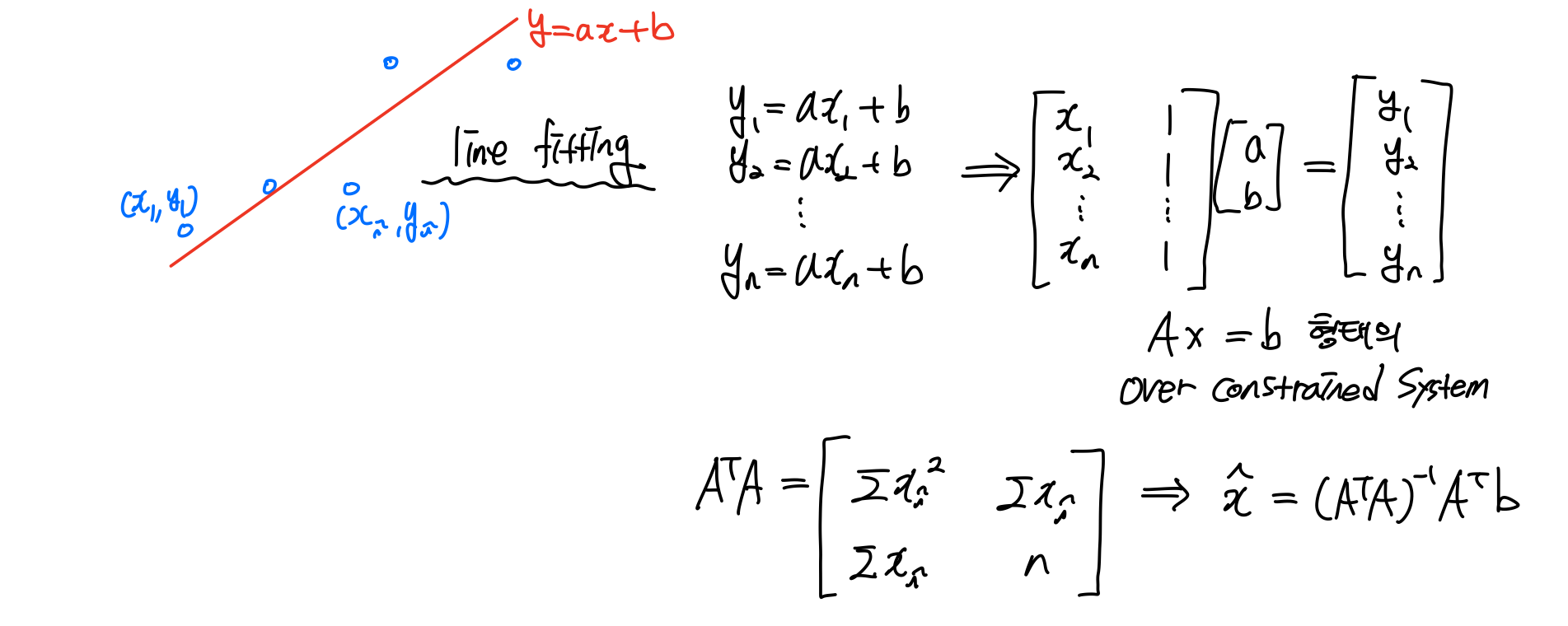
주어진 데이터에는 noise와 측정 error가 존재하기 때문에 모든 데이터를 아우르는 fitting이 필요하다. line fitting을 예로들면, 위와 같이 Over constrained System 형태를 띄고 있다. 이때 우리는 Projection 개념을 이용해 미지수를 구할 수 있다.

이를 수학적인 관점에서 미분을 이용해 구한다면,

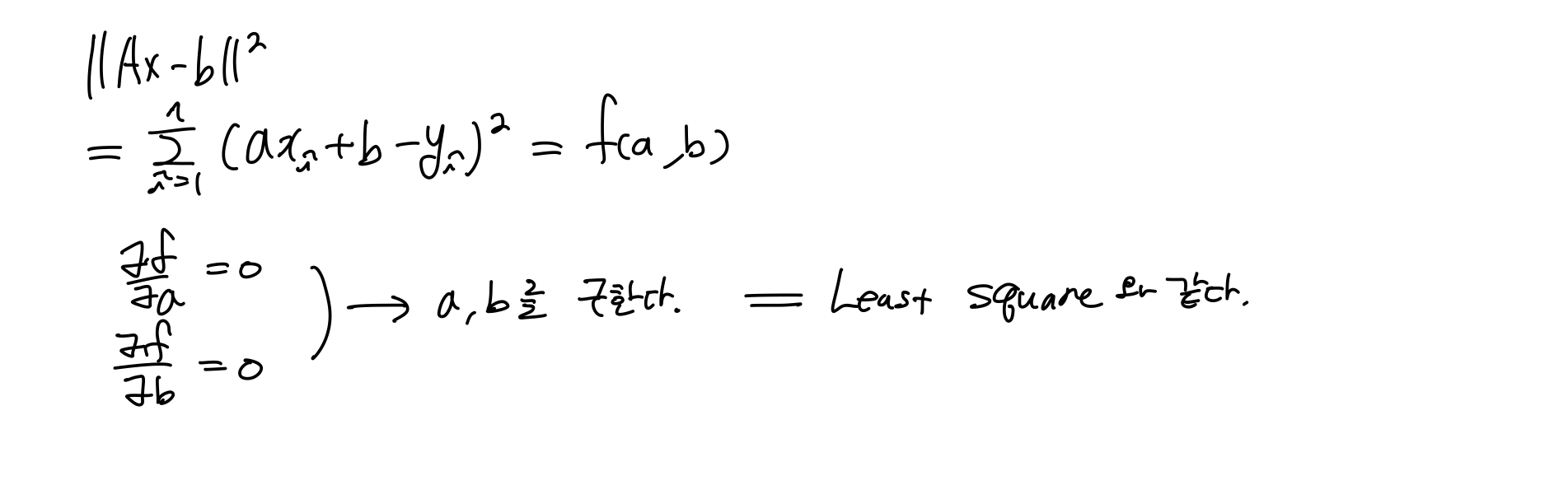
결국 두 방법은 모두 같은 해를 나타낼 것이다.