"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.
Function Space (Hillbert Space)
expand vector space to funtions
Vector space Hillbert space
이때 Vector space는 finite dimension이고, Hillbert space는 infinite dimension이다.
함수 x(t), y(t) H ()이면,
x(t) + y(t) H 이고,
x(t) H 이다.
우리는 vector를
Inner product
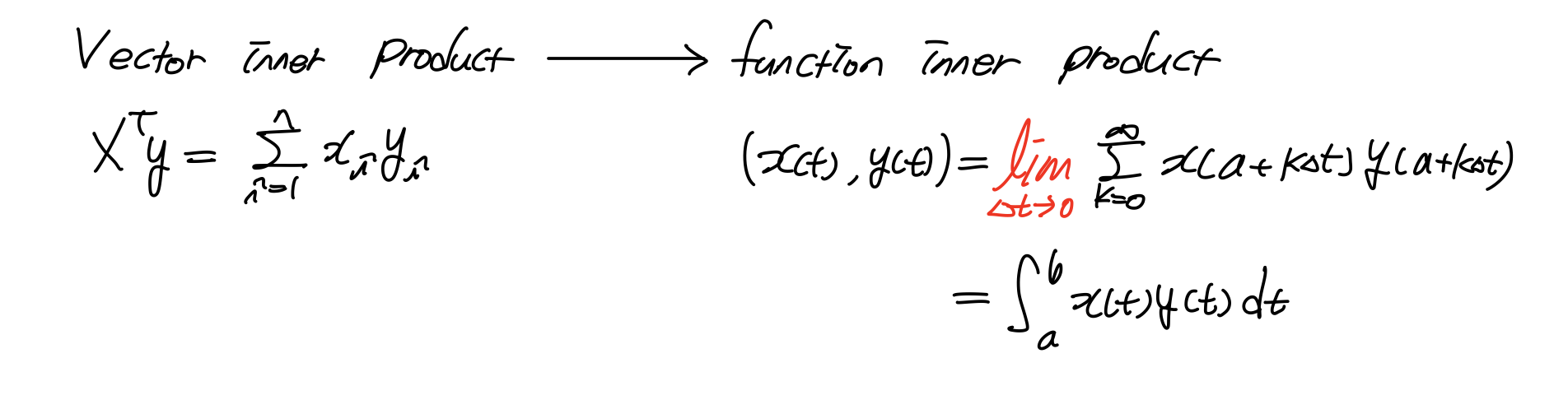
vector space에서 내적과 같이 function space에서 내적은 위와 같이 무한급수를 Integration으로 바꾸어 주는 것이다.
Orthogonality
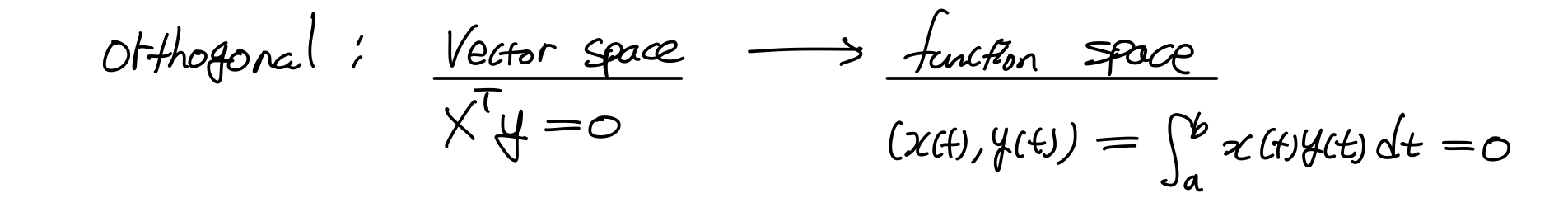
Vector space와 같이 내적이 0이 될 때, 두 함수는 서로 orthogonal 하다.
Basis function

Vector space에서 linear combination을 이용해 basis vector를 구한 것과 같이 function space에서 basis function은 series라고 한다.
Orthogonal + Basis = Orthonormal
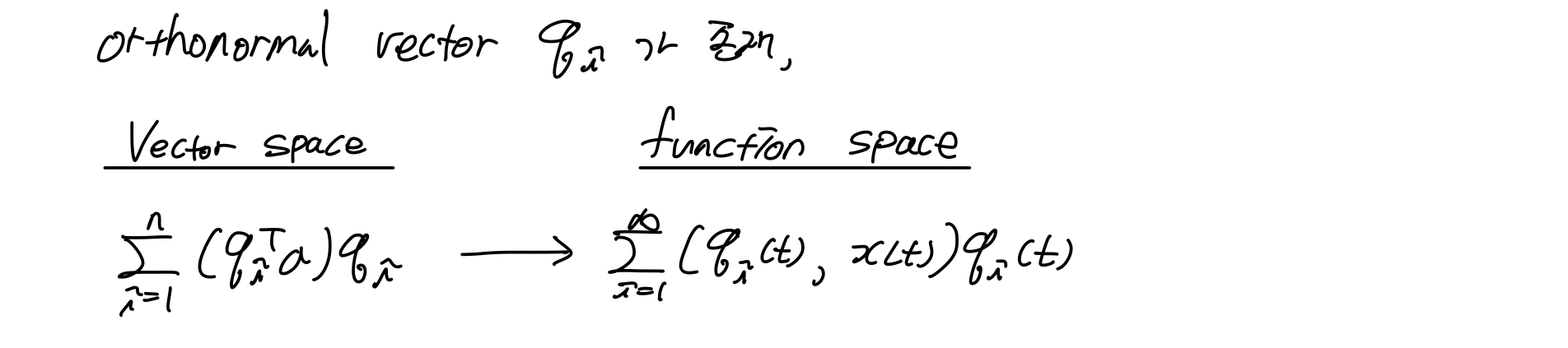
Hillber space는 함수를 벡터처럼 다루고 싶은 것이다. 이를 위해 함수의 각각 t라는 구간에서 t에 해당하는 값을 element로 쓰고, vector의 element 처럼 표현해주면 vector 개념을 function에서도 적용할 수 있다. Summation이 Integration으로 바뀌는 것뿐 나머지는 동일하다.
If given a basis, linear combination {} are unique!!
If given a basis function, series coefficients are unique!!
따라서 어떤 basis function에 따라 계수를 구하는게 쉽기도 어렵기도 하다. 그렇기 때문에 잘 정해야 하는데...
especially {cos(nt), sin(mt)} m, n are integer ()
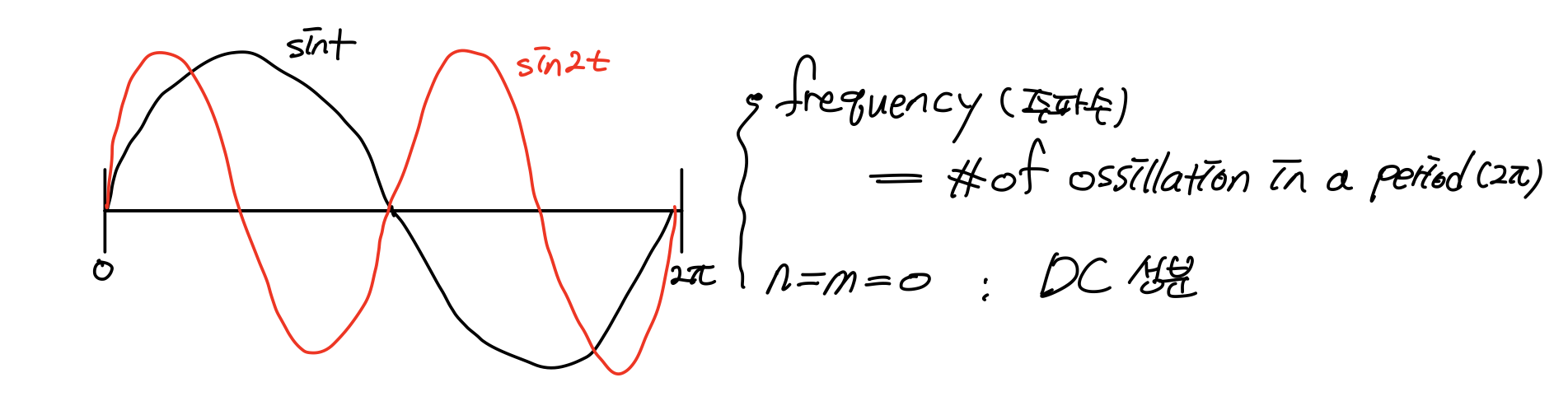
정리하면, basis func이 주어지면 어떤 형태로 라는 함수를 표현할 수 있다. 또한, basis와 의 coefficient가 주어지면 를 만들어 낼 수 있다. 이때 basis func을 를 주기로 갖는 {}로 잡아보자는 것이다.
중요한 건 n, m에 상관없이 cosnt와 sinnt는 서로 orthogonal 하다는 것이다. 이게 무슨 말일까? 알아보자!
Orthogonal basis functions

{} 조합은 서로 Orthogonal하다. 이것을 가지고 (0,2) 구간에서 함수를 해석해보겠다 하는 것이 Fourier Series이다.
Fourier Series
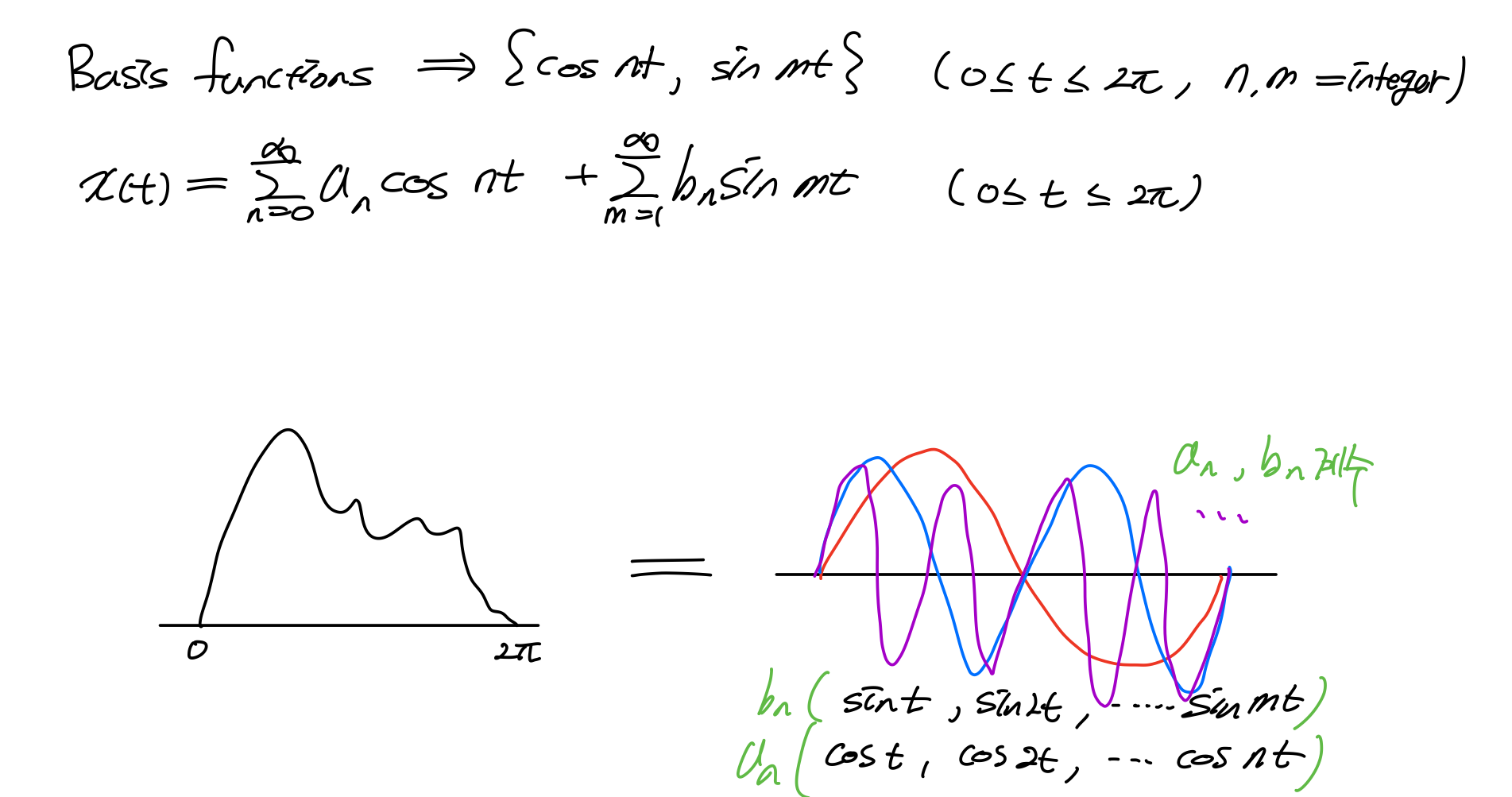
Fourier Series는 어떤 파형을 cos, sin의 조합으로 만들어주는 것이라 생각하면 쉽다. 그 값에 계수 을 곱해 어떤 파형도 만들 수 있다는 것!!!!
Gram-Schmidt for functions
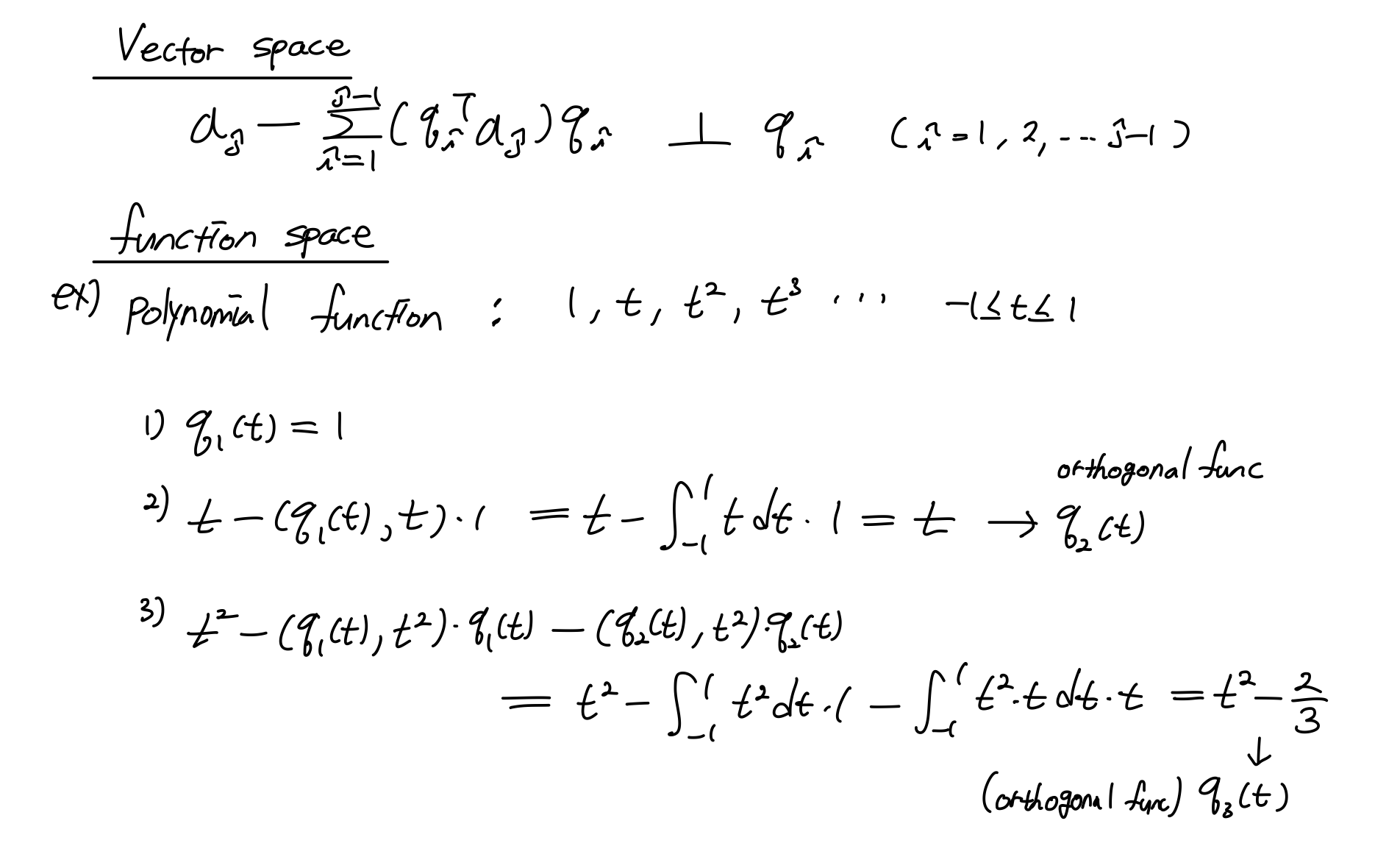
위의 방식을 반복하면 polynomial basis function이 서로 orthogonal function으로 만들어진다. 그리고 각 함수의 제곱으로 나누어주면 orthonormal basis function을 구할 수 있다.
