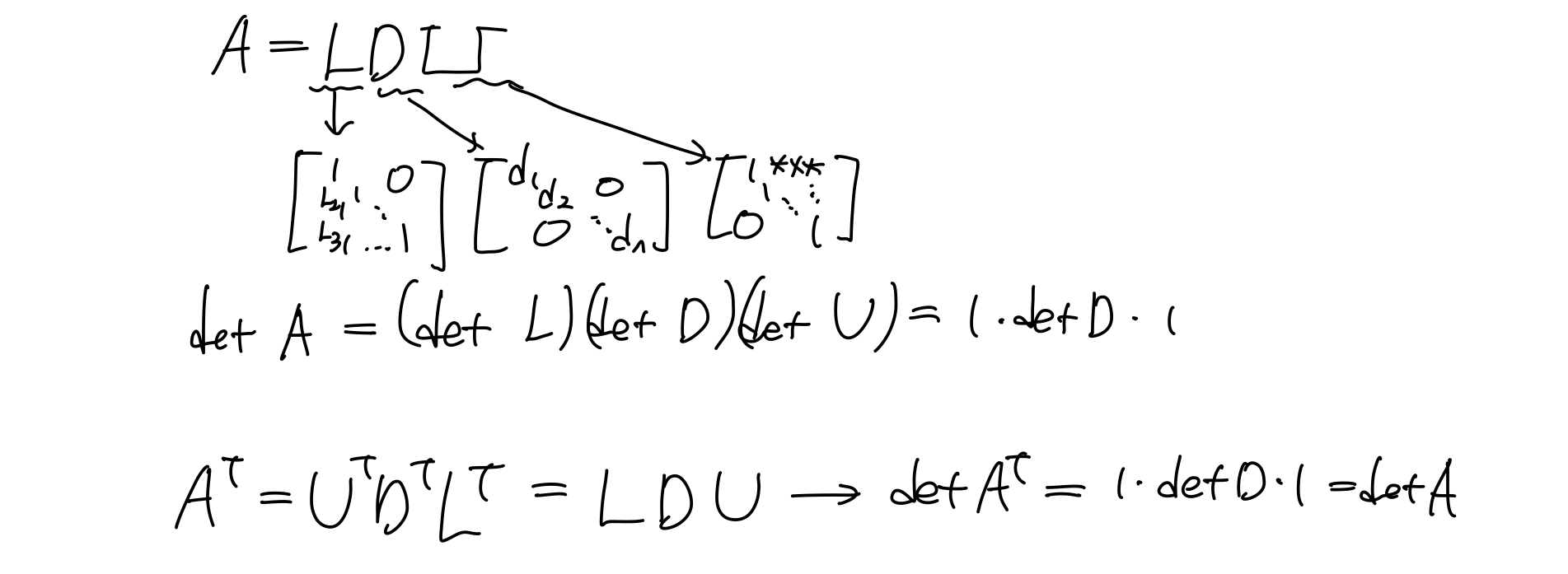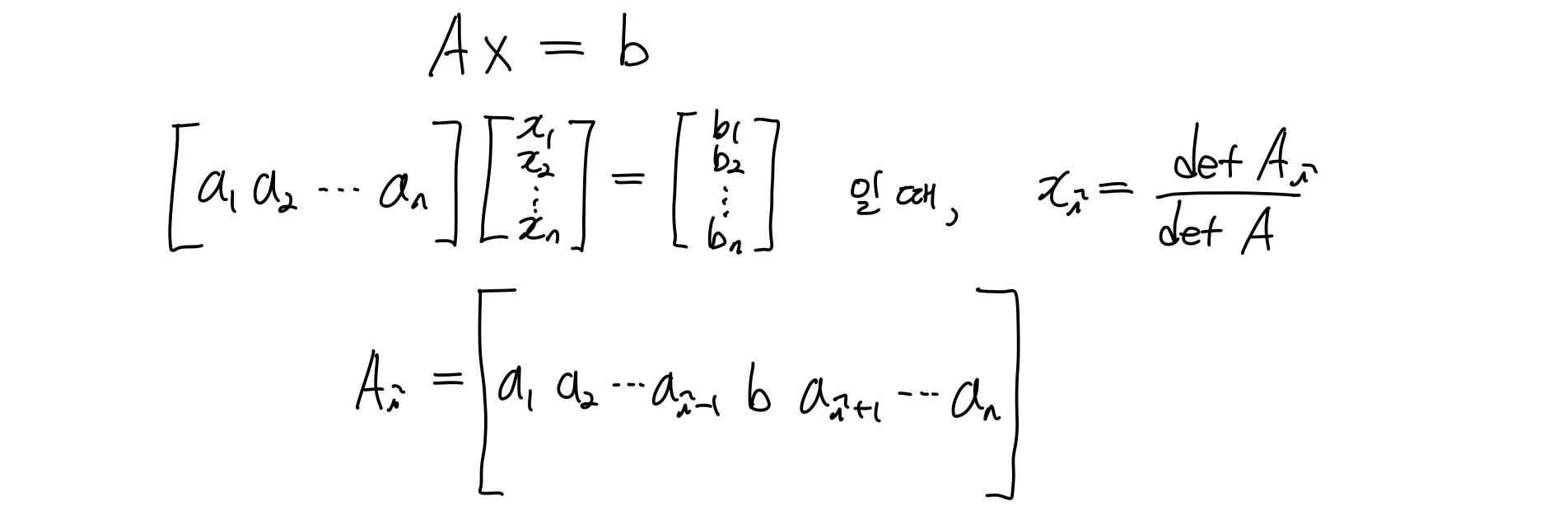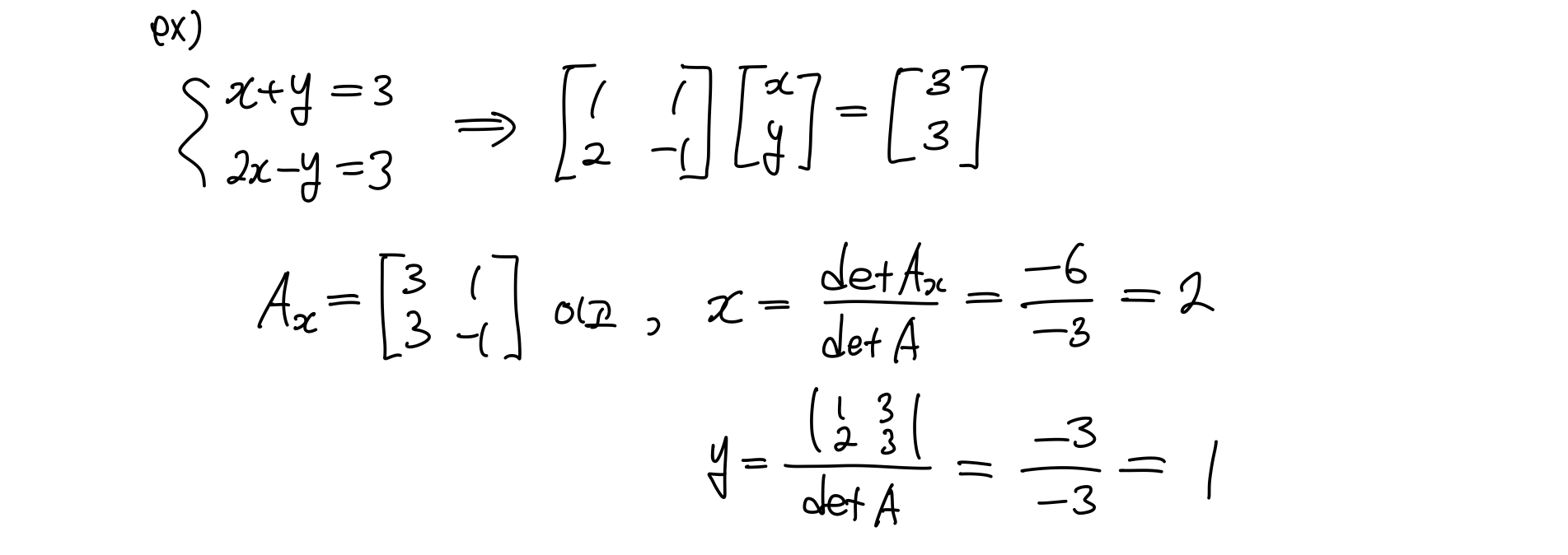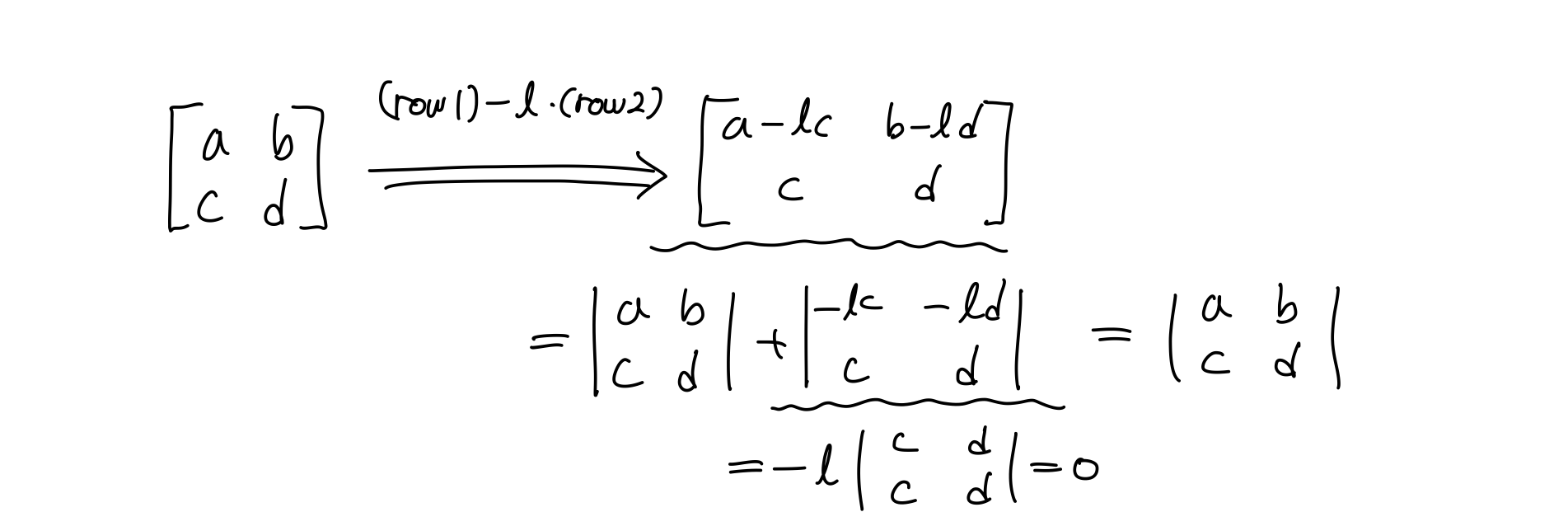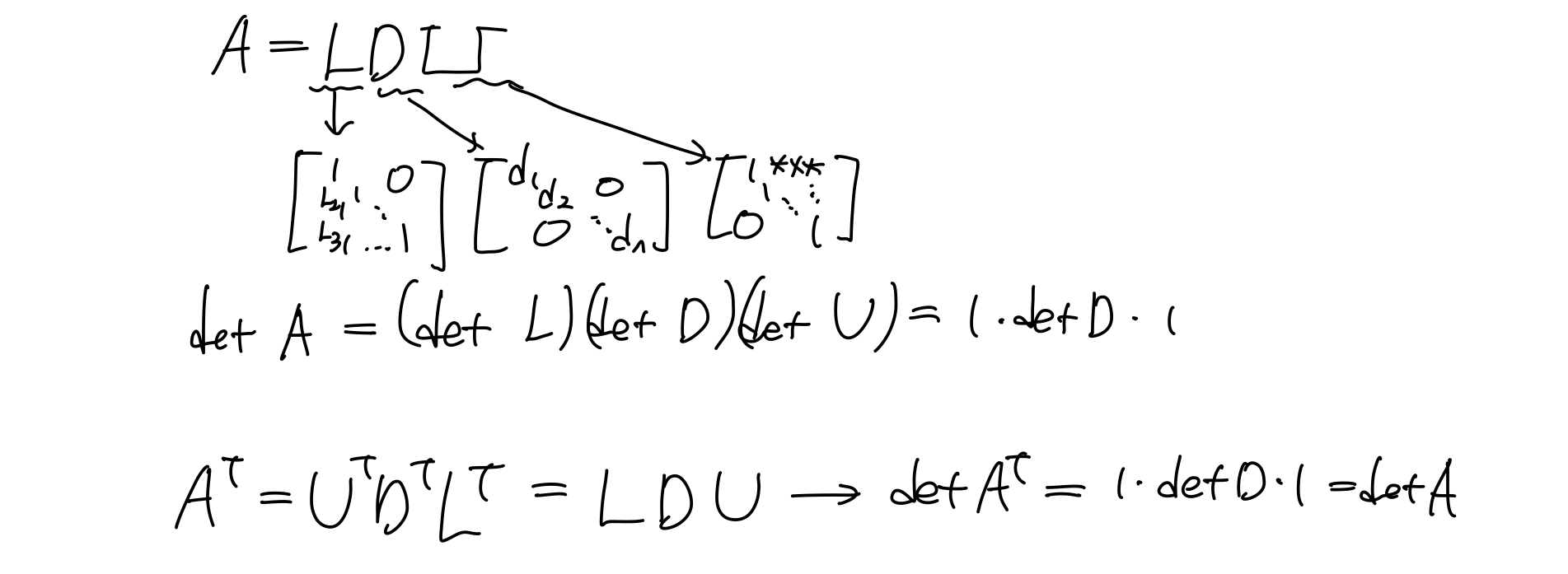"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.

for n x n square matrix det(A)
some properties of det(A)

square matrix의 determinent는 몇 가지 특징을 가지고 있다.

Square matrix' determinent properties

1) $A^{-1}$ exist, iff det(A) $\neq$ 0
2) det(A) equal volume of a box in $R^n$

두 번째 특징의 경우는 determinent가 n차원의 공간을 나타낼 수 있다는 말로 Jacobian을 말한다.

Jacobian

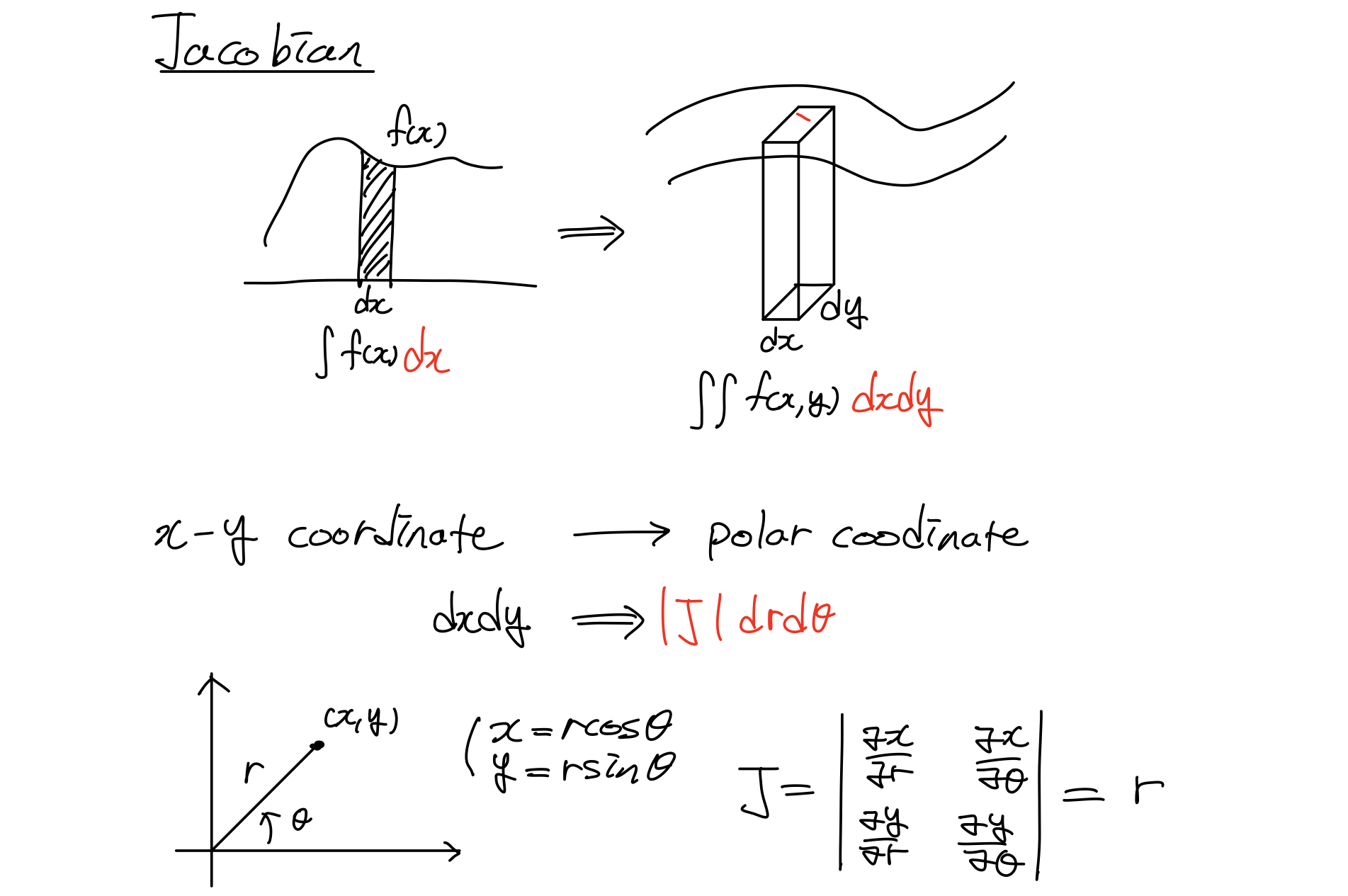
Jacobian은 coordinate 변환행렬이다. 위의 사진에서 x라는 변수 하나를 가지고 있을 때는 하나의 변수로 하나의 변수로 치환, 즉 길이를 길이로 치환하기 때문에 쉽다. 하지만 변수가 x, y 2개로 늘어나면 다른 변수(ex. polar coodination)로 치환할 때, 치환하고자 하는 변수의 면적 $dxdy$가 치환하고자 하는 변수의 면적 $drd\theta$으로 1대1 대응으로 변하지 않는다. 하나의 factor가 붙는데 그것이 변환행렬이라 부를 수 있는 Jacobian이다.

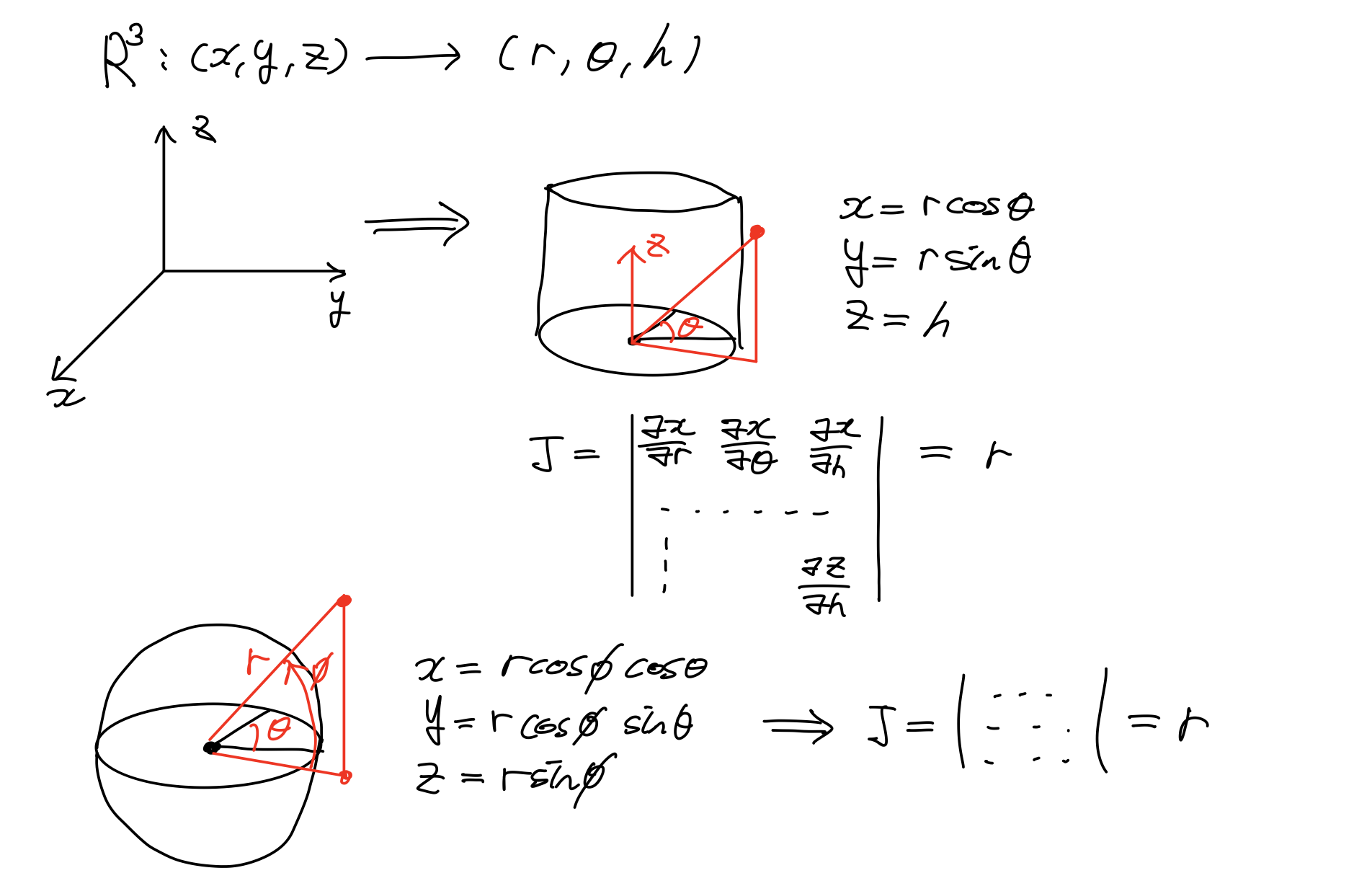
대표적인 coordinate로 3차원 좌표를 원기둥좌표, 구좌표 변환하는 것이 있다.

3) det(A) = $\pm$(product of pivots)

(오랜만에 듣는) Gauss Elimination에서 우리는 0이 아닌 pivot의 곱이 determinent가 된다는 사실을 알았다. 근데 왜 $\pm$부호가 붙나?? 소거하는 과정에서 pivot이 0이 될 때 행렬의 행을 바꿔주는 pivoting을 해주었는데, 이때 determinent의 부호가 바뀐다. 때문에 부호가 붙는다.

4) Cramer's Rule

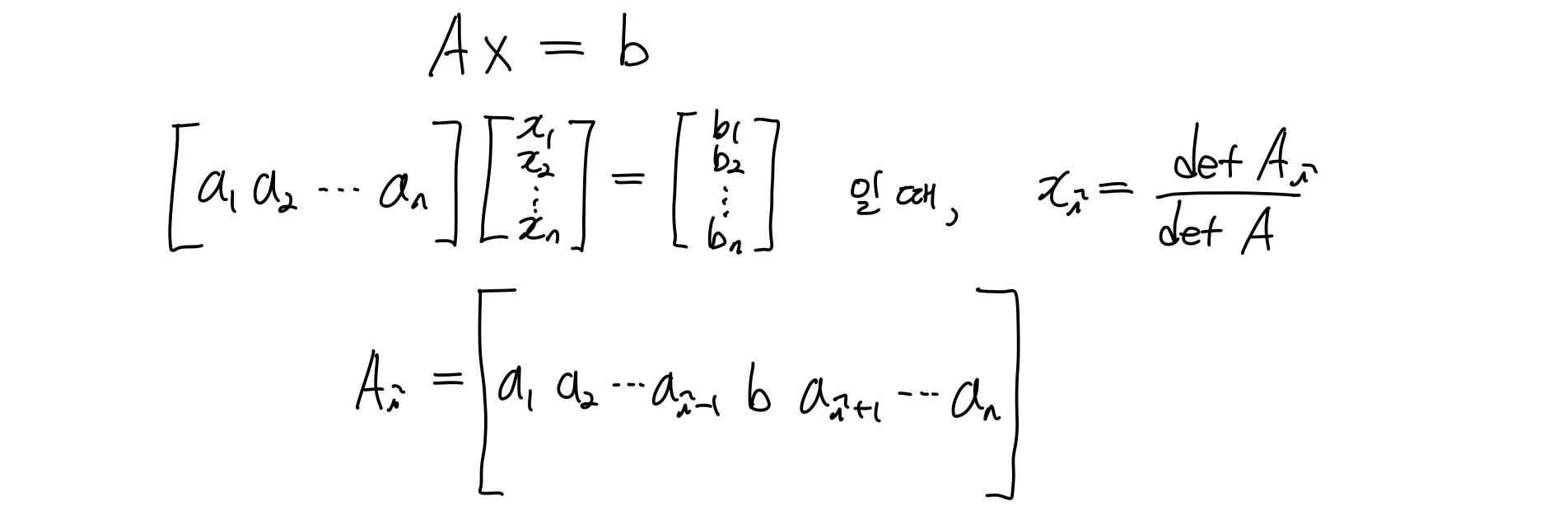
1차 연립방정식을 풀 때, 해를 구하기 위해 별 짓을 다 했었는데...Cramer' rule은 determinent를 이용해 쉽게 해를 구하는 방법이다. 예를 보자.

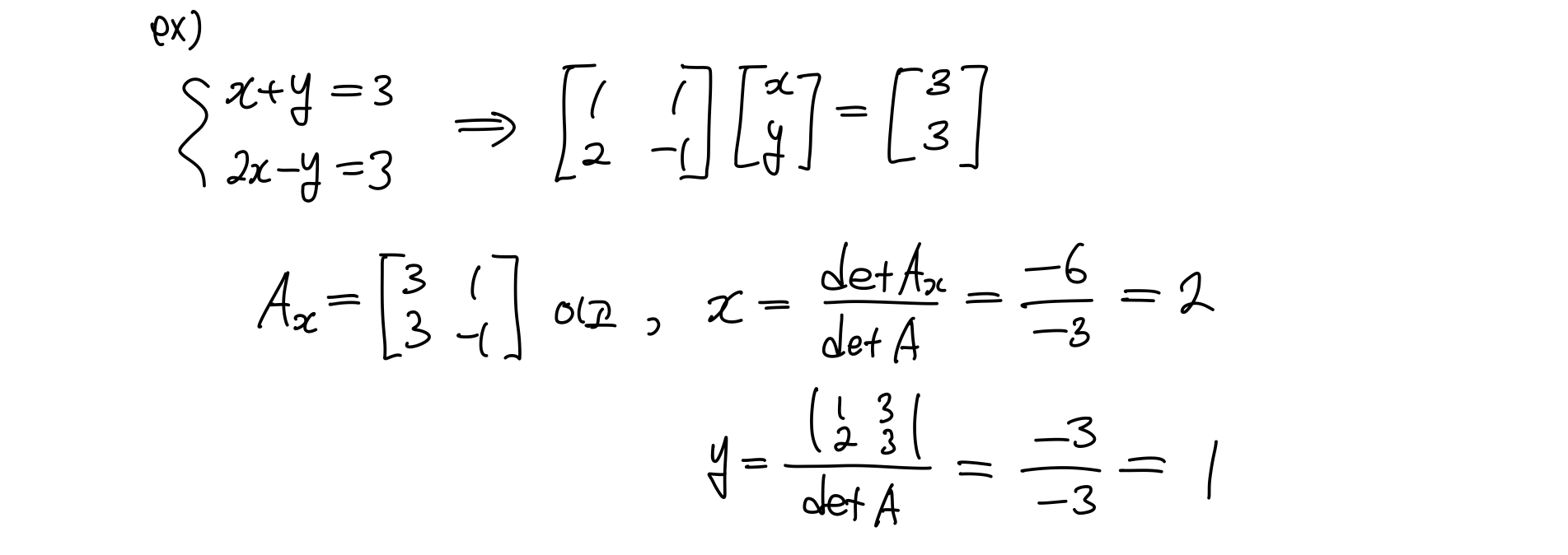
Properties of Determinents

Consider 2x2 matrix to make sure some basic properties, expand to turn nxn matrix

3 basic properties

1) det( I ) = 1
2) det( A ) changes the sign when two rows are interchanged

두 번째 특징은 G.E에서 pivoting을 할 때마다 determinent의 부호가 바뀐다는 소리다. 즉 1행과 2행을 바꿔주면 부호가 바뀌고, 다시 2행과 3행을 바꿔주면 다시 부호가 바뀌어서 원래 부호로 돌아오게 된다는 소리!!

3) det( A ) depands linearly on the first row

determinent에서 첫 번째 행은 선형성을 갖는다. 주의!! 오직 첫 번째 행만 선형성을 갖는다!! 선형성 linearity란, Homogenity하고 Superposition의 특징을 모두 갖을 때를 말한다.

각 determinent를 구하면,

가 된다. 이 특징을 이용하면 여러 형태의 determinent의 형태를 이용할 수 있다.

그리고 선형성의 특징 Homogenity를 다루면,

이는

따라서

가 된다.

additional properties by 3-basic properties

4) If two rows ar equal, det(A) = 0

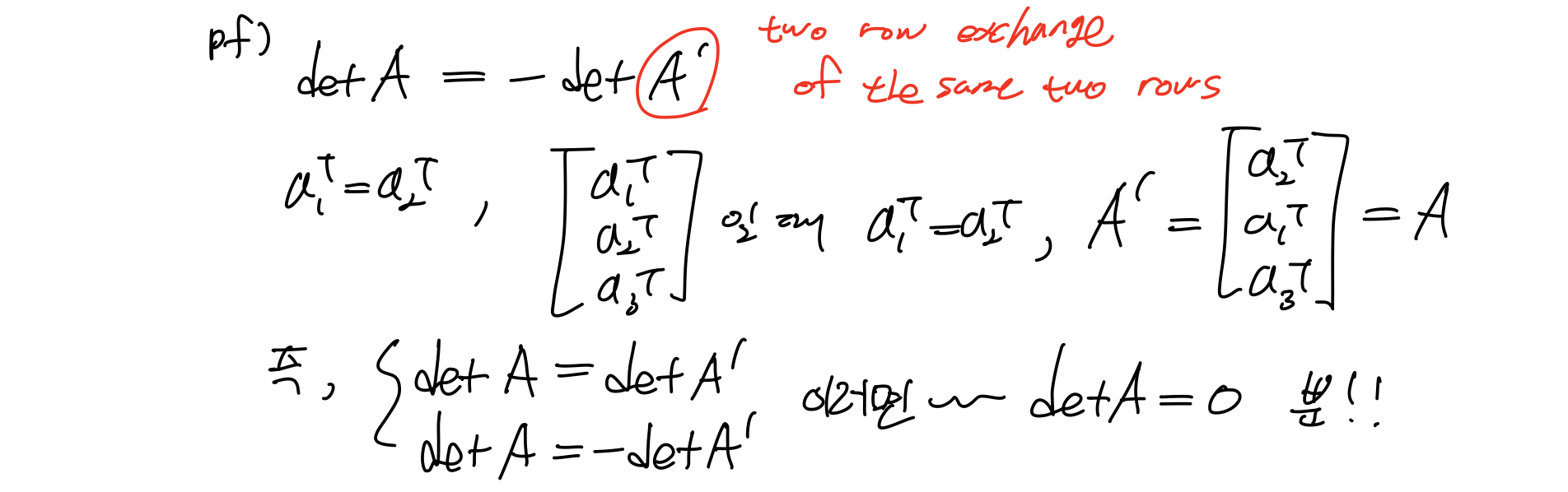
A'이 행렬A의 같은 두 행을 바꾼 행렬이라 할 때, 위의 특징이 성립한다. 결국 A=A'이기 때문에 det(A)=det(A')이면서, basic property에 의한 det(A)=-det(A')도 만족하기 위해서는 det(A)=0이어야만 한다.

5) Row operations do not change the determinent

In G.E, substracting a multiple of one row from another row. 우리는 G.E에서 행을 소거하기 위해 곱하고 빼주었떤,

예를 들면,

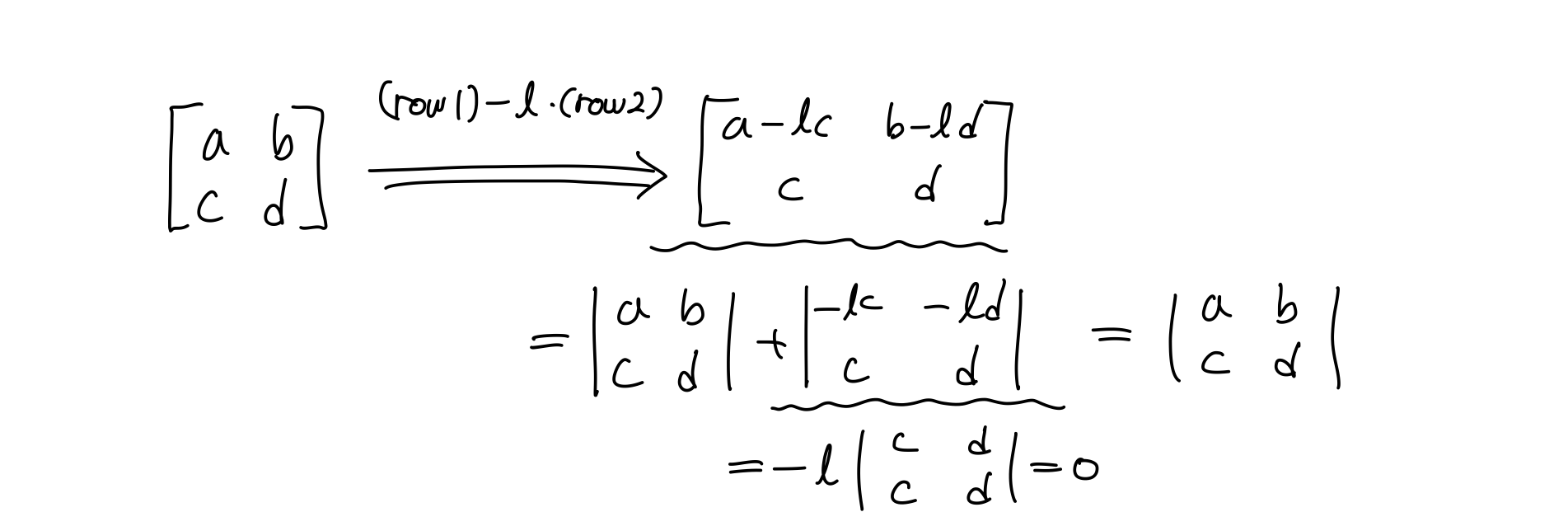
6) If A has a zero-row, det(A)=0

0인 행ㅇ이 존재할 때 determinent는 0이 된다. 당연!!!

7) If A is triangular, det(A)=product of diangonal entries

8) A: singular(특이), det(A)=0 $\rightarrow A^{-1}$ not exist
non-singular, det(A) $\neq 0 \rightarrow A^{-1}$ exist

9) det(AB) = det(A) + det(B)

10) det($A^T$)=det(A)