"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.

Eigenvalue & Eigenvector

처음부터 지금까지 우리는 $Ax=b$ 연립방정식의 해를 구하기 위한 여러 방법(?)을 배웠다. $b = 0\ or\ b\neq 0$, 방정식 수와 미지수 수의 관계에 따라 해를 유일해 혹은 무한해는 Vector Space 라는 개념을 가져와 해를 표현했다. 그리고 이제 새로운 방식을 또 하나 배웠는데, 그것이 바로 Eigenvalue, Eigenvector!!!

$Ax=b$로 표현하기 지겨워~ 그래서 이번에는 $Ax$를 scalar multiplication 으로 표현하려 하는 짓이!! 바로 eigen!!

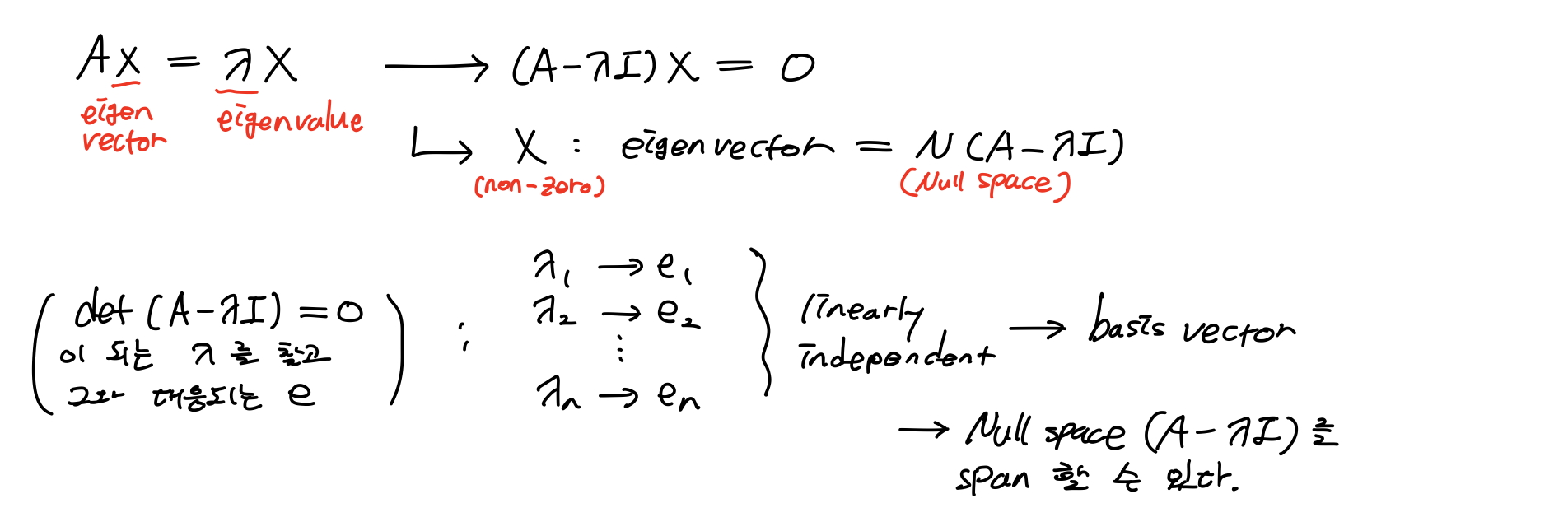
Property

Eigenvalue의 특성은 다음과 같다.

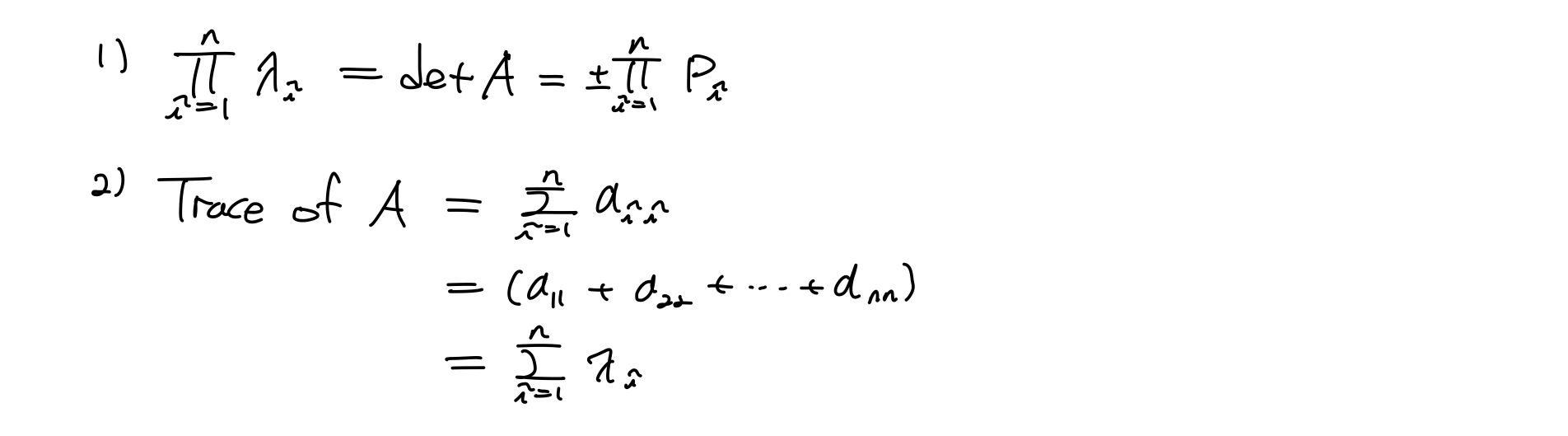
먼저 두 번째 특징에 대해서 증명하면,

그리고 첫 번째 특징에 대해서 증명하면,

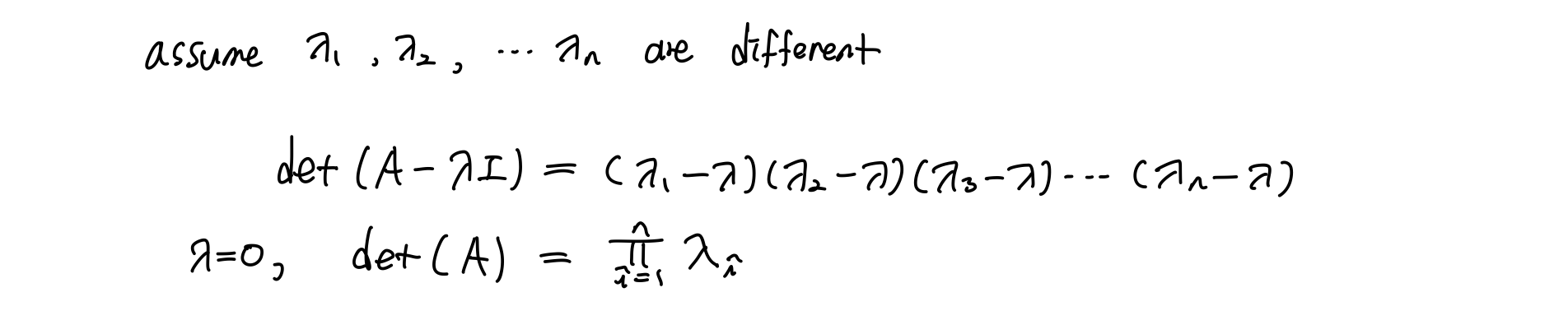
Digonalization

앞에서 행렬A를 factorization하는 방법 두 가지(LDU, QR)에 대해 배웠다. 그리고 새롭게 배운 eigenvalue, eigenvector를 이용해 행렬A를 factorization하는 방법에 대해 배웠다.

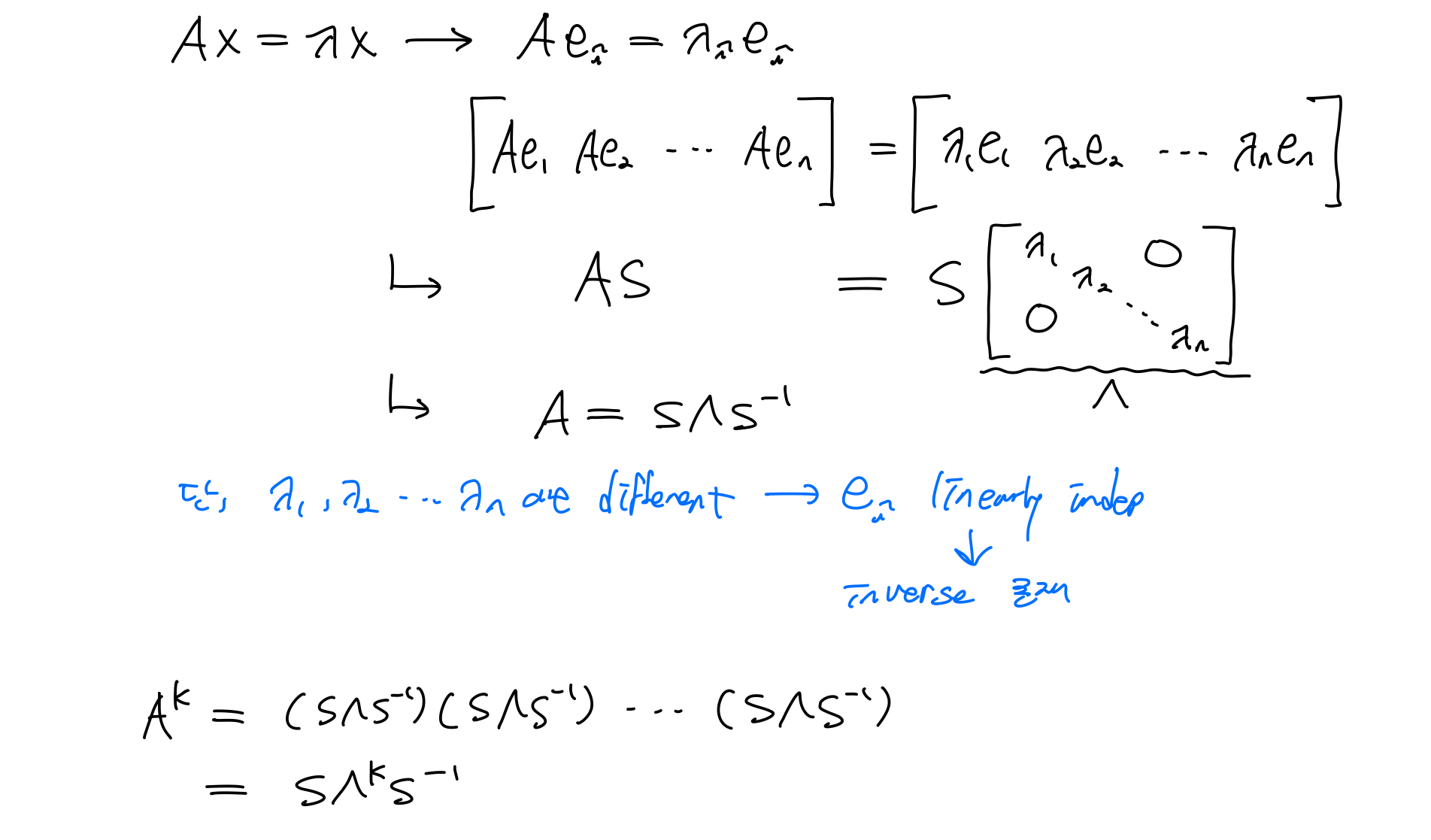
Difference eqn & $A^k$

이번에는 고등학교 때 배운 수열을 eigenvalue와 eigenvector를 이용해 풀어보려 한다. 세상에 많은 자연적현상은 수열의 조합으로 표현할 수 있다고 한다.

마치 우리가 $Ax=b$에서 A를 system이라고 생각하고 해결하는 것과 같이, system eqn을 $u_{k+1}=Au_{k}$로 만들면 eigenvalue decomposition으로 풀 수 있다.

Least Square