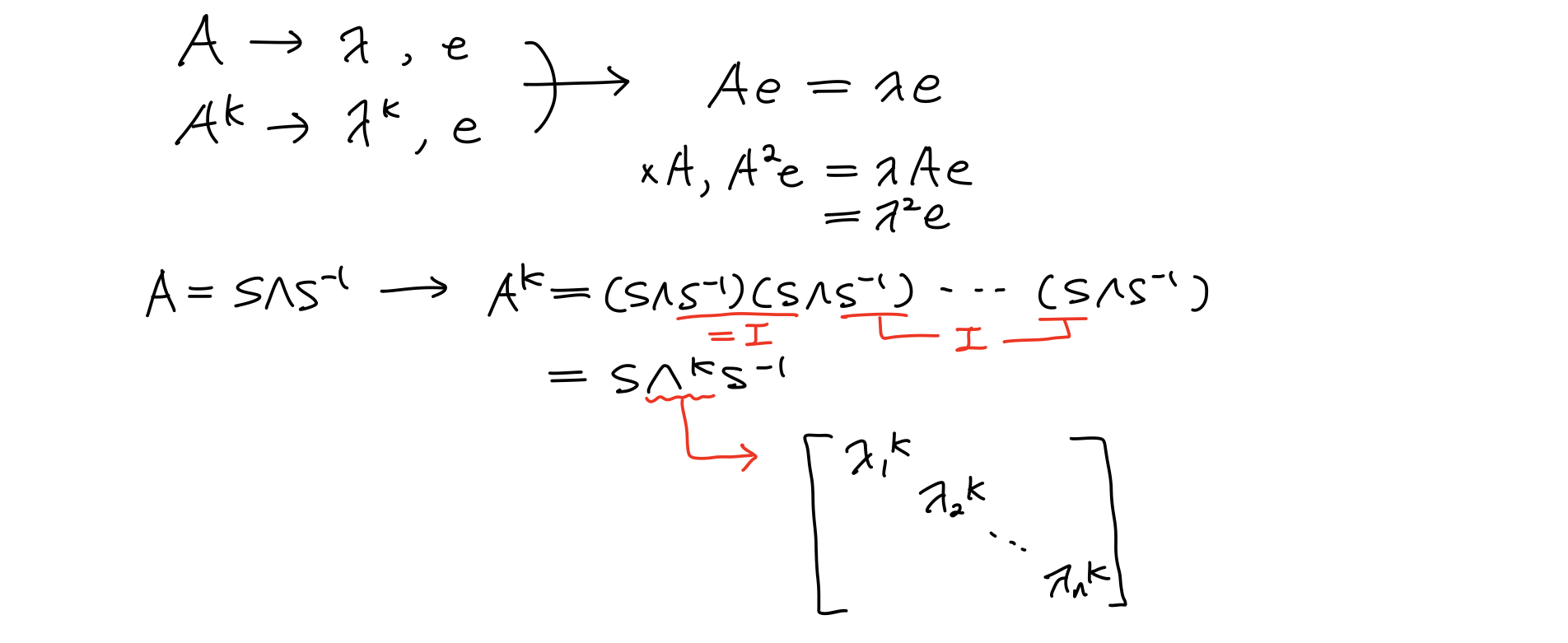"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.

Eigenvalues and Eigenvectors

우리는 Ax=b 연립방정식의 해를 구하는 방법에 대해 지금까지 알아보았는데요. 이때 A를 system 관점으로 보면, x는 input이고 b는 output, A는 두 입출력의 관계를 나타내는 system이다. 이 A를 factorization하여 더 쉽게 표현할 수 있다면 입출력의 관계를 더 쉽게 표현할 수 있지 않을까?

고유값과 고유벡터는 이 질문에 대한 답이 되는 개념이라 할 수 있어요.

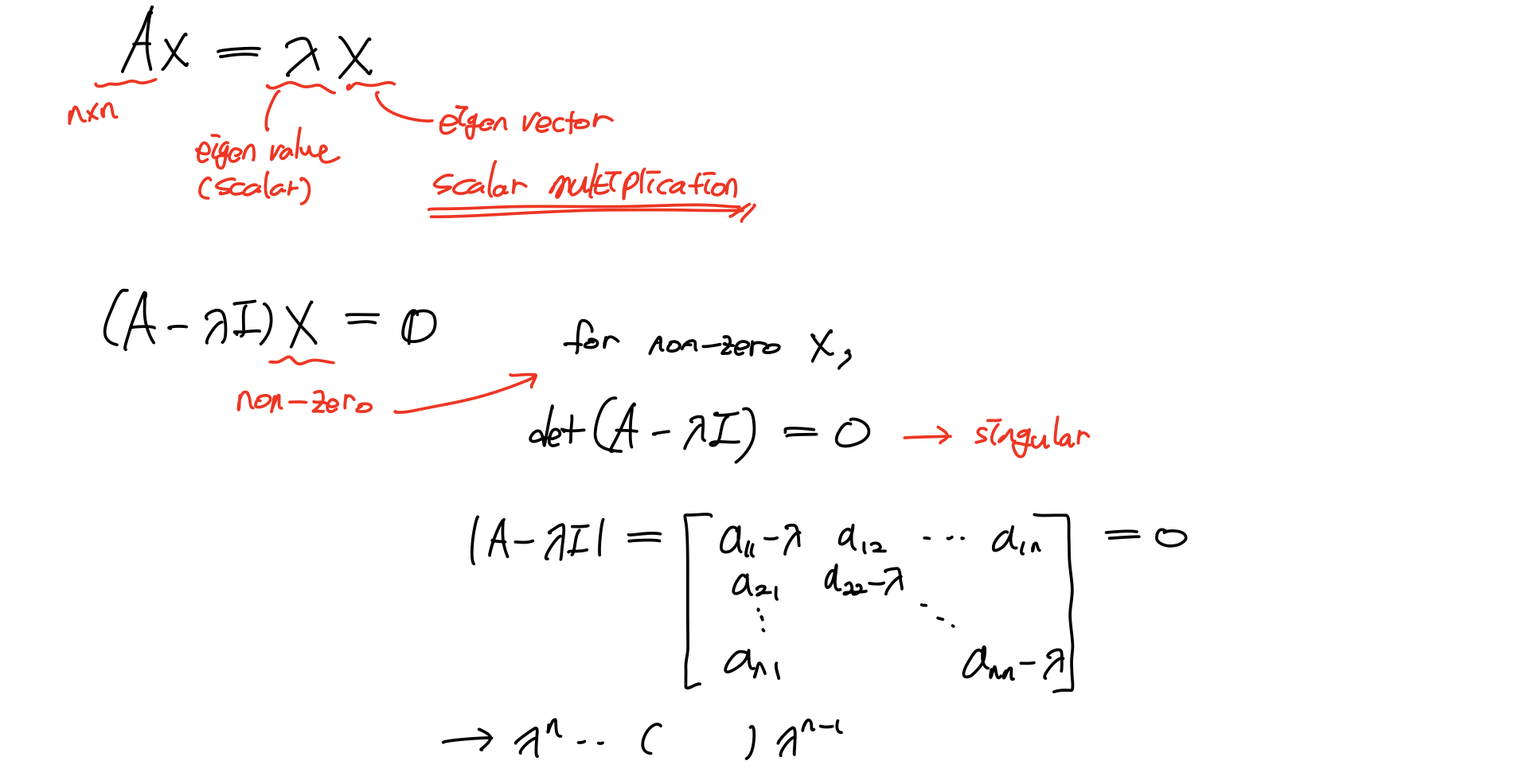
Ax는 multiplication of matrics인데, 이것을 scalar multiplication 으로 표현하는 것입니다. eigenvalue는 $det(A-\lambda I)=0$일 때 $\lambda$ 입니다.

그렇다면 eigenvector는 뭘까요? 예시를 통해 알아보죠.

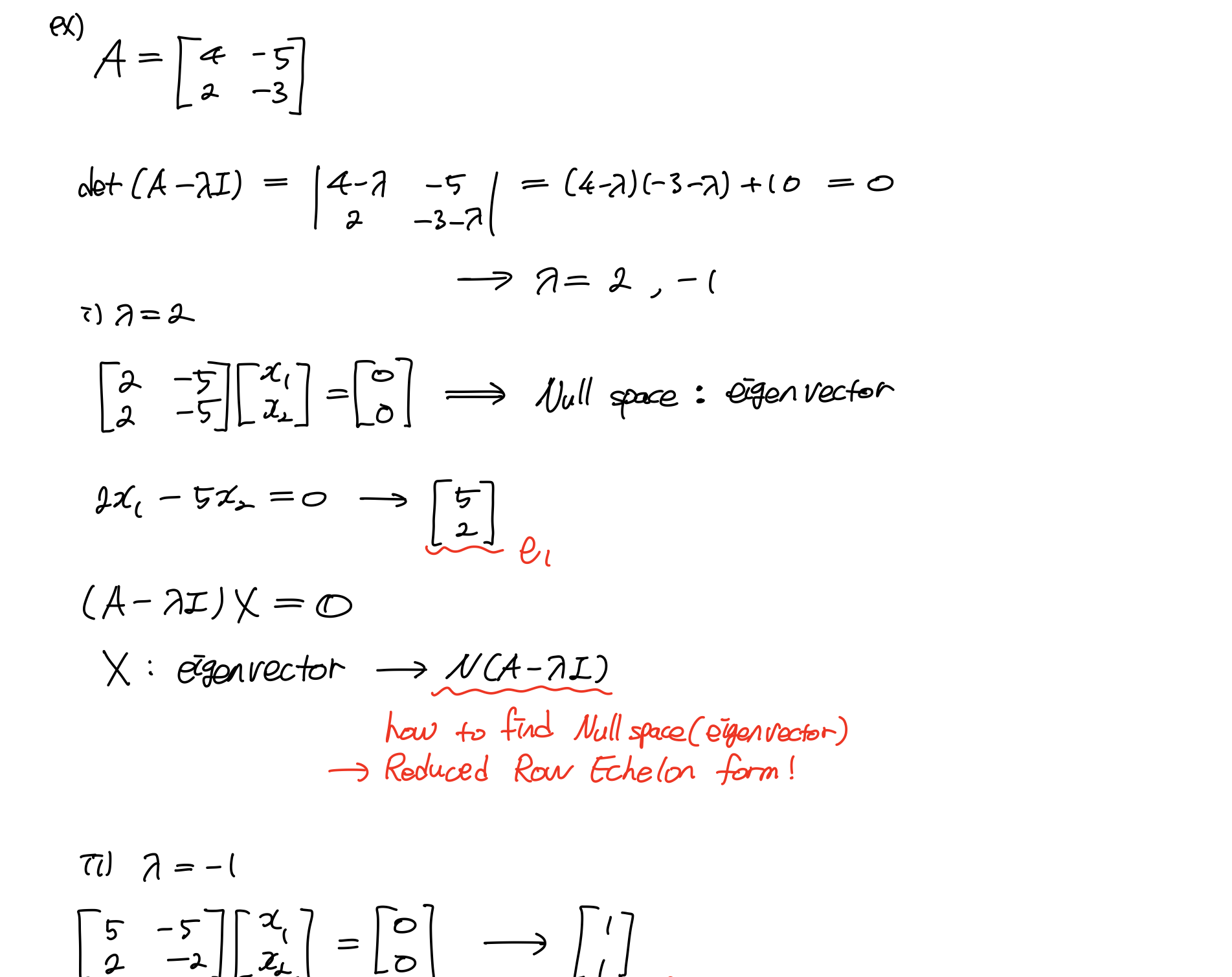
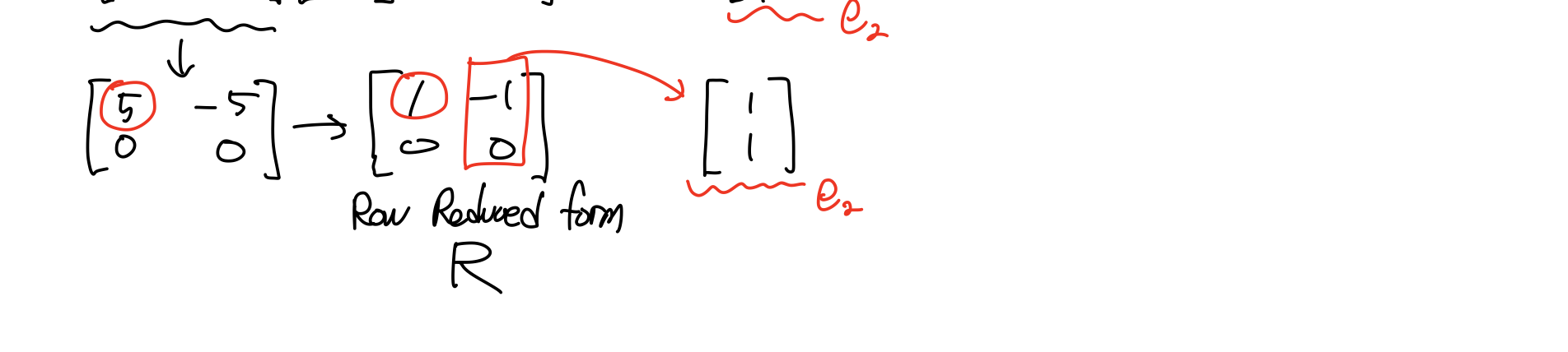
eigenvector는 구한 eigenvalue에 대응되는 vector 인것을 알 수 있습니다. 또한 $(A-\lambda I)X=0$의 해이기도 합니다. 근데 어디서 많이 본 모양이쥬? 앞에서 배웠던 $AX=0$의 해의 집합 Null space가 eigenvector이라는 것을!!!

그리고 Null space(eigenvector)를 구하는 방법도 알고 있쥬? Reduced Row Echelon form R을 구해 special sol 과 particular sol을 구하는 것이쥬~

Diagonalization of matrix

앞에서 행렬A를 factorization하는 방법 2가지를 배웠어요.

첫 번째는 LU decomposition

두 번째는 QR decomposition

그리고 새로운 factorization을 알아볼 것 입니다!!
그것은 바로~ $S\Lambda S^{-1}$ decomposition

증명해보자!!

$\rightarrow AS=S\Lambda \rightarrow A=S\Lambda S^{-1}$

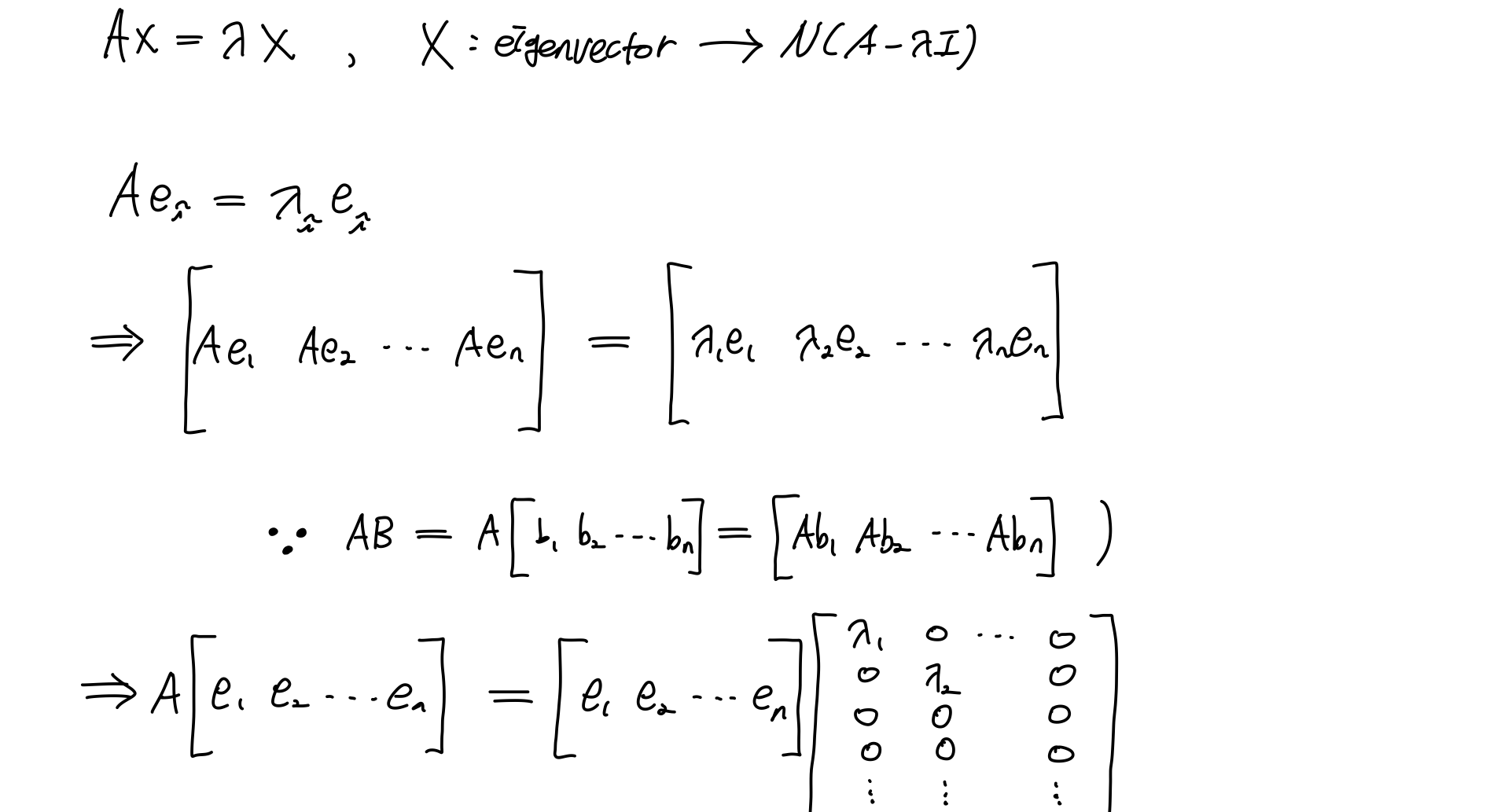
예를 들어보자!!

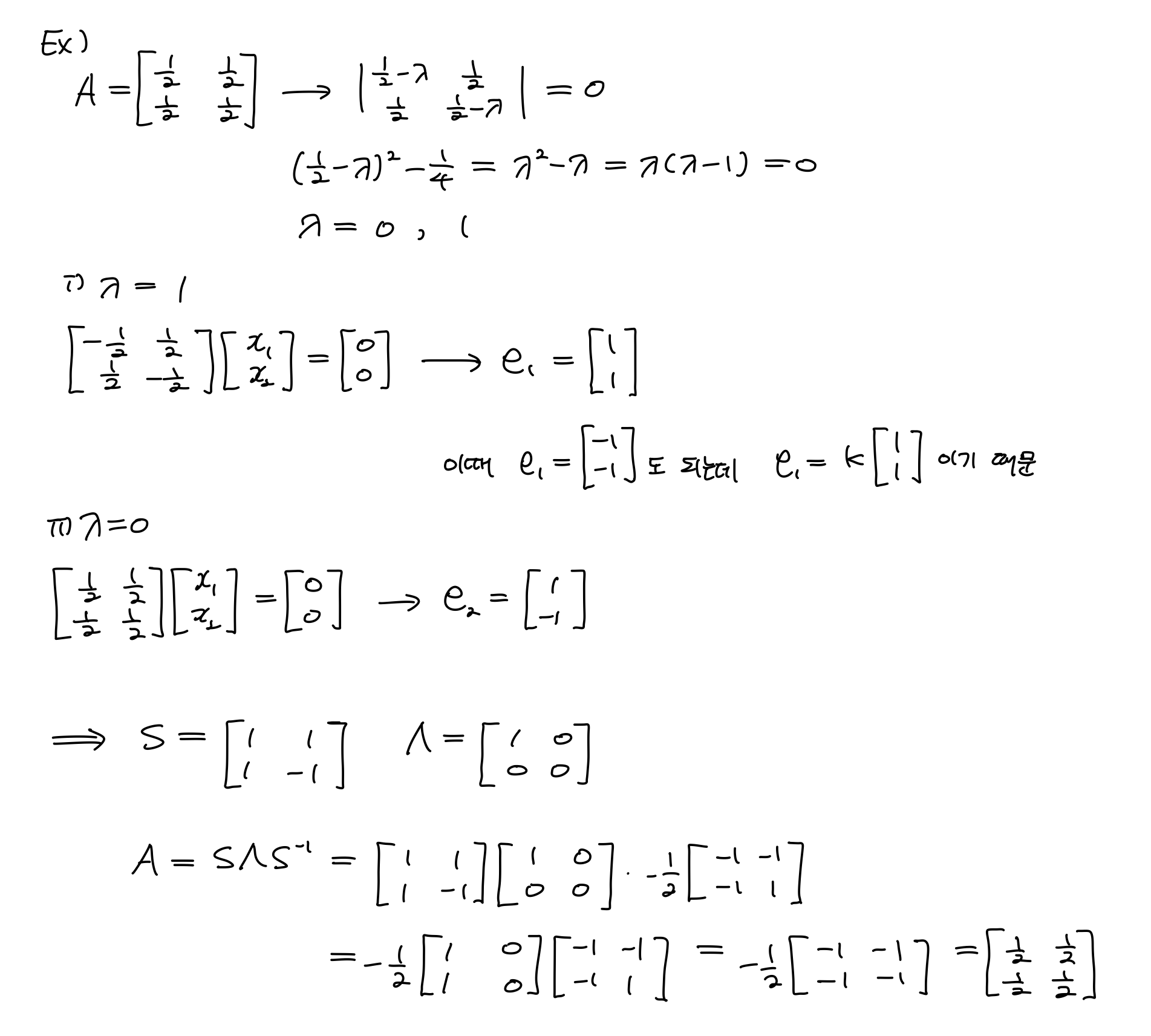
자, eigenvalue는 Ax를 scalar multiplication으로 표현해준다고 했다. 그렇다면 모든 실수, real number만 해당될까? 복소수 complex number는 안될까?

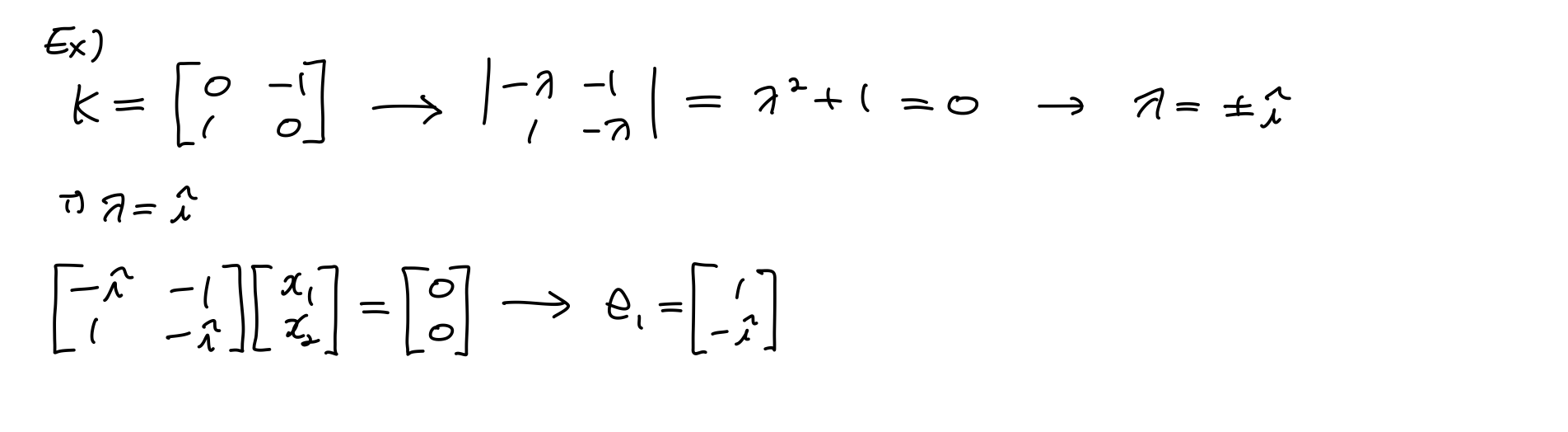
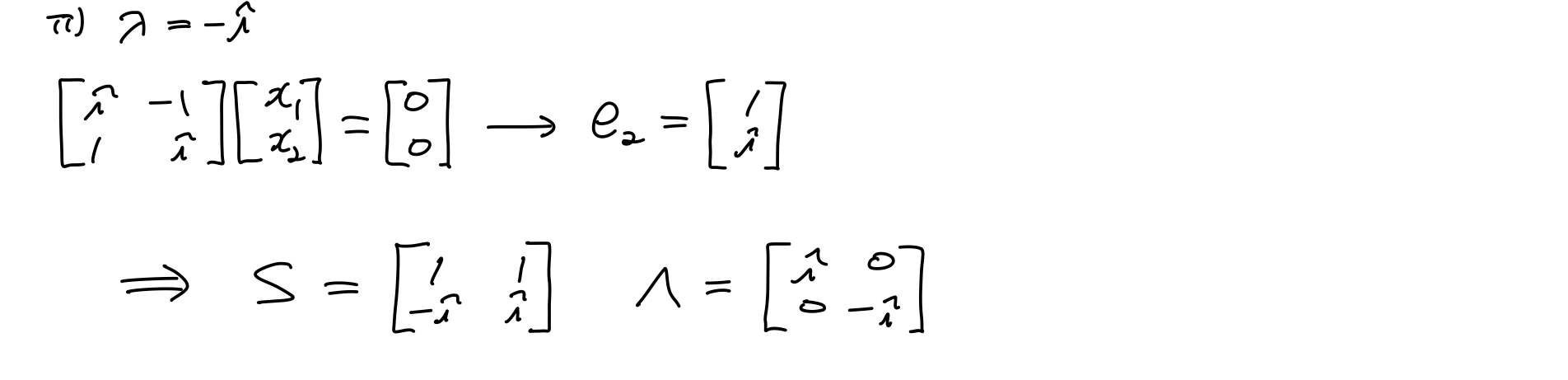
eigenvalue는 실수, 복소수에 상관없이 갖을 수 있다는 것을 알 수 있다.

이제 eigenvalue와 eigenvector의 특성에 대해 알아보자.

Property

1. If $\lambda_1,\lambda_2, ... \lambda_n$ are differents, then $e_1, e_2, ... e_n$ are linearly independent

2. S is not unique, since $ke \rightarrow eigenvector$

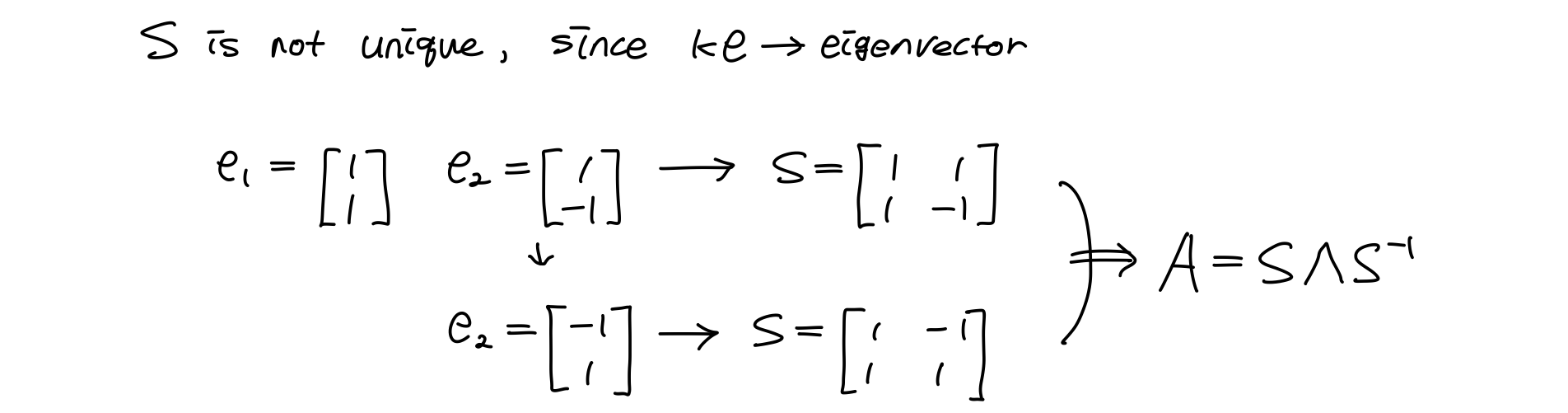
3. The order of eigenvalues is same with that of eigenvectors

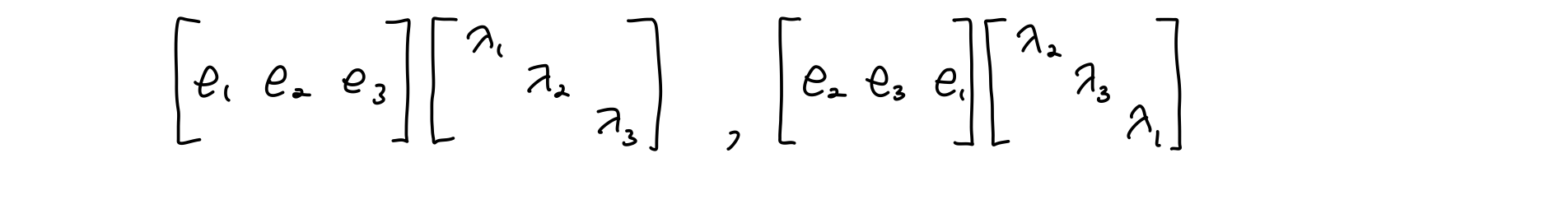
4. Not all matrices have n linearly independent eigenvectors

5. Powers