"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 확률과통계 수업을 정리한 내용입니다.

Review last lecture

Discrete인 경우에 할 수 있는 것은 X라는 RV이 특정한 Real number x에 대응할 때 x에 index를 붙일 수 있다는 것이다. 즉, descrete하니까 하나하나의 값이 어떠한 형태로든 우리가 그 값을 찾을 수 있다는 말이다. discrete한 x_i 값은 유한할 수도, 무한할 수도 있지만! 셀 수 있다는 점이 특징이다.

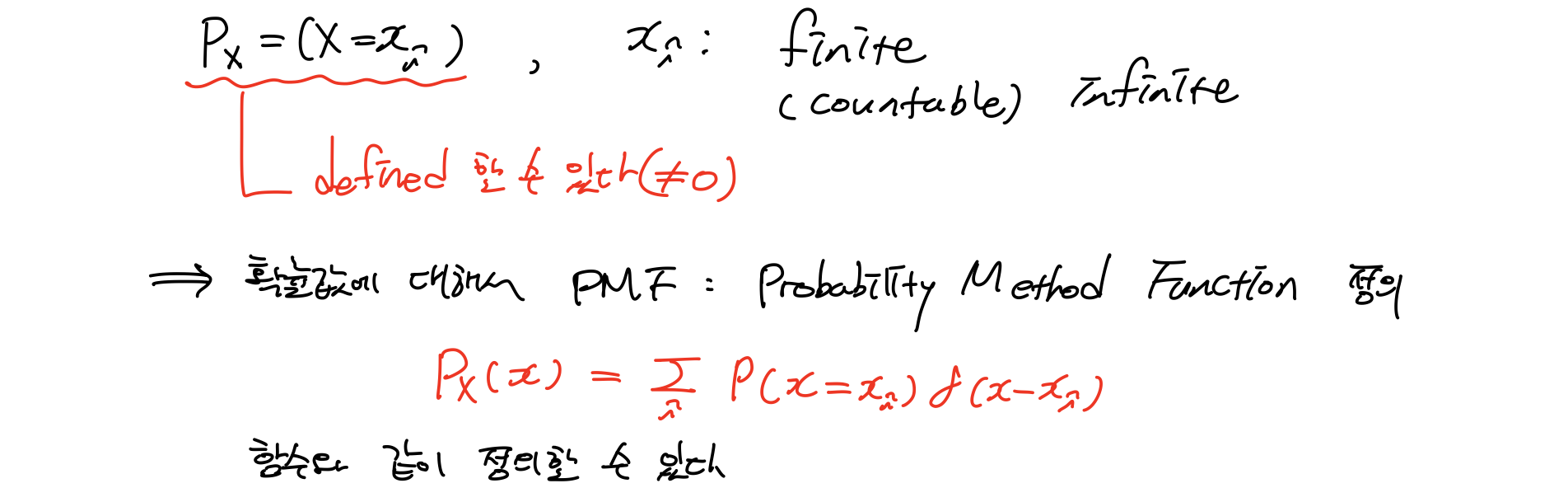
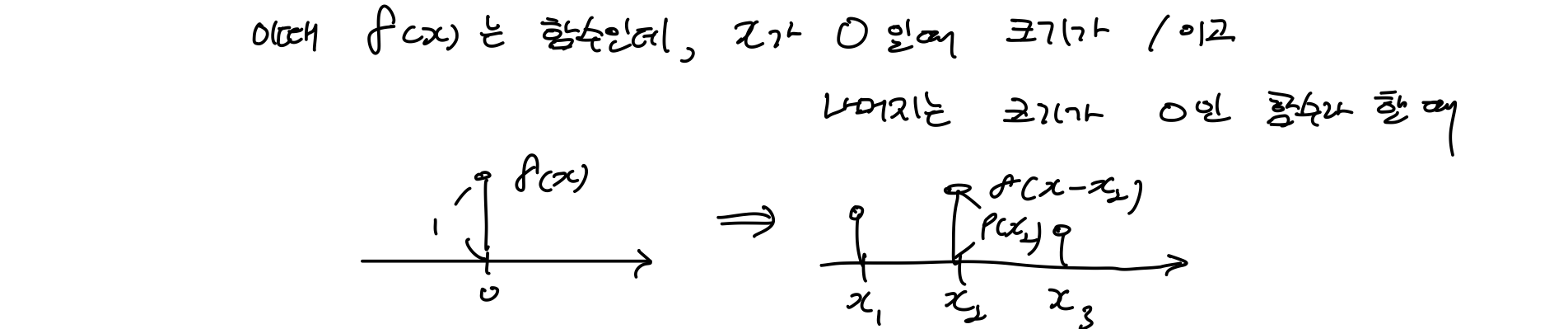
그렇다면 Descrete 경우의 CDF(Cumulative Distribution Function)은 어떻게 될까?

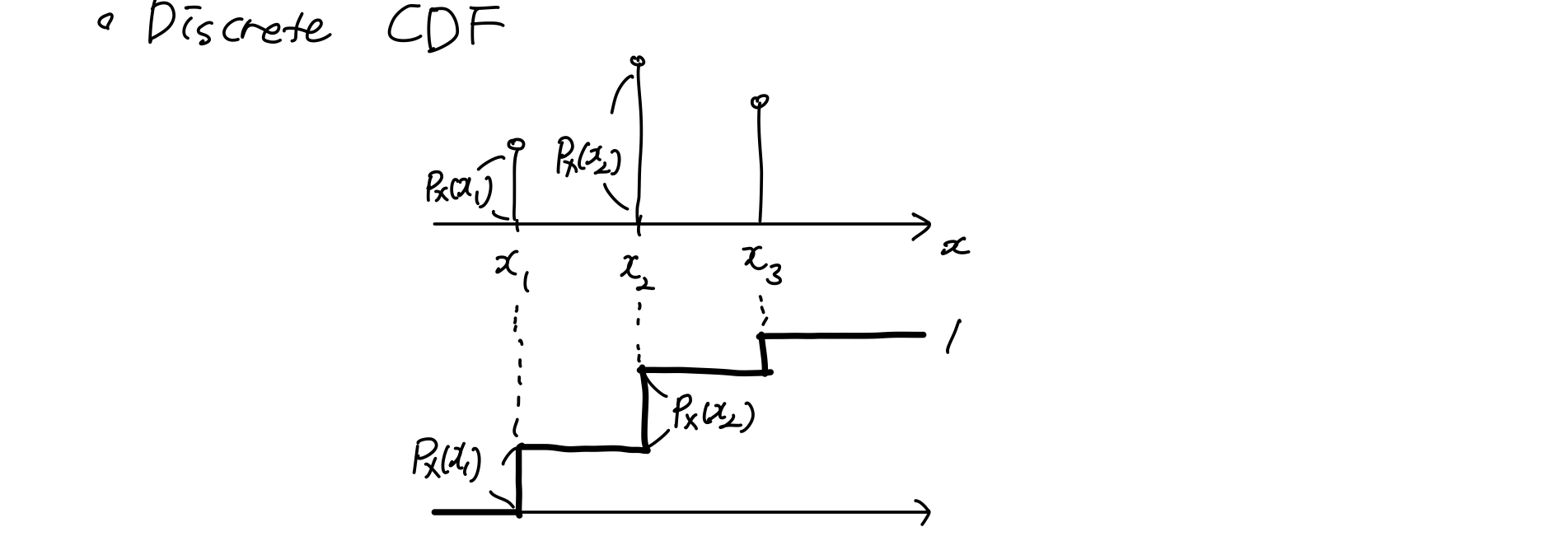
위의 사진과 같이 계단형 CDF 형태로 나타나는 것을 알 수 있다.

Continuous RV

이번에는 어떤 outcome을 모든 Real number에 대응시키는 Continuous RV에 알아보자.

Sample space S와 모든 실수 R에 대응시켜 나오는 확률변수를 continuous라고 하면, S 역시 무한히 많아야 대응이 가능하다. 따라서 S와 R 모두 셀 수 없을(uncomtably infinite) 많아야 한다.

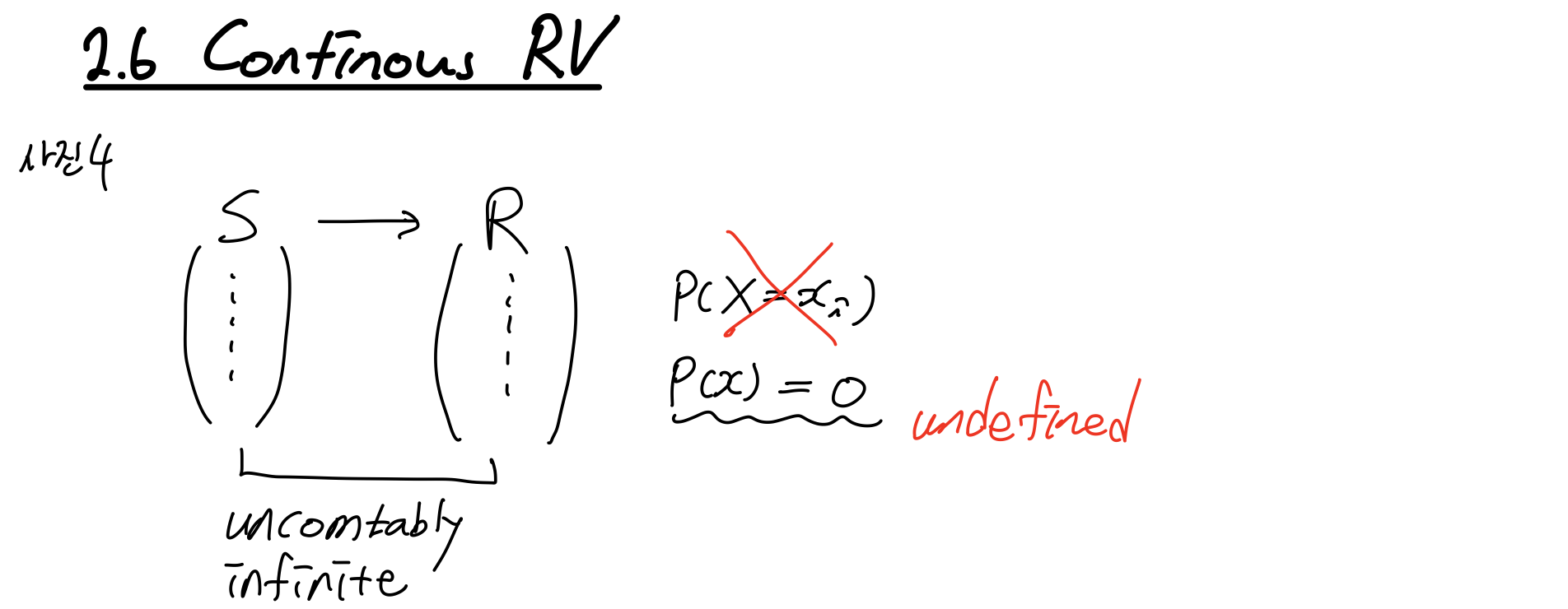
그러면 0과 1 사이에 어떤 실수(0.50000...)를 뽑는다고 하자. 이것이 발생할 가능성은 얼마일까? 셀 수 없이 많은 실수들 중 0.5를 뽑을 확률은 0에 가깝다. 따라서 확률 자체를 define하는 것이 Continuous RV에서는 어렵다는 것을 알 수 있다. Discrete RV와 달리 새롭게 Continuous RV의 확률분포에 대한 함수를 정의할 필요가 있다. 이때 CDF를 활용한다.

For continuous RVs,
P(x) --> 0
it is not possible to define a probability value for each x

위 식의 물리적인 의미를 생각해보자. 분자는 확률, 분모는 x축의 짧은 길이. 즉, 확률값이 길이당 얼마이다. 따라서 Probability density function(pdf)로 정의한다. 이로써 Countinuous RV의 확률분포를 정의해볼 수 있다. 아래는 continuous RV의 성질과 예제이다.

property and example of continuous RV

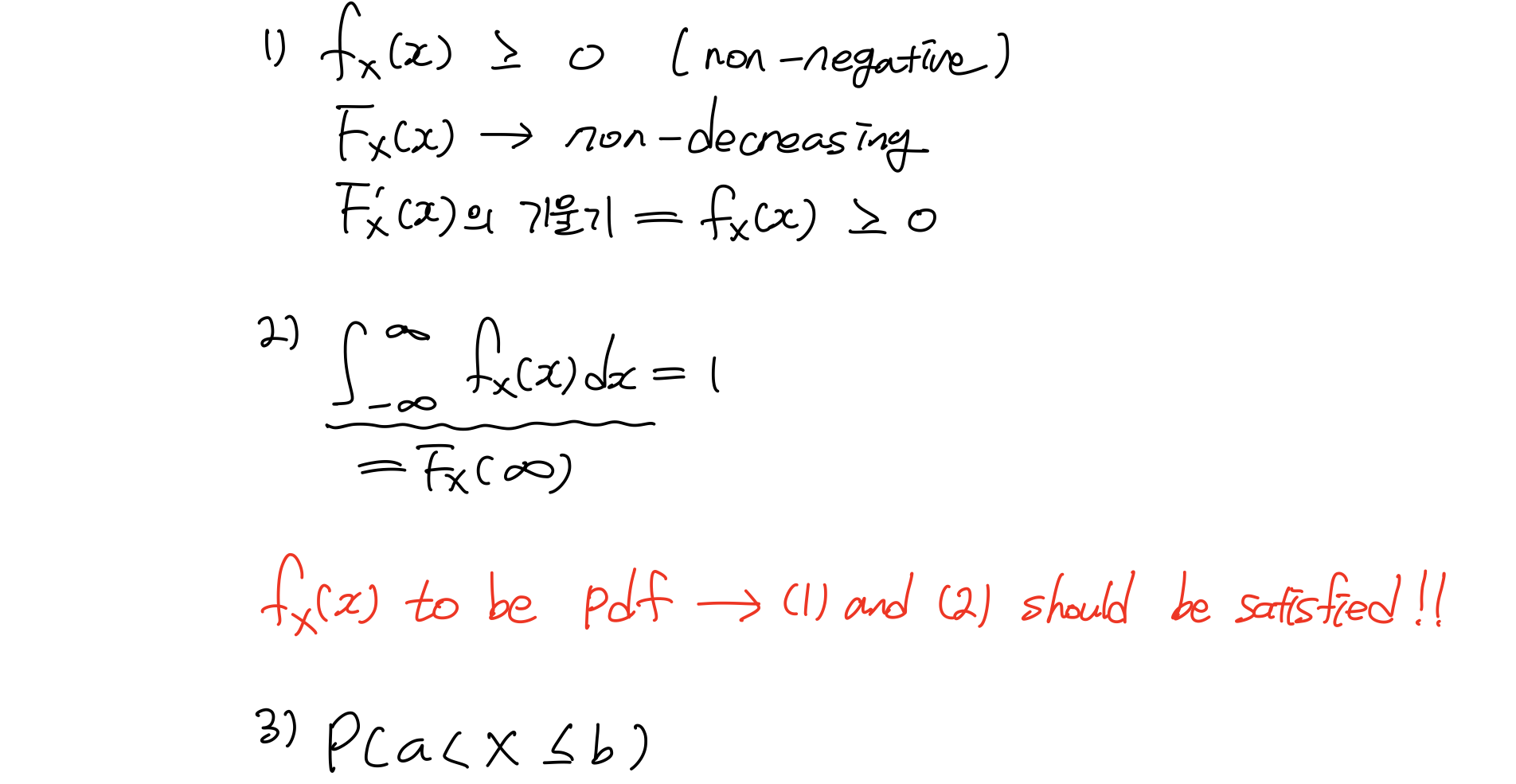
Uniform distribution

우리가 말하는 음성, 오디오 시그널은 시간 축에 대한 전기적인 파형(wave form)으로 표현이 된다. 처음의 파형을 continuous 혹은 analog라고 한다.

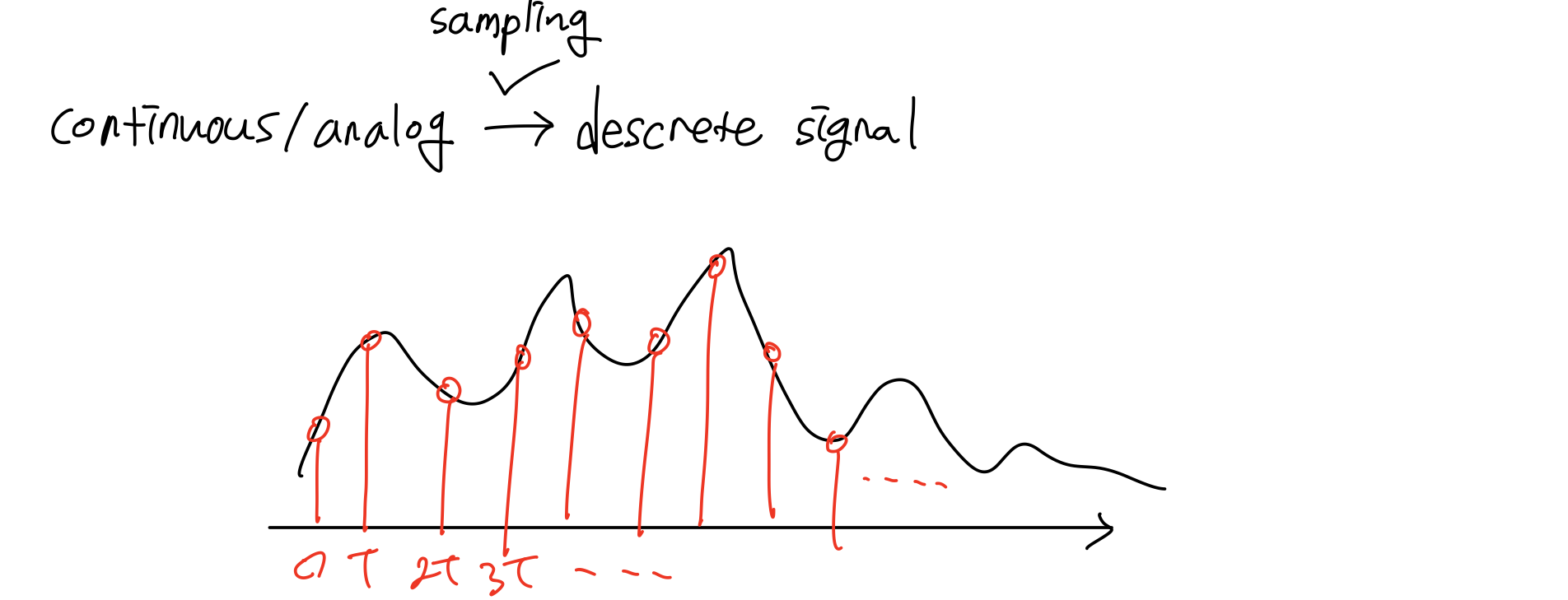
이것을 일정한 시간 간격으로 파형의 높이 값을 뽑아내는 것을 discrete signal이라 한다. 이때 이 과정을 표본화 혹은 Sampling 이라 한다. 그렇기 때문에 파형을 복원할 때는 원래의 파형과 다른 형태의 파형이 나오게 된다.

유선통화 경우는 8kHz, 오디오 시그널은 44.1kHz 주파수로 sampling한다. 사람이 들을 수 있는 가청 주파수는 20kHz 정도 된다. frequency 최대값의 두배 이상으로 하면 오리지널 시그널을 완벽하게 복원할 수 있다고 수학적으로 증명이 되어있다고 한다.

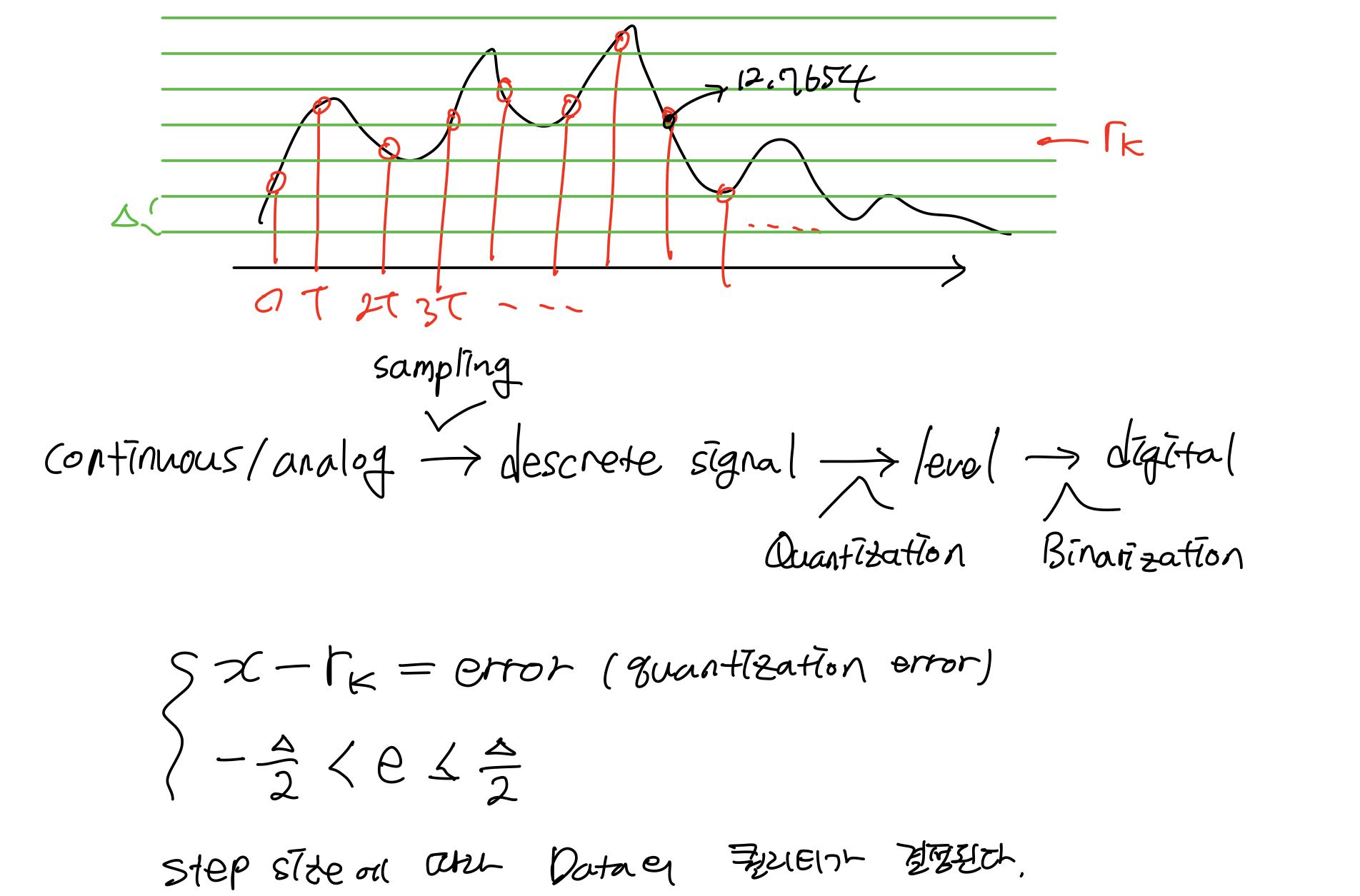
문제는 coninuous 시그널이기 때문에 descrete 데이터가 너무 방대하다. 따라서 일정한 구간으로 나누어, 그 구간안에 값이 들어오면 대표값으로 값을 바꾸어준다. 이 과정을 Quantization 양자화 라고 한다. 이렇게 나온 level 값을 binarization 이진수화 하면 digital 이다.