"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 확률과통계 수업을 정리한 내용입니다.

Review

Continuous RV는 특정 x에 대한 확률 자체를 정의하기가 어려우니, CDF를 미분해 얻어지는 density를 정의해 확률 대신 사용하는 개념인 PDF.

1. Moment of RVs

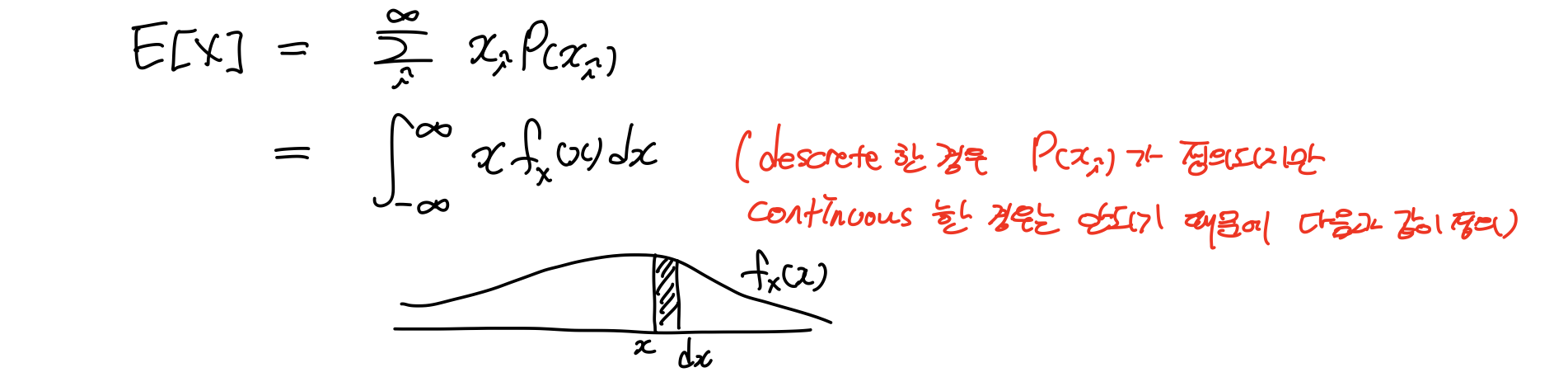
1.1 Expectation(mean)

descrete하면 확률 P(x)에 대해 정의할 수 있지만, continuous RV는 정의할 수 없기 때문에 PDF를 이용해 정의한다.

1.1.1 Possion distribution

발생한 사건 수에 대한 확률을 다루는 문제는 Possion distribution이다. 이때 확률분포는 descrete RVs을 띄고있다.

1.1.2 Exponential distribution

확률분포가 Exponential 함수의 형태를 띄고 있는 경우이다. 그리고 Continuous RVs 경우이다.

위의 두 예제를 통해 Parameter(ramda)만 알면 수학적으로 모델링이 가능하다. 따라서 parameter를 구하는 것을 Parametric probability density estimation이라 부른다. 구하고자 하는 랜덤한 현상들이 어떤 형태의 확률분포를 갖는지 구하고자 할때, parameter를 구할 필요가 있을 때는 확률분포가 정해지는 것이고 parameter가 정해지지 않을 때는 특정한 확률분포를 정하기 어려울 때이다.

1.2 Moment of RV

1.2.1 n^th order moment

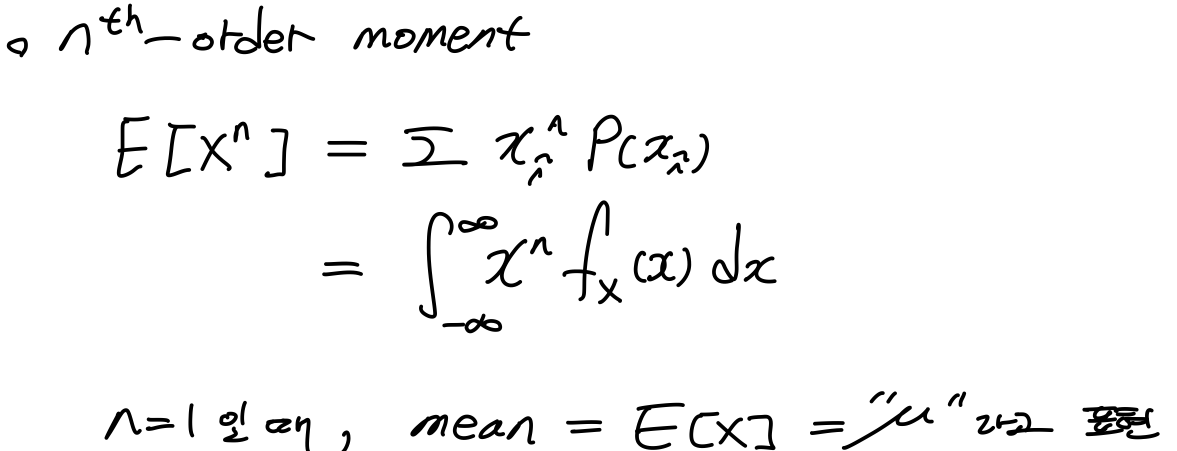
X라는 RV는 어떤 랜덤한 experiment에 outcome에 대응하는 하나하나의 확률 값을 갖는다. 그럼 X^n은 어떻게 되느냐? X와 같다. 주사위를 예를 들면, 주사위를 던져 어떤 숫자가 나와도 확률은 1/6이다. 주사위 숫자(1,2,3,4,5,6)을 제곱승해도 그 확률은 같다. 따라서 Descrete RV의 경우, 그 확률값은 여전히 X와 같다.

1.2.2 Central momnet

Moment는 물리학에서 무게중심이라 할 수 있는데, 확률에서는 결국 평균을 이야기 한다. 결국 어떤 데이터에서 평균을 구하느냐 문제.

예제

이항정리에서 수열의 합을 미분해서 계수의 합을 구하는 것에 대해,