"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.

Null Space

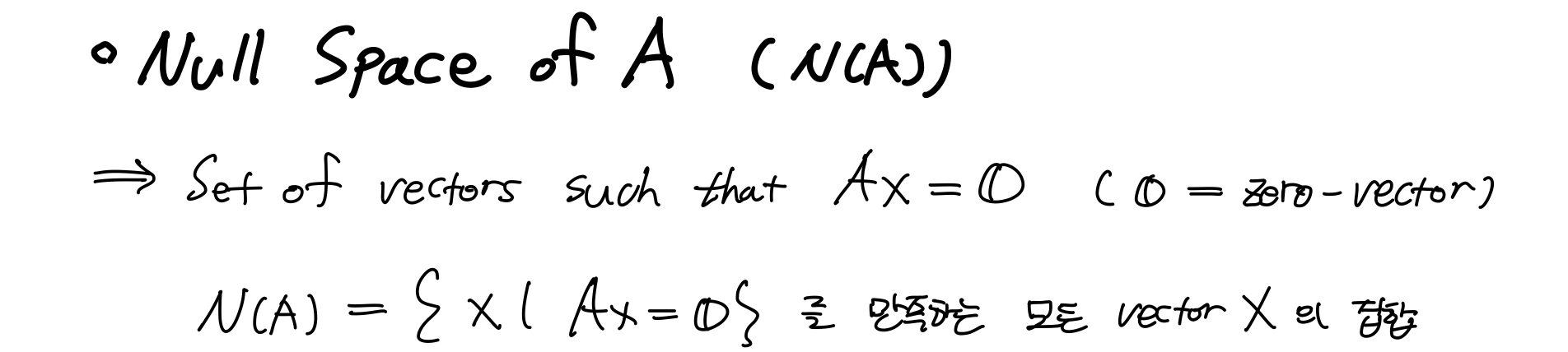
집합이지만 다음의 조건을 만족해야 Space라고 할 수 있다.

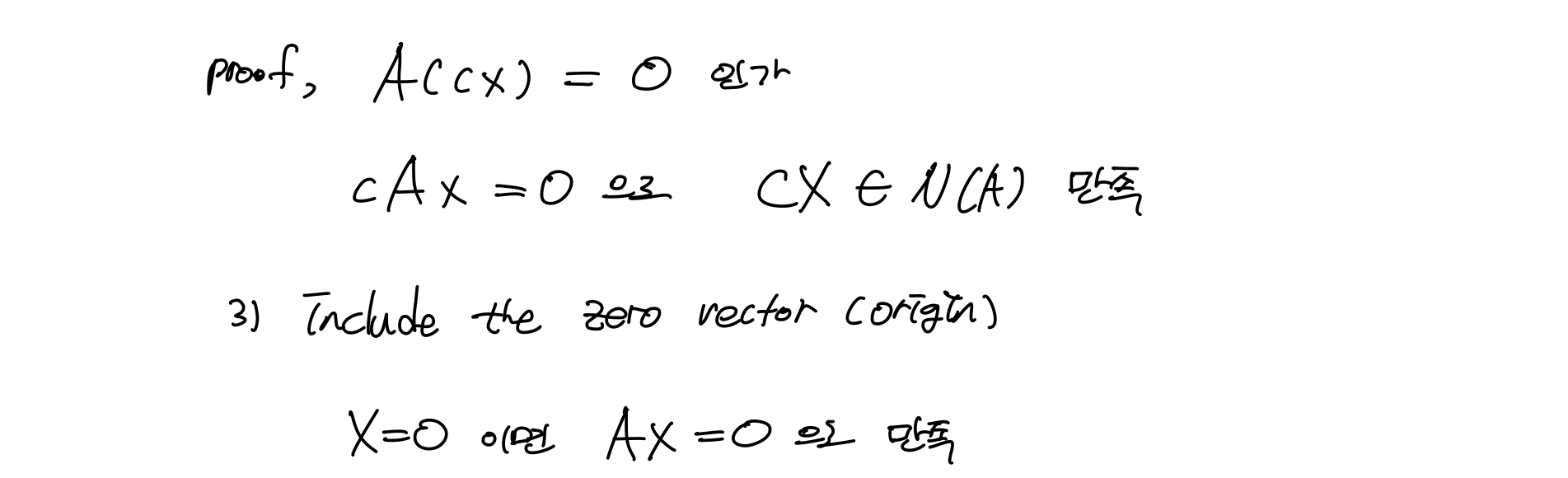
Null Space가 무엇인지 다음의 예를 통해 알아보자.

Solving Ax=0 & Ax=b

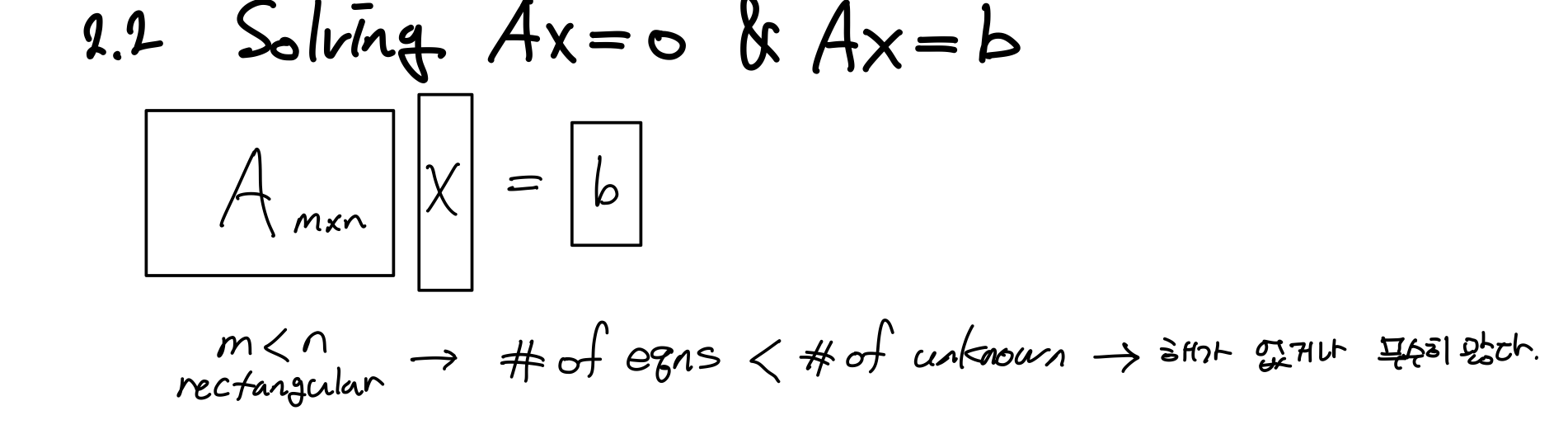
Echelon form U

해를 구하는 방법으로 가우스소거법을 통해 A와 b에 해당하는 행렬만 변화시켜주면 된다. 다만, b 행렬은 0벡터이므로 굳이 X행렬=Null Space를 구할 때는 A행렬만 가지고 계산하면 된다.

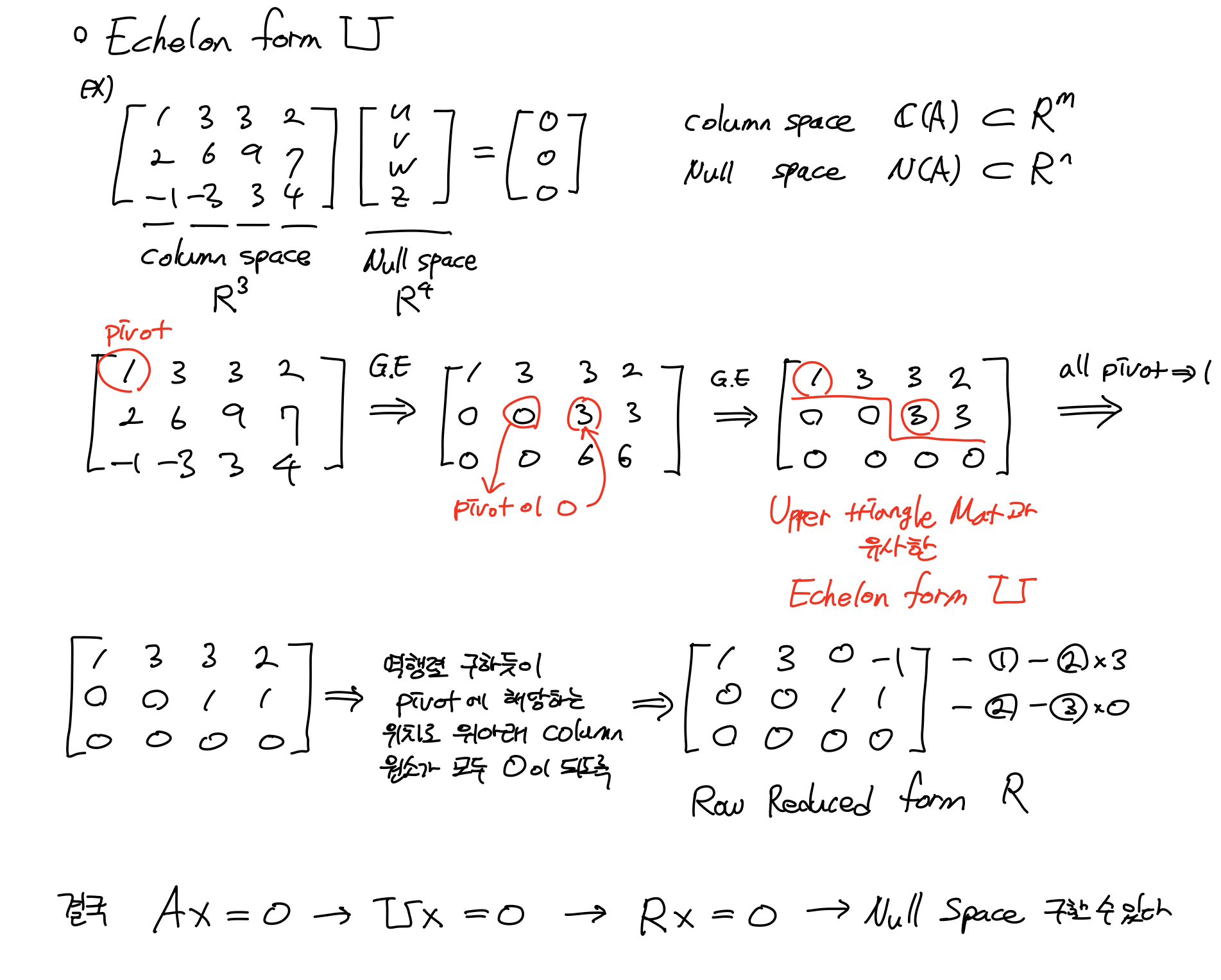
결국 Rectangular한 system(미지수의 수가 더 많은 system)에서도 Gauss Elimination 형태로 해를 구할 수 있다.

1장에선 Squre Matrix를 Gauss Elimination으로 풀면 해가 있거나(Inverse Matrix가 존재) 해가 없거나 했다. 2장에서 Rectangular Matrix도 해가 무수히 많거나 해가 없다. 하지만 무수히 많은 해 집합은 자체적으로 Vector Space를 구성한다.

이제 위에서 구한 Raw Reduced form R을 보면 아래의 형태가 된다. 이때 pivot이 존재하는 column의 변수(u w)를 pivot variable이라고 한다. 그리고 나머지 변수는 free variable이라 한다.

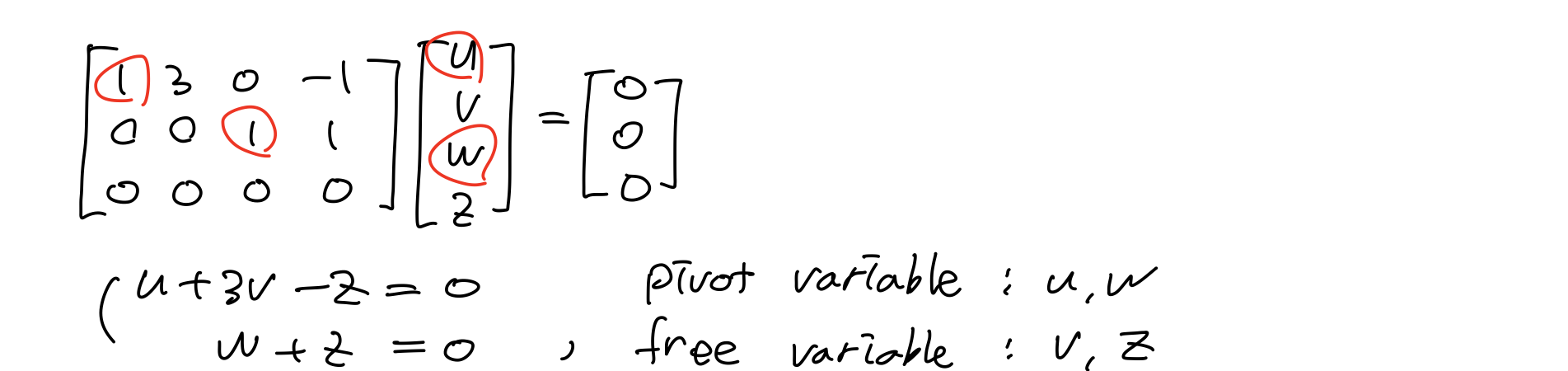
그리고 pivot variable을 free variable로 표현하여 정리하면 다음과 같은 linear combination 형태로 정리할 수 있다.

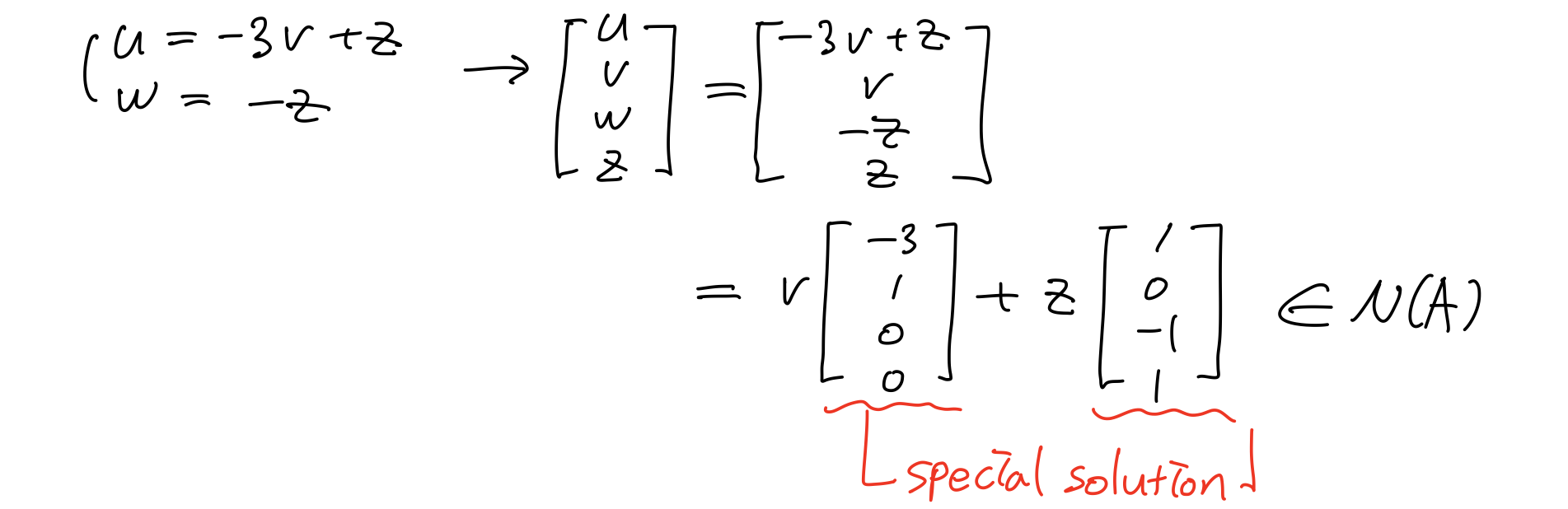
이는 u,v,w,z의 4차원에 Null Space를 구성하는 X vector 구하는데, 그 결과가 위의 임의의 linear combination이다. 그리고 linear combination은 free variable로 구성된다. 이를 통해 정형화된 solution을 구할 수 있다.

그리고 special solution은 다음의 특징을 갖는다.

그러나 미지수 수와 그것을 표현할 수 있는 special solution vector의 차원이 맞지 않는다. 그래서 vector space에 대해 Dimension을 정의해야 한다.