"모두를 위한 열린 강좌 KOCW"에서 제공하는 한양대학교 이상화 교수님의 선형대수 수업을 정리한 내용입니다.

1. Review

1.1 Ax=0

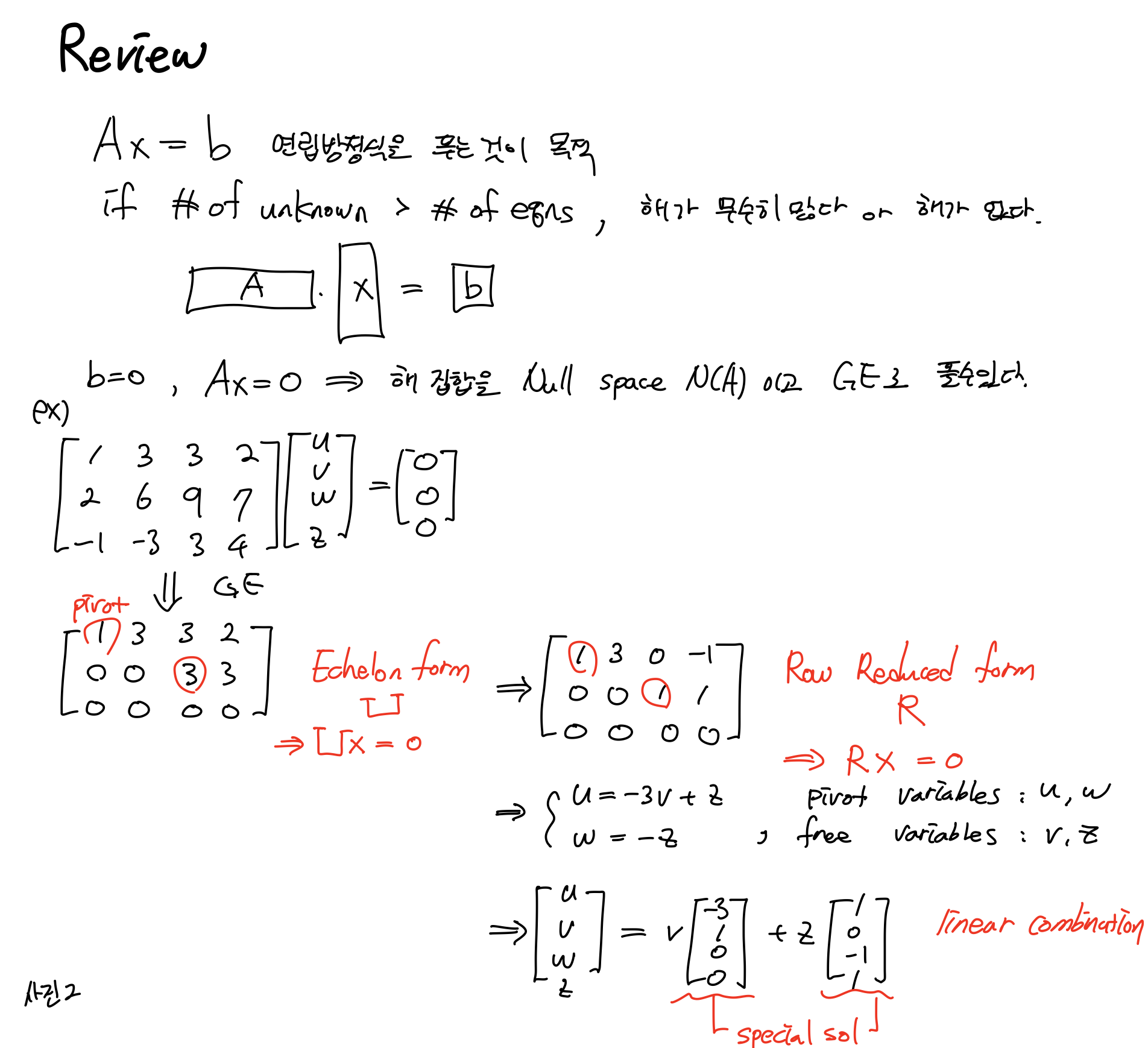
1.2 Ax=b

이번에는 Ax=b (b!=0) 연립방정식에 대해 알아보자.

이때 Ax=b에서 b는 A의 column vector의 linear combination이다. 즉 b가 column vector space A에 속해야 sol이 존재한다. 그런데 b는 example에서 b3-2b2+5b1=0 조건을 갖는다. 이 말은 b1,b2,b3를 x,y,z 처럼 공간좌표라고 생각하면 조건은 원점을 지나는 평면의 방정식이 되고, 따라서 column vector의 조합이 평면 위 점이 되어야 한다.

조건을 만족하는 임의의 b vector를 정해 설정한다.

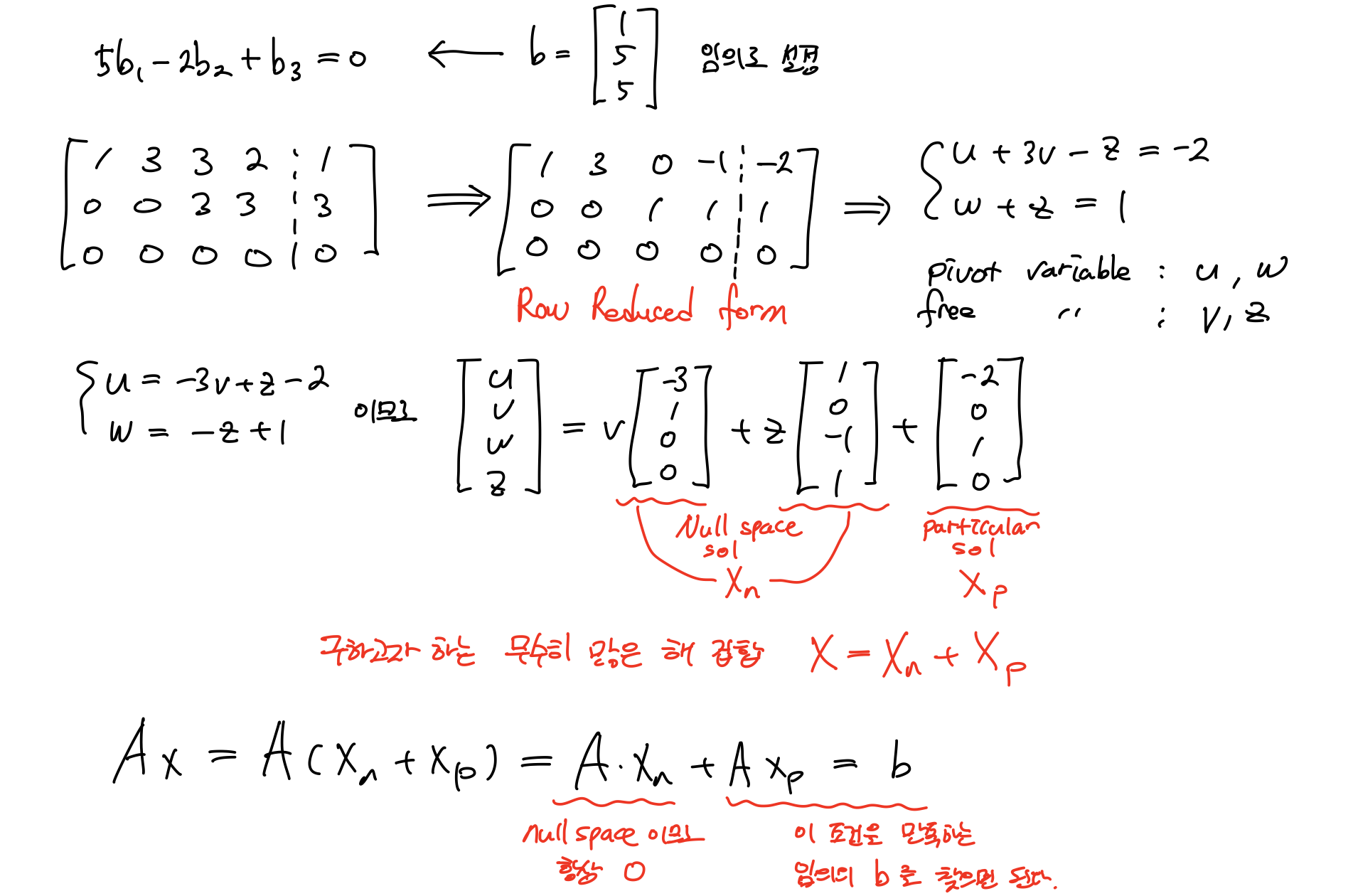
Null space sol Xn 조합에 particular sol Xp를 더한 것이 우리가 구하고자 하는 무수히 많은 해 집합 X이다.

free variable로 구성된 linear combination은 4차원 공간안에 평면을 나타낸다. 그 값에 particular sol을 더한 것. 따라서 원래는 원점을 지나는 평면이지만 Xp만큼 평행이동한 평면이 된다.

1.3 정리

2. Linear Independence Basis(vectors), Dimension

2.1 linear independent

2.2 Rank of A

아래의 숫자를 뜻하는 Rank.

2.3 Spanning

Span은 어떤 벡터를 가지고 온갖 종류의 linear combination을 해서 vector space을 만들어 내는 것을 말한다. 그때 vector는 vector space를 span한다. 그런 의미를 가지고 있다.

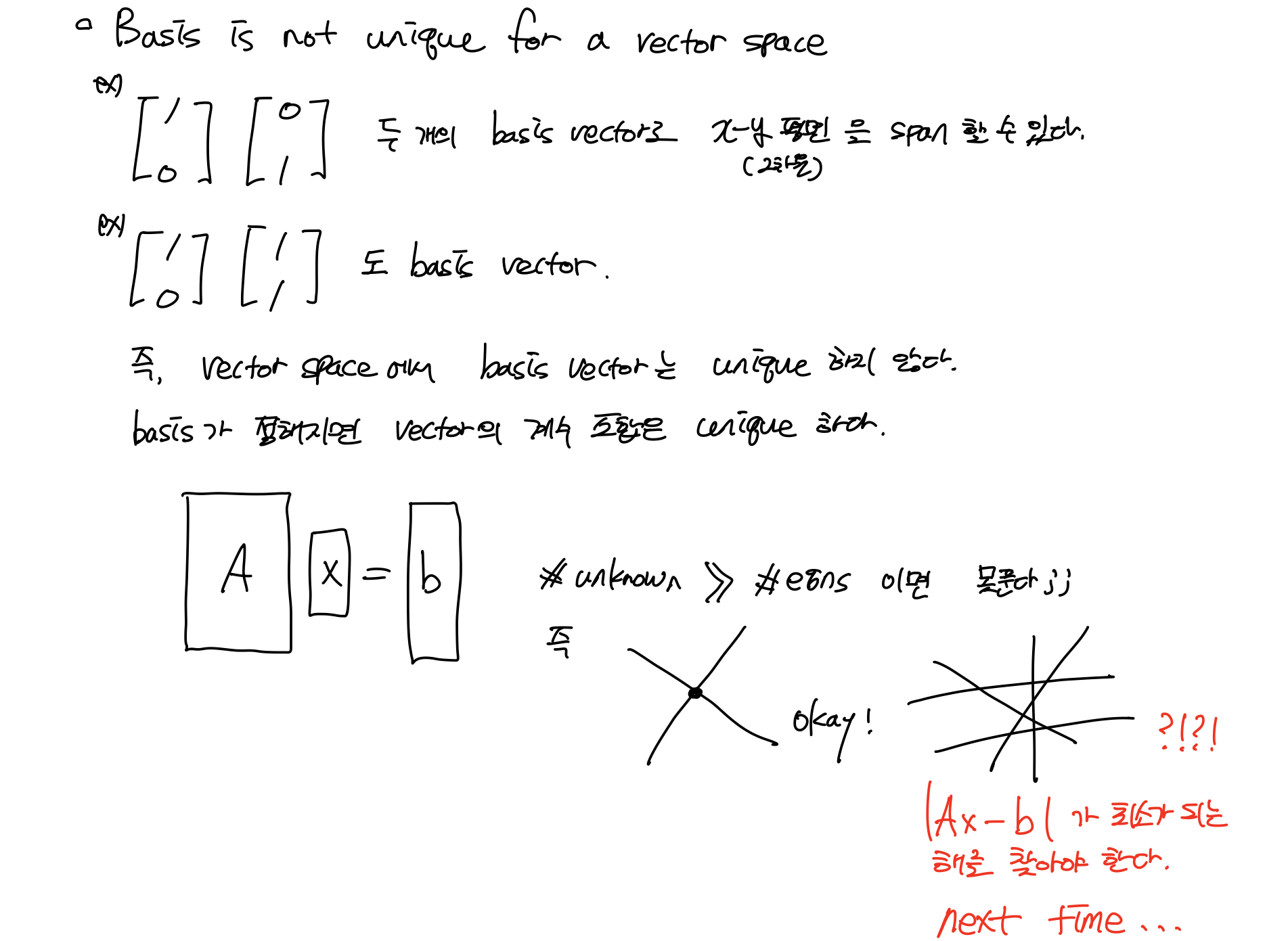
단, 위의 ex) 와 같이 같은 vector space를 span 하더라도 vector 조합은 unique 하지 않다. 그럼 언제 linear combination이 unique하냐 혹은 unique 하지 않나 확인할 수 있을까?

2.4 Basis (vectors)

linearly independent vector의 최소한의 수. 어떤 vector space를 span하는 basis를 구해야 한다면, linearly indepdent한 vector로만 구성하면 된다. 이때 그 숫자가 minimum 되어야 한다. 이것을 basis라고 한다.

이전에 예로 들었던 같은 vector space(x-y평면)을 나타내는 vector를 보면, 첫번째와 두번째 예는 unique 지만 세번째는 조합이 unique하지 않다.

지금까지 Ax=b 선형연립방정식에서 무수히 많은 해를 vector space라고 하는 Null space를 활용해 solution을 구했는데, 그 외 다른 vector space는 가급적이면 linearly independent한 vector가 최소가 되는 것이 몇 개인지 알면 해 집합의 차원을 알 수 있다.

2.4.1 Basis is not unique for a vector space