이번 강의는 "Recurrent Neural Networks"에 대한 강의이다. 이름에서 알 수 있듯이 recurrent 무언가 반복되는 network라는 것을 알 수 있다.

Recurrent Neural Network

첫 번째로 던지는 화두는 "만약 입력 데이터의 크기가 다양하다면?"이다. 지금까지는 모든 입력 데이터의 크기가 같은 Dimension을 가지고 있었다. 예를 들어, 입력 데이터가 이미지라면 255*255 사이즈의 입력데이터였다. 하지만 문장, 소리, 비디오 이미지와 같이 각 데이터의 크기가 다른 경우를 생각해보자.

가장 단순한 아이디어로는 zero-pad를 이용해서 모든 데이터의 사이즈를 맞추는 것이다. 이때 시퀀스가 가장 긴 데이터를 기준으로 해서 맞춘다. 가장 단순하고 동작이 가능하지만 문제가 있다.

Problem: 매우 긴 시퀀스의 경우에는 성능이 좋지 않다.

이유 역시 쉽게 알 수 있다. 많은 zero-pad에 의해 불필요한 정보가 많아지기 때문에 모델의 성능에 악영향을 미친다.

Idea: 각 레이어에 하나의 입력이 주어지면 어떨까?

다양한 사이즈의 입력 데이터를 다루기 위해 각 레이어에 각 입력 데이터를 주어지면 어떨까 하는 아이디어이다. 시퀀스 데이터의 특성 상 이전 데이터의 정보가 다음 데이터에 영향을 미치기 때문에 입력 데이터는 (이전 레이어의 출력, 현재 레이어의 입력)이 된다.

각 레이어에 입력 데이터를 주어주는 것은 시퀀스의 길이에 따라 가중치 총 수가 증가한다. 이 말은 시퀀스의 길이가 짧으면 평가해야 하는 레이어의 수가 줄어든다고 볼 수 있다.

Problem: 따라서 문제는 시퀀스의 길이에 따라 학습해야 하는 가중치 행렬의 수가 증간하다는 것이다.

가중치 행렬의 수가 시퀀스의 길이에 따라 증가한다는 문제를 해결하기 위한 아이디어가 있다.

Solution: 각 레이어의 가중치 행렬을 공유하는 것.

모든 레이어의 가중치 행렬을 공유하면, 주어진 데이터에 Overfitting(오버피팅)이 될 수 있는거 아닐까 하는 걱정이 든다. 하지만 가중치 행렬을 공유한다는 것은 결국 Parameter의 수를 줄이는 것이고, 따라서 모델이 더 단순해지고 Overfitting을 방지한다고 볼 수 있다.

이로 인해서 레이어를 더 깊게 쌓을 수 있다.

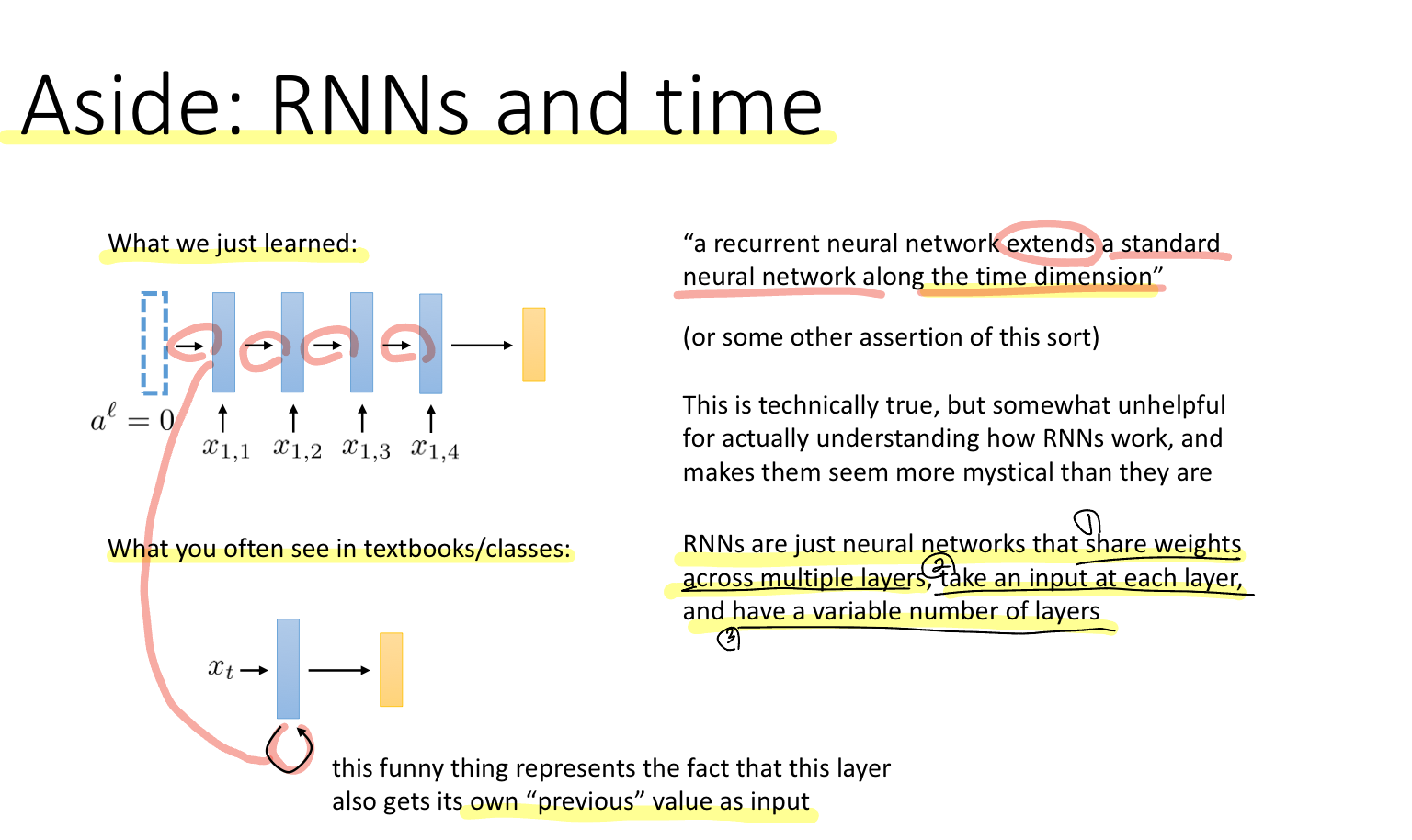
한편, RNN(Recurrent Neural Network)은 단순 RNN을 시간에 대해 확장하는 network라고 볼 수 있다.

결국 RNN은
1) Share weights across multiple layers. 여러 계층에 대해 가중치를 공유
2) Take an input at each layer. 각 계층(레이어)에 따라 각 입력 데이터가 존재
3) 가변적인 계층(레이어)를 갖는 신경망.

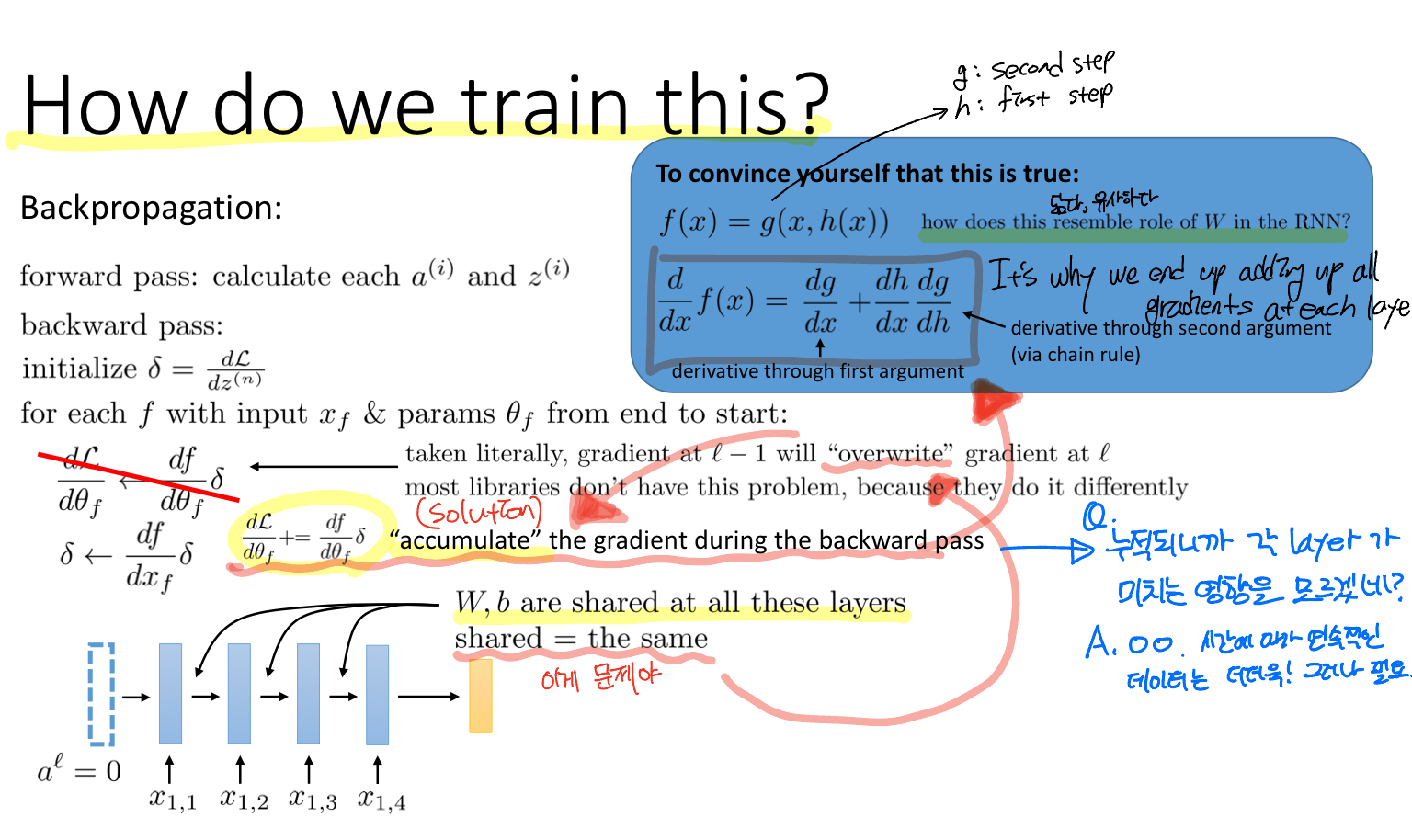
Q. How do we train this? 어떻게 학습하는가?

기존의 역전파 학습은 Upstream derivative(상위 레이어의 미분, 즉 gradient)을 반복적으로 업데이트하는 방식인데, RNN 구조는 각 레이어에 하나의 입력 데이터가 주어지며 모든 레이어는 가중치 행렬과 bias를 공유한다. 따라서 이전 레이어의 gradient가 다음 레이어를 "overwrite"하게 된다.

Problem: Overwrite gradient

이 문제를 해결하려면 기존 방식과 다르게 gradient를 누적하는 방식을 제안한다.

Solution: Accumulate the gradient during the backward pass

근데 이 해결방식이 새로운 아이디어가 아니라 당연하다고 한다. 근데 레이어에 두 개의 입력 데이터 (이전 레이어의 출력 hidden_state, 현재 레이어의 입력 input)가 주어지면, 그에 대한 derivative를 구하면 이전 레이어의 gradient가 누적되는 형태가 되는 것을 우측 상단의 파란색 박스를 보면 알 수 있다.

만약 출력 역시 다양한 크기라면?

두 번째 화두는 입력에 이어서 출력 역시 크기가 다양한 경우에 대해서 생각해보자.

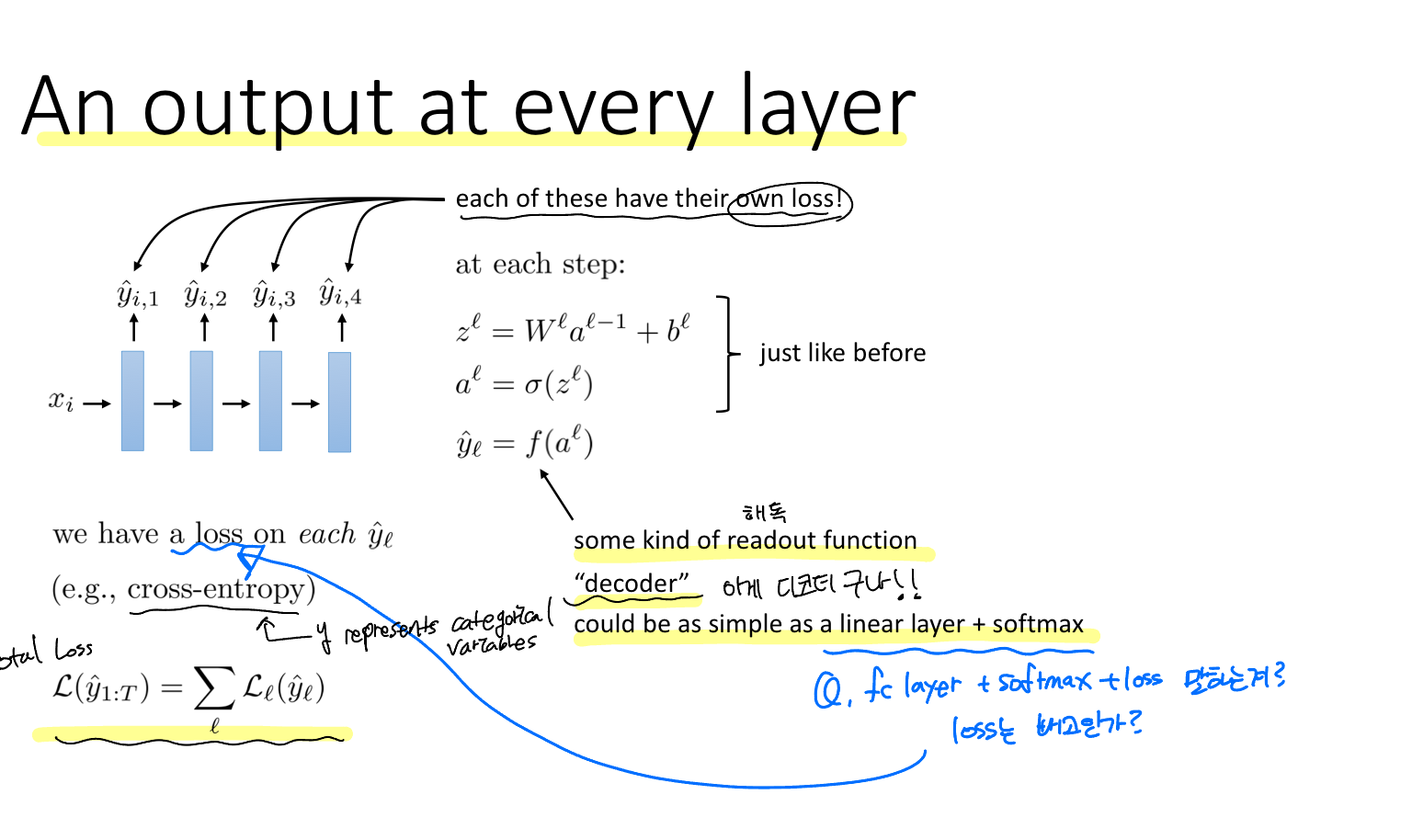
그렇게 되면 각 레이어는 하나의 입력(이전 레이어의 출력)과 두개의 출력(손실함수와 다음 레이어로의 출력)을 갖는다. 이때 각 출력은 각각의 Loss (손실함수)를 갖는다. 또한 이때 출력함수를 decoder라고 한다. 이전에 보았던 Fully connected layer + softmax를 말한다.

또한, 이 모델의 total loss는 각 레이어의 loss의 총합이다.

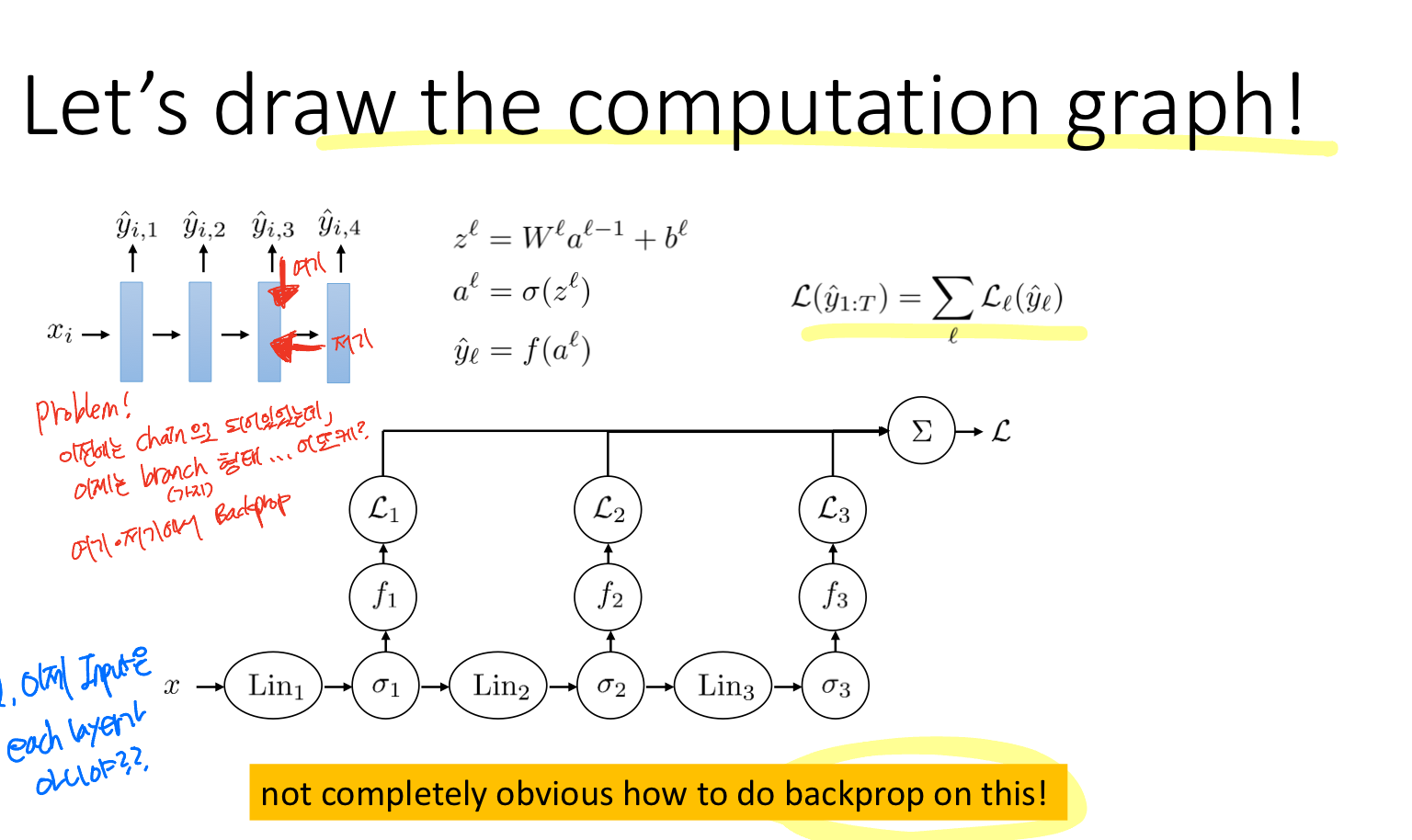
이 구조를 computation graph로 나타내면 위와 같다. 보면 알 수 있듯이 이전과 달리 backprop를 수행하는 게 쉽지 않아 보인다.

Problem: chain 구조가 아닌 branch 구조의 Backpropagation은 어떻게?

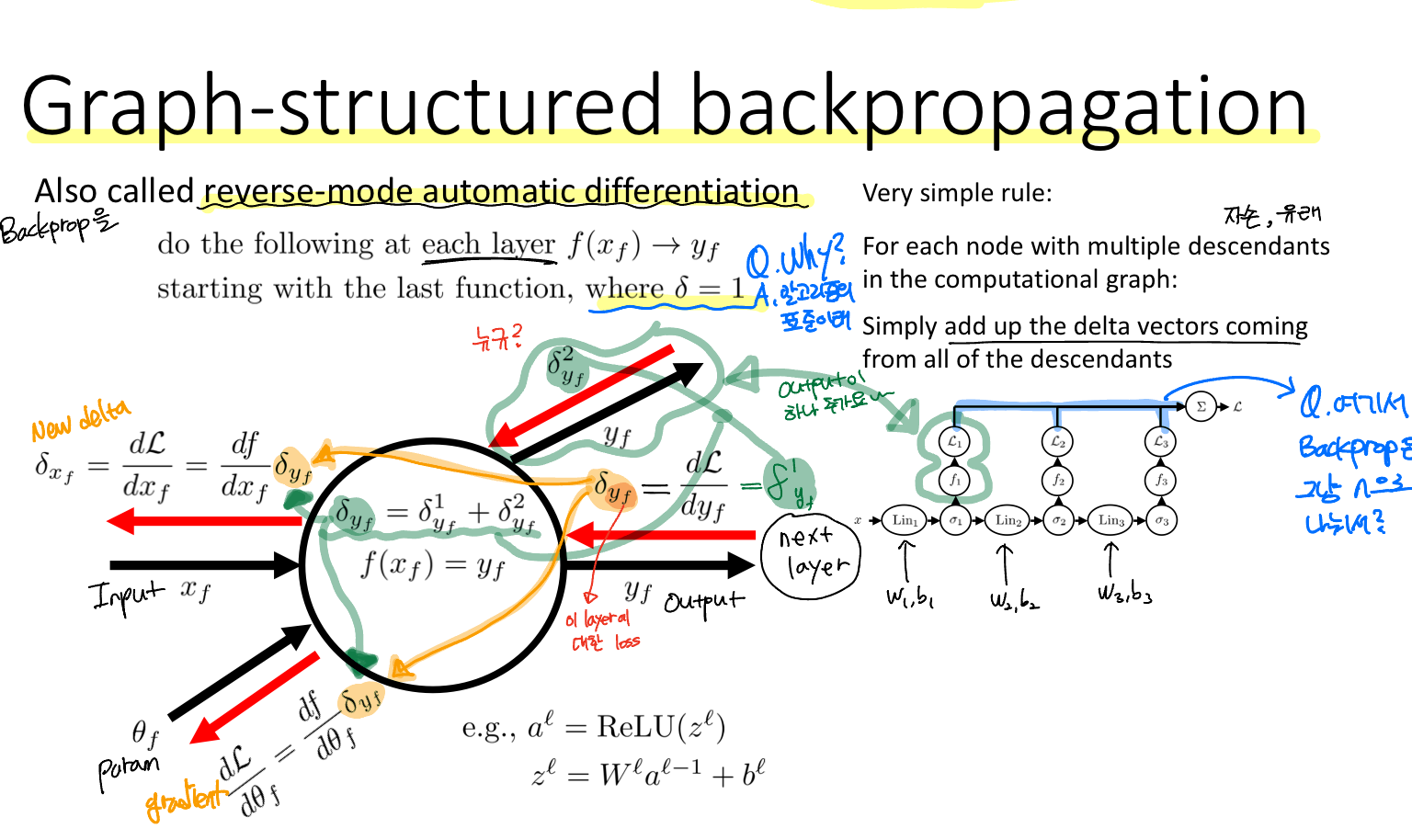
Backpropagation을 reverse-mode automatic differentiation이라고 부르기도 한다.

위의 노드는 임의의 레이어의 구조를 나타내고 있는데, 하나의 입력과 파라미터가 들어오고 두 개의 출력이 있다. Backprop pass 역시 "derivative of Loss with respect to each loss"와 "derivative of Loss with respect to next layer"로 구성되어 있다.

그리고 multiple descendants로부터 받은 gradient의 합산이 다음 레이어의 Upsteam derivative가 된다. 이로부터 입력과 파라미터에 대한 gradient를 구할 수 있다.

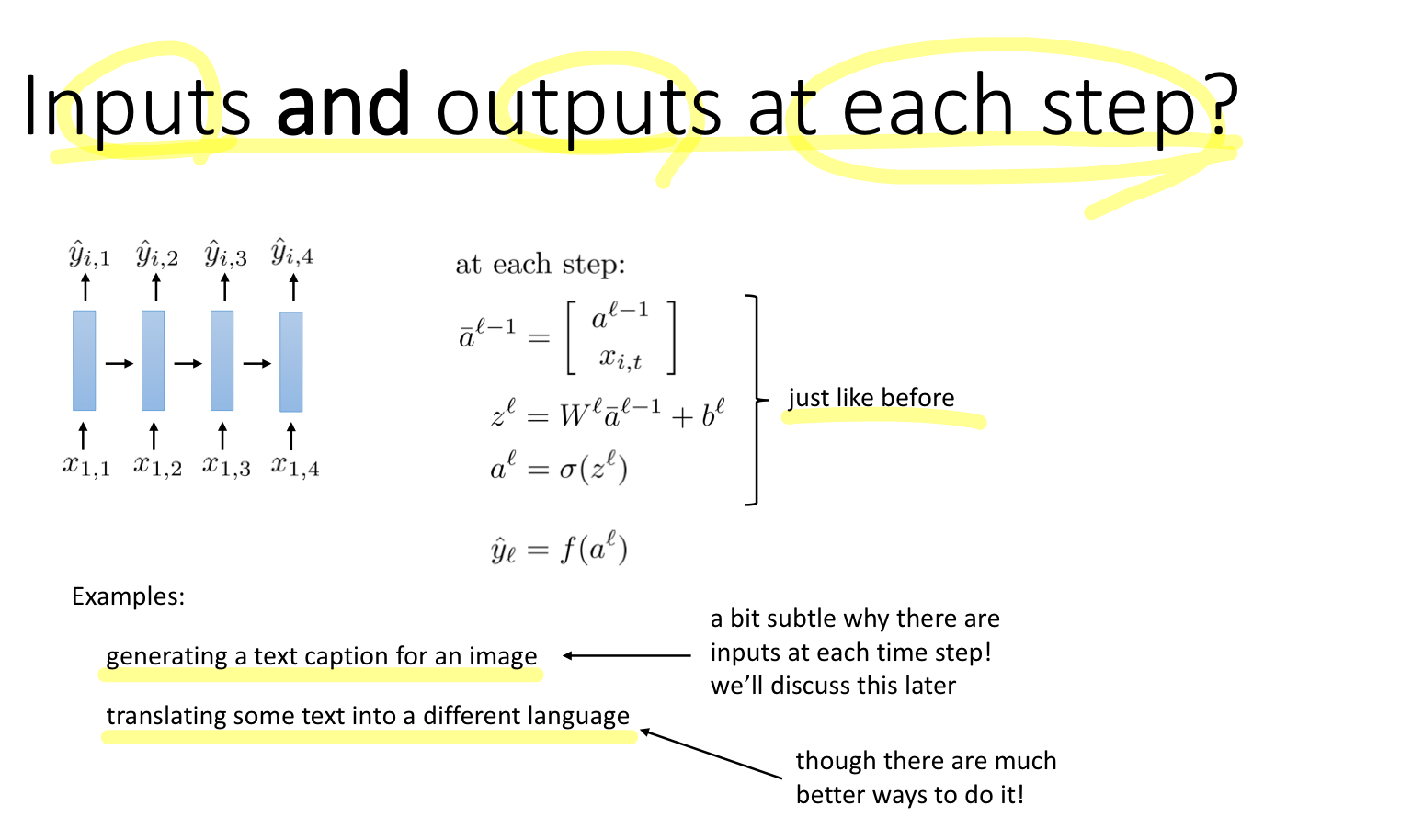
처음에는 입력 데이터의 사이즈가 다양한 경우, 그리고 출력 사이즈가 다양한 경우에 대해서 알아보았다. 매 스텝마다, 즉 각 레이어마다 입력과 출력이 있는 경우를 다뤄보면 위와 같다. 이때 입력 데이터는 이전 레이어의 출력과 현재 레이어의 입력으로 구성되어 있고, 출력은 각 레이어마다 하나의 출력이 존재하며 각각의 Loss가 존재한다.

이러한 구조의 모델은 이미지를 입력으로 넣으면 텍스트가 생성되는 task, 혹은 번역 업무가 있다.

What makes RNNs difficult to train?

이번에 다룰 내용은 RNN 구조의 학습을 어렵게 만드는 것이 무엇인가?에 대한 내용이다.

일반 딥러닝 모델과 같이 RNN 모델 역시 학습 층이 깊어질 때 발생하는 문제가 존재한다.

Problem: gradient vanishing으로 인해 초반부분의 정보를 잊어버리게 된다

교수님은 vanishing gradient의 경우는 큰 문제를 야기하지만, exploding gradient는 gradient clipping으로 어느정도 해결이 된다고 한다.

여기서 gradient clipping은 gradient가 threshhold 이상이 되면 학습은 중단하는 스킬을 말한다.

기본적인 아이디어는 이전과 유사하게 자코비안, 즉 gradient가 1에 가깝게 만드는 것이 있을 것입니다.

이를 위해 각 레이어의 (입력 - linear layer - activation)을 하나로 묶어 "RNN dynamics"로 둔다. 따라서 이것에 대한 자코비안 행렬이 identity matrix가 되면 gradient vanshing 문제를 해결할 수 있을 것이다.

하지만 이는 매번 좋은 것만은 아니라고 합니다. 왜냐하면 기억하고 싶은 것과 잊고 싶은 것을 구분해야 하기 때문입니다. 이는 문장의 모든 걸 기억할 필요없이 핵심 키워드를 기억하는 것이라고 볼 수 있다고 생각한다.

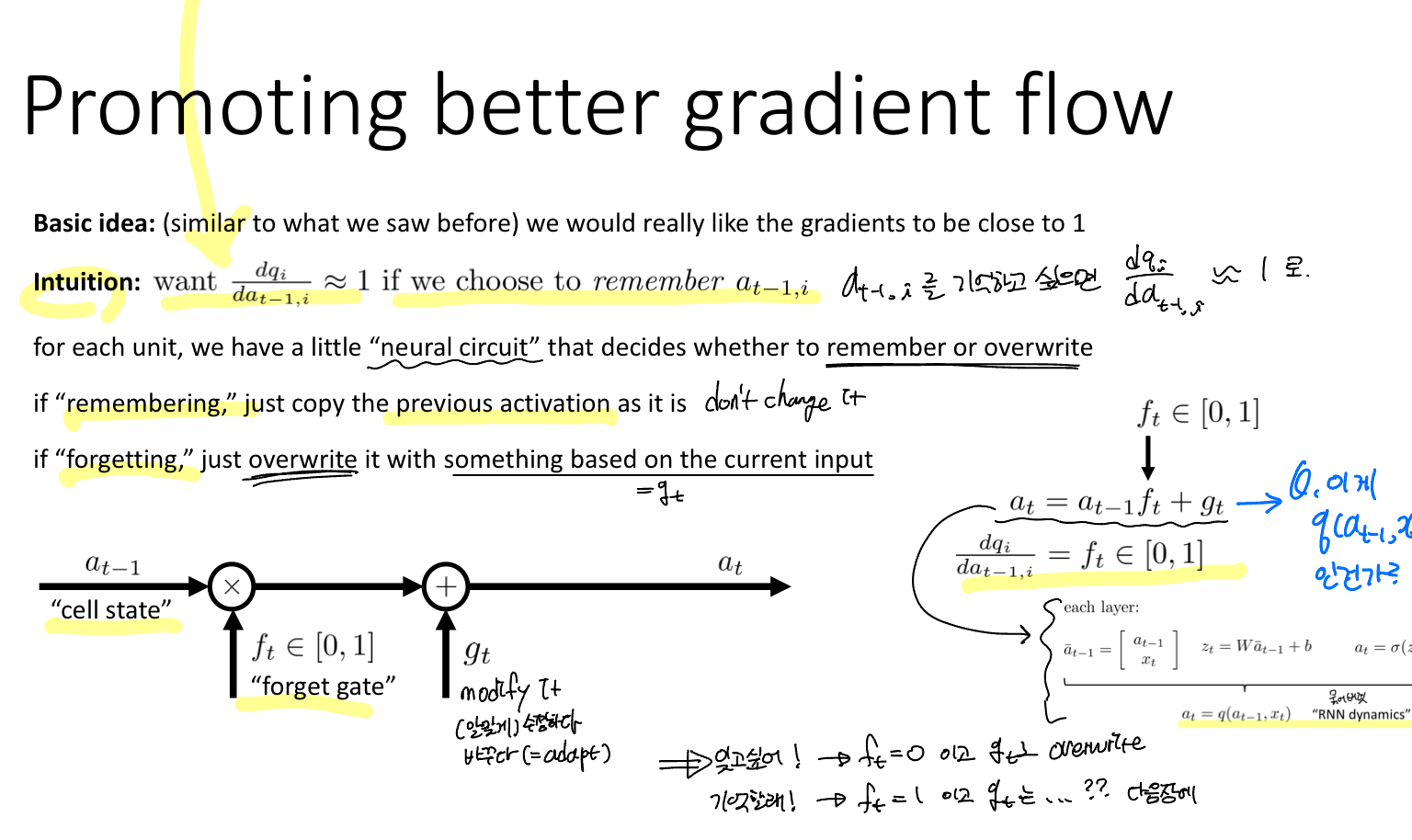
i번째 데이터를 기억하고 싶다면, "neural circuit"이라고 부르는 i번째 자코비안 행렬을 이용한다. 만약 기억하고 싶다면 이전 레이어의 활성화 값을 그대로 사용하고, 잊고 싶다면 현재 입력에 의한 값으로 덮어쓴다.

Idea: 이전 레이어의 정보(활성화 값)을 얼마나 기억할 것인가를 결정하는 "forget gate". 그리고 얼마나 잊어버릴 것인지 = 얼마나 덮어쓸 것인지를 결정하는 "overwrite gate"

이 두 게이트를 통과한 결과가 다음 레이어의 입력으로 들어가는 것이다.

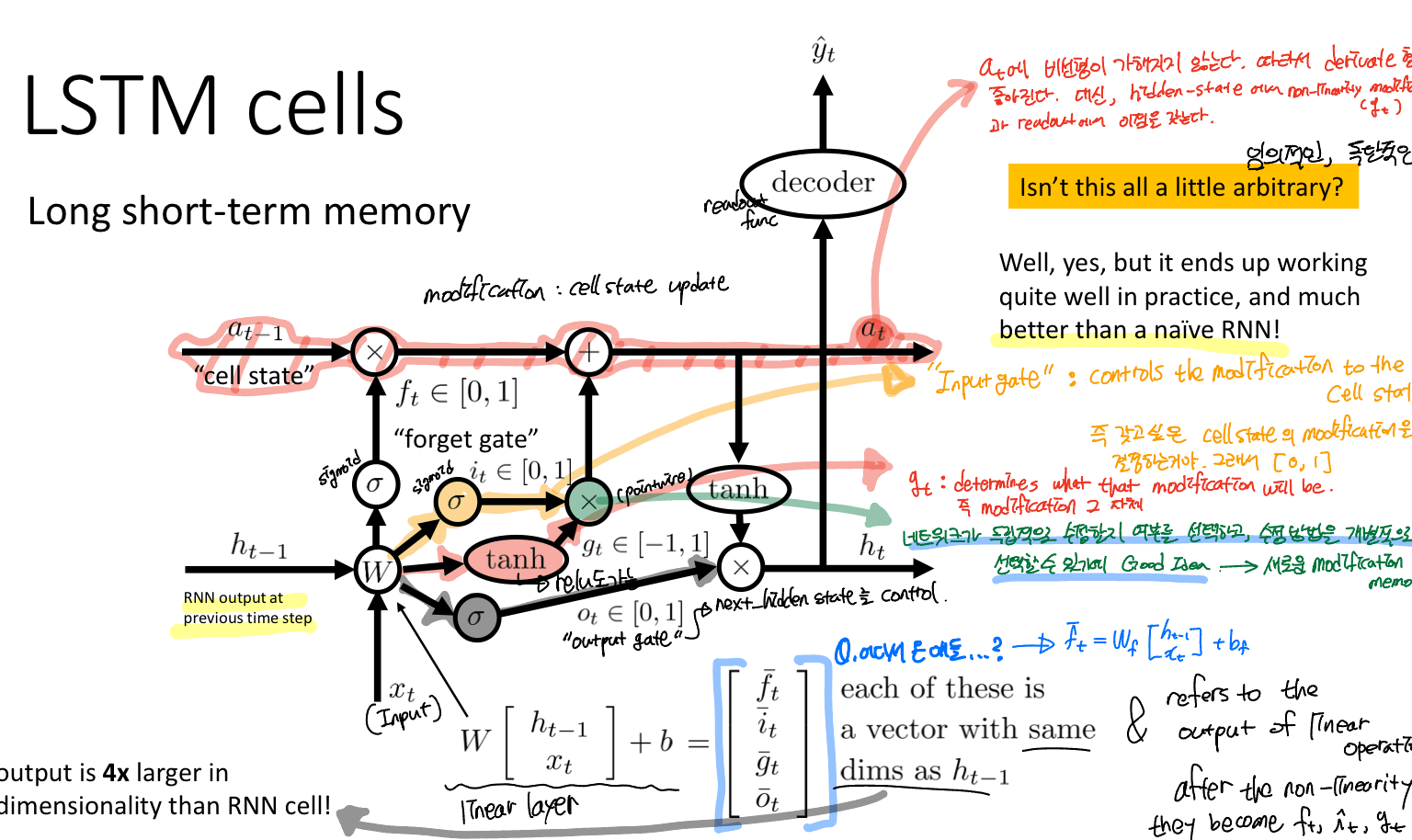
이것이 바로! LSTM (Long Short-Term Memory). 이름 그대로 장단기 메모리, 기억할 것과 잊어버릴 것을 선택해서 잘 기억하겠다!!

Forget gate (f): 셀 상태에서 어떤 정보를 버릴지 결정
Input gate (i): 셀 상태에 어떤 새로운 정보를 저장할지 결정
Output gate (o): 셀 상태에 따라 출력할 내용을 결정
Cell gate (g): modification, Cell_state에 추가할 수 있는 새로운 후보 값의 벡터를 생성

이때 next Cell_state를 보면 비선형이 가해지지 않는 것을 알 수 있다. 이는 backward pass 과정에서 derivative를 구하는 것이 편해진다고 볼 수 있다. 즉, 이전 레이어의 활성화 값이 그대로 사용한다고 볼 수 있다.

앞에서 말했듯이 Cell_state를 구하는 과정에서 비선형이 가해지지 않는 선형적이기 때문에 장기 의존성을 갖는다. 따라서 우리는 Cell state를 "long term" memory. 그리고 Hidden sate를 "short term" memory라고 부른다.

Using RNNs

여러 개의 출력이 필요한 대부분의 문제(예를 들어 텍스트 생성)은 출력 간에 강한 종속성 갖는다. 이를 Structured prediction 구조화된 예측이라고 한다.

Problem: 때때로 확률이 정확하더라도 말도 안되는 결과가 나옵니다.

이는 단어 간의 covariance가 정확한 단어를 예측하는 것만큼 중요하기 때문입니다. 즉, 단어 간의 관계를 고려해야 한다는 뜻입니다.

Solution: 이전 레이어의 출력이 이후 출력에 대해 영향을 끼쳐야 한다

즉, 이전 레이어의 출력을 다음 레이어의 입력을 주어주는 것입니다. 이는 단어 간의 covariance를 구하는 것은 아니지만, 시퀀스 데이터에서 연속적인 요소들 사이의 의존성(dependencies)를 모델링하는 매커니즘이라고 볼 수 있습니다.

그런 관점에서 보니 헤드라인이 왜 Autoregressive models and structured prediction인지 알겠다. 단어 간의 시퀀스적 관계를 학습, 즉 연속적인 데이터 포인트 사이의 조건부 확률이다.

Problem: How do we train it?

그럼 어떻게 학습해야할까? 각 레이어의 입출력이 각각 존재하기 때문에 결국 입력 데이터는 그대로 시퀀스를 사용하고, 답지(ground truth) 역시 그대로 시퀀스를 사용하되 하나씩 shift한다.

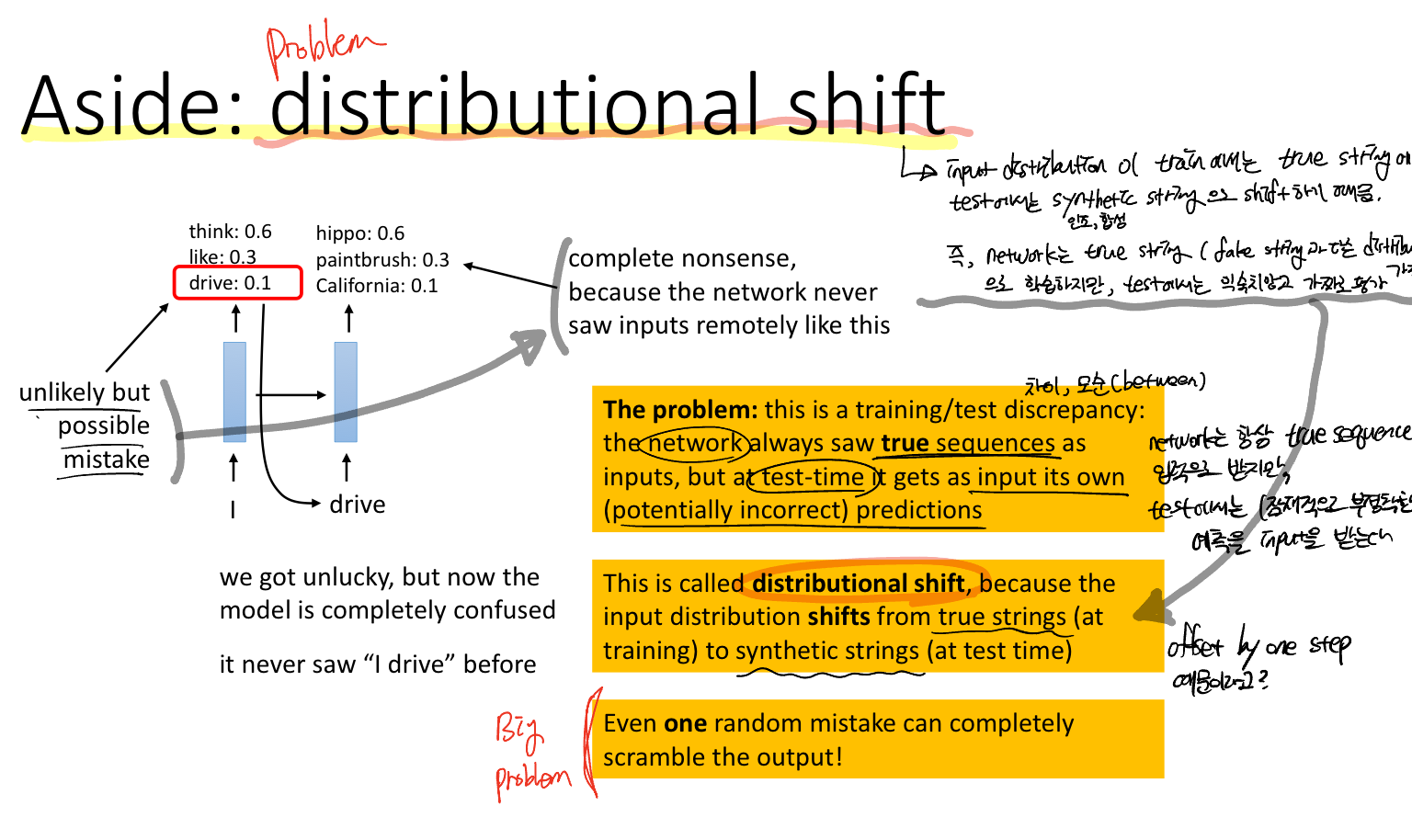
Problem: distributional shift, train과 test 간의 discrepancy

이 문제는 모델이 데이터의 실제 시퀀스에 대해 학습하는데, 테스트 데이터는 학습한 적이 없는 데이터이기 때문에 부정확한 예측을 한다는 것입니다. 또한, 이전 페이지에서 말했듯이 연속적인 데이터 사이의 조건부 확률이기 때문에 한번의 실수가 연쇄적인 오류를 발생시킨다는 문제가 발생한다는 것입니다.

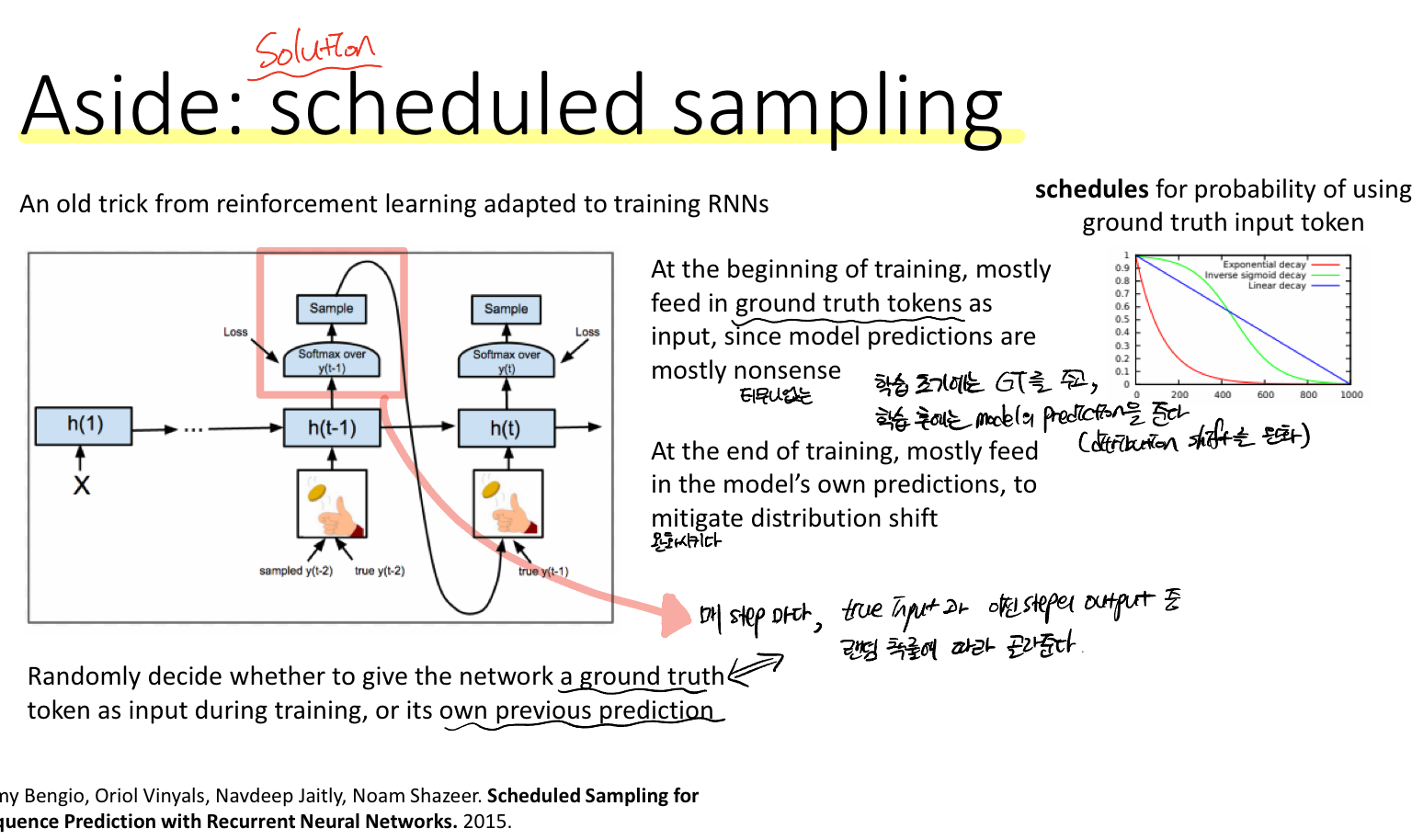
Solution: Scheduled sampling

훈련 중에는 네트워크에 때로는 실측 데이터(시퀀스의 실제 다음 토큰)을 입력으로 주어주는 것을 말한다. 학습 후에는 점차 모델의 prediction을 주어줌으로써 distribution shift 문제를 완화하는 효과를 보여준다.

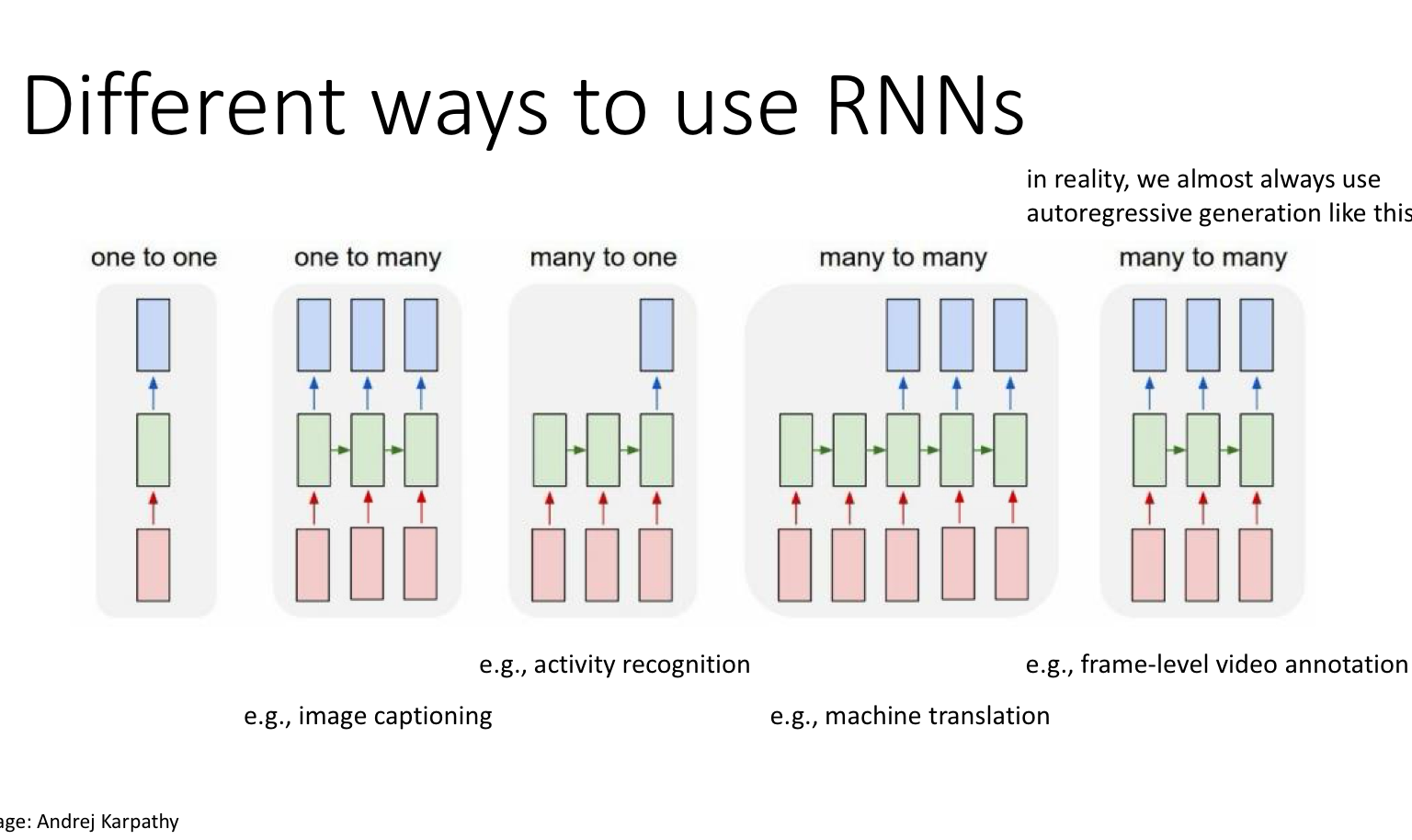
각 task에 맞게 RNN 모델을 다양하게 사용할 수 있다.

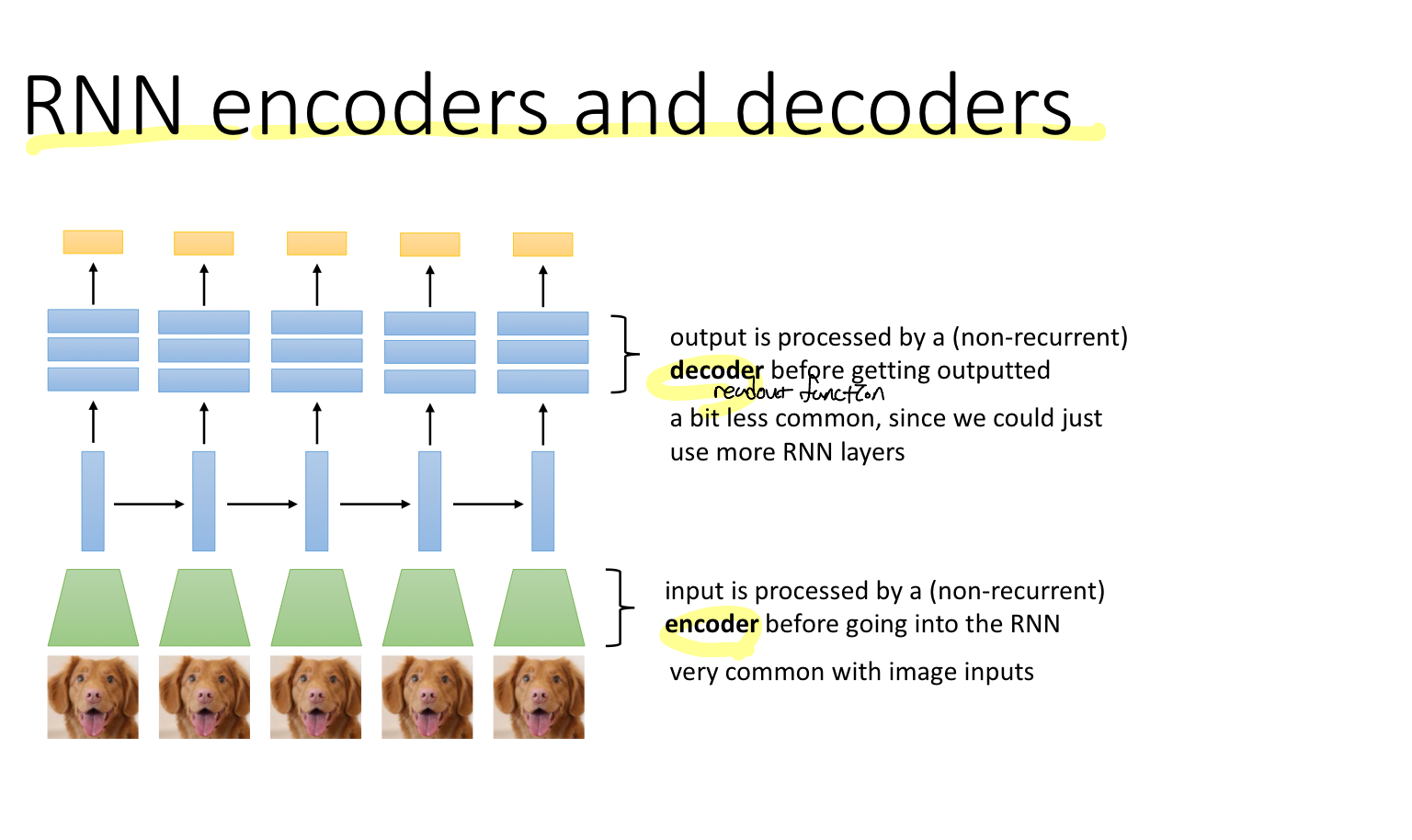
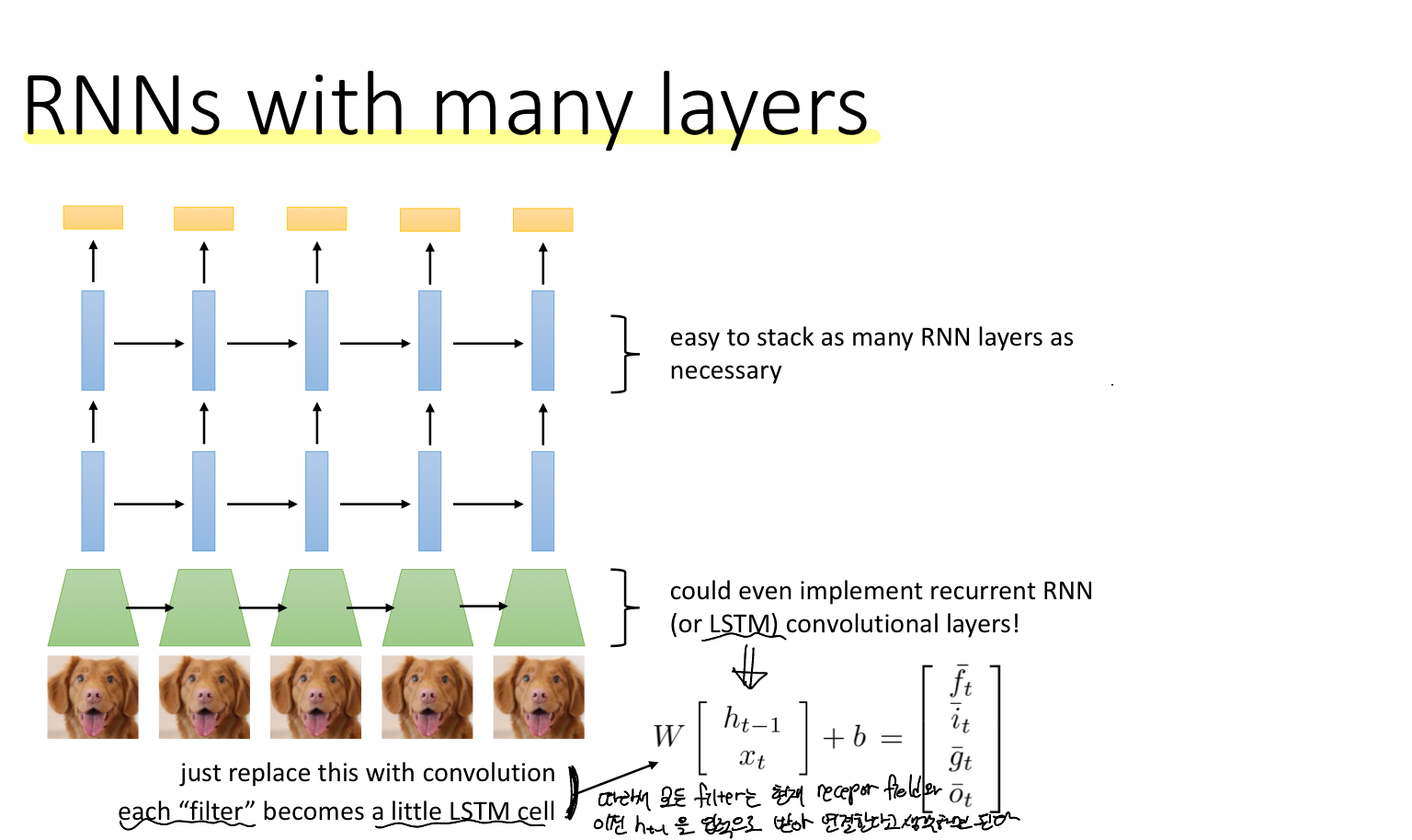
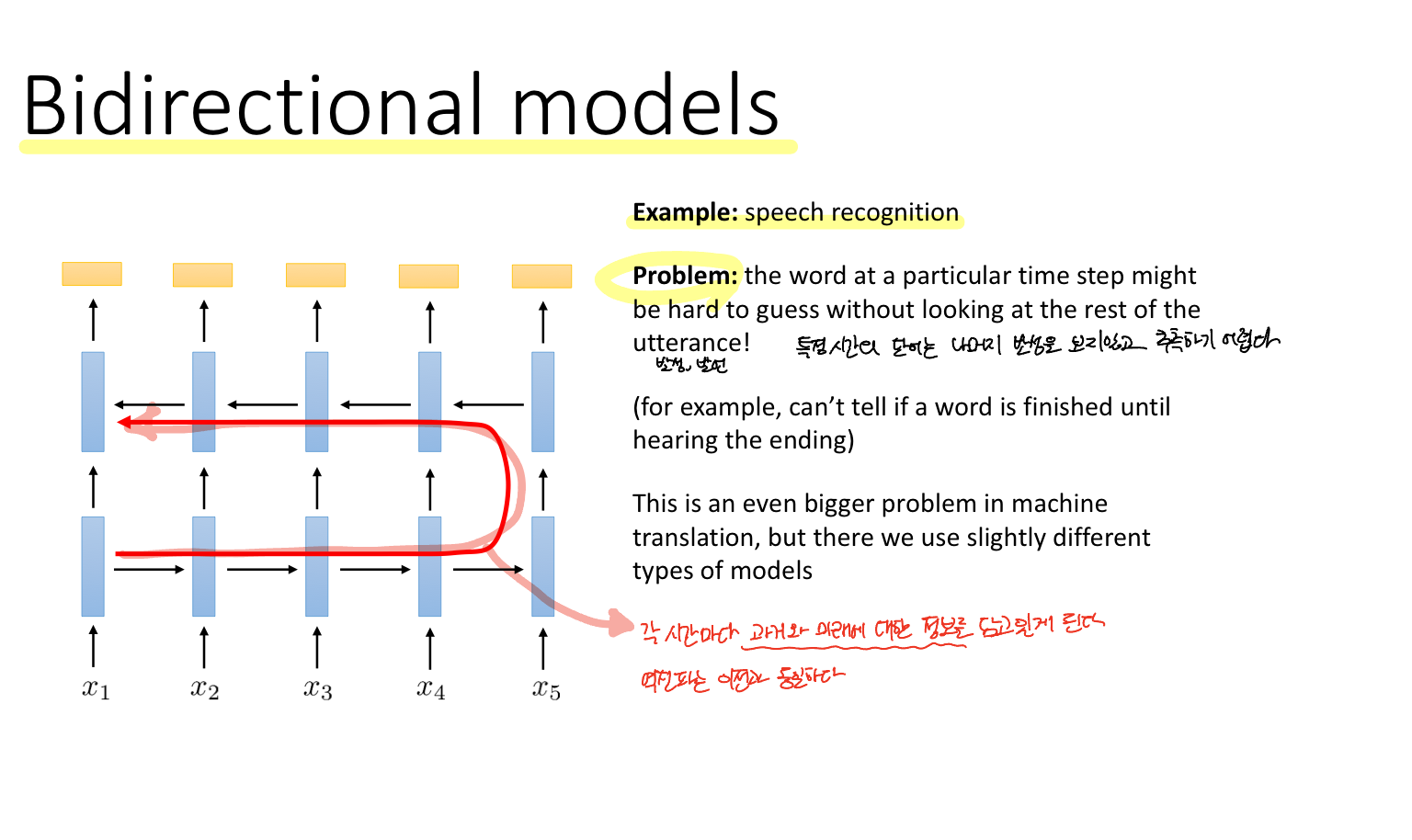
RNN은 1) 각 레이어마다 입력과 출력을 갖는 네트워크이며 2) 모든 레이어에 대해서 가중치를 공유

하지만 RNN은 vanishing/exploding gradient 문제가 있다. 이 문제를 해결하기 위한 모델로는 LSTM, GRU 등이 있다.

RNN이 매 스텝마다 입력과 출력을 갖는 이유는 structured prediction을 위해서 이다.