
이번 강의는 머신러닝의 기초에 대한 내용입니다.

이번 강의에서는 지도학습에 대해서만 다룬다. 입력 x를 넣으면 y가 나오는 함수를 생각하면 된다. 이때 y가 나오도록 하는 함수 f의 계수를 우리는 학습하는 것이다.

지도학습을 예로 들자면, 이미지가 입력이면 대상의 카테고리가 출력. 영어 문장이 입력이면 프랑스어 문장이 출력. 이렇듯 이산적인 형태를 띄고 있다.


이산적인 레이블은 예측하기 더 쉽다. 부드럽기 때문에 학습하기도 쉬운데, 직관적으로 불연속적인(이산적)인 레이블을 확률로 표현을 하면 연속적인 레이블로 표현할 수 있다.

본 내용에 앞서 알아둬야 할 것이 체인룰과 조건부 확률.
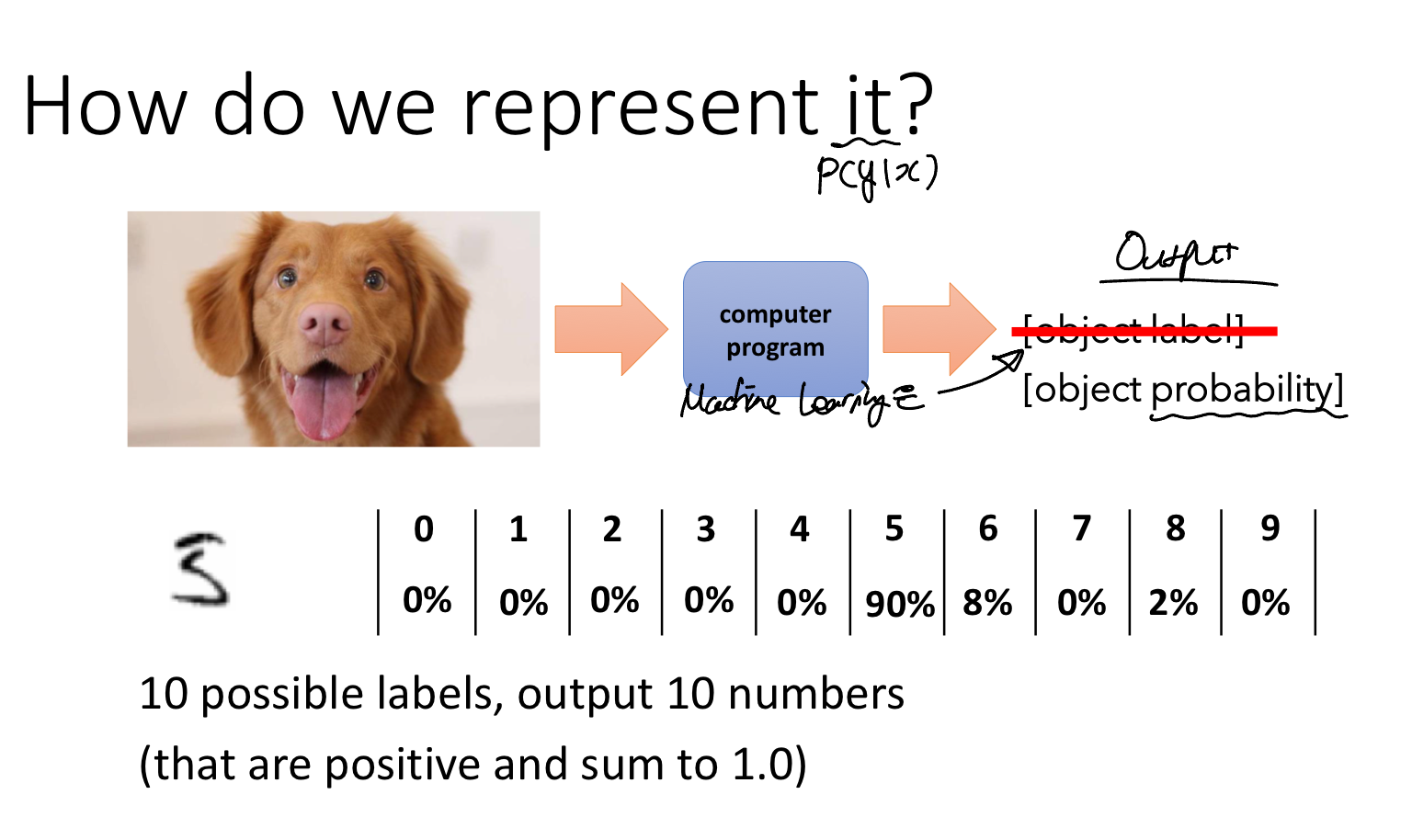
Q. 조건부 확률을 어떻게 표현할 것인가?
이제 우리는 레이블을 출력하는 것이 아니라, 확률을 출력하는 것이다. 그렇다면 확률이란 무엇일까? 확률의 특징은 항상 양수이며, 동시에 총합은 1이어야 한다는 것이다.
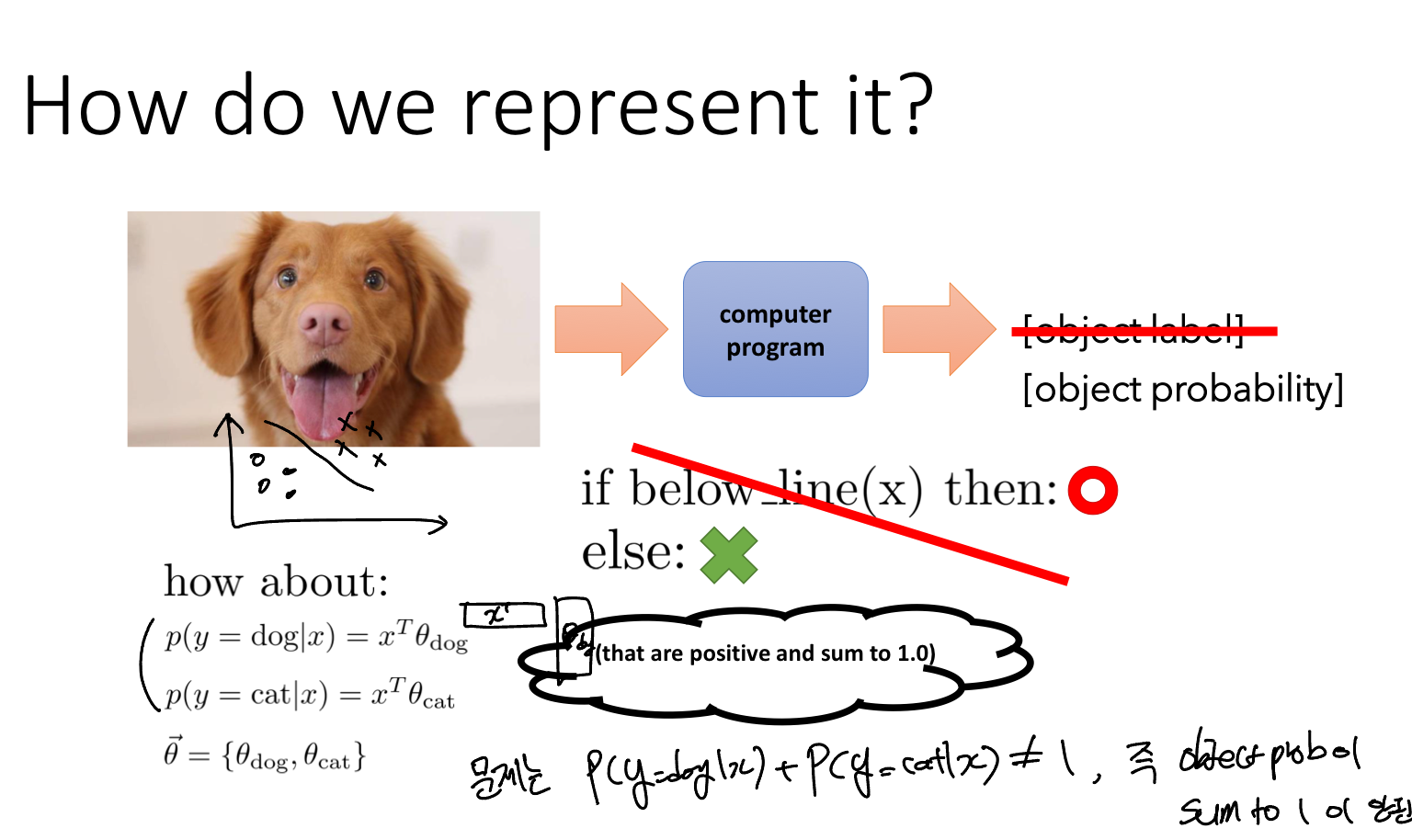
입력 데이터가 주어졌을 때, 출력이 개 혹은 고양이일 확률을 표현하는 것을 생각해보자. 근데 개일 확률과 고양이일 확률의 합은 1이 아니다. 그 이유는 소일수도, 코끼리일수도, 악어일수도 있기 때문이다. 무슨 말이나면, 모든 경우의 수가 될 확률을 구해 합해야지 1이 된다는 말이다.
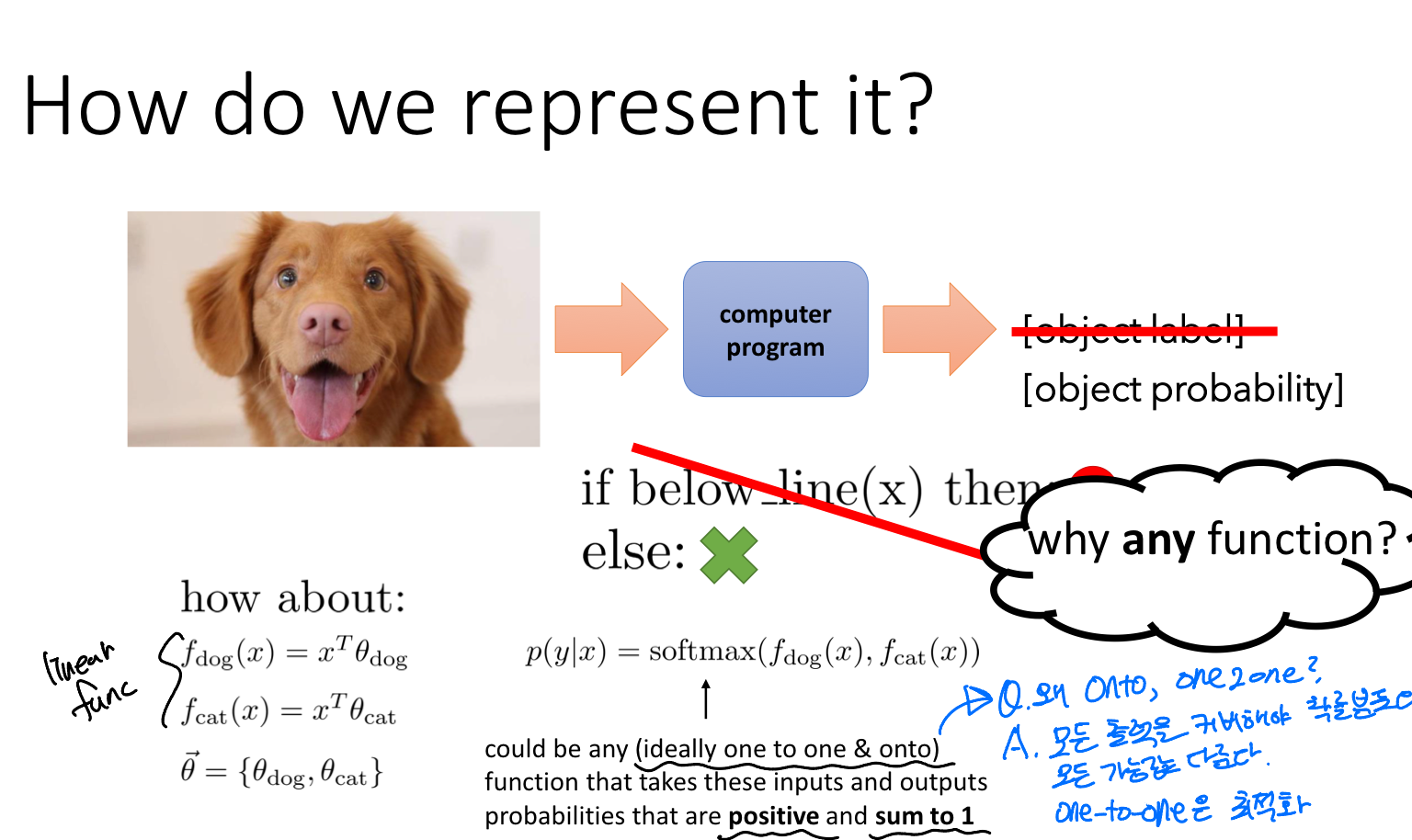
그럼 어떻게 Positive and sum to 1.0을 만족할 수 있을까? 이를 위해서는 One to One & Onto에 대해서 알아야한다.
먼저 One to One은 일대일 함수로, 치역이 하나의 정의역에만 대응되는 경우를 말한다. Onto는 전사 함수로, 공역과 치역이 같은 함수를 말한다. 이것이 왜 알아야할까?
이전 페이지에서 말했듯이, 모든 경우의 출력을 커버해야 확률분포의 모든 가능값을 다룰 수 있기 때문이다. 즉, 개나 고양이, 토끼, 코끼리 등 모든 가능값을 커버할 수 있어야지 확률을 구할 수 있다.

그래서 다시 본론으로 조건부 확률을 어떻게 표현할 수 있을까?
첫 번째, 어떻게 Positive number를 만들 수 있을까? 제곱근 / 절대값 / maximum함수 / exponential(지수함수) 등이 있다. 우리는 지수함수를 선택하지만, 어떤 것을 선택해도 문제는 없다.
두 번째, 어떻게 Sum to 1을 만들 수 있을까? 단순하다. 모든 경우의 수를 다 더하면 된다.

위의 조건을 다 합한 것이 softmax 함수이다.
ㅇ
ㅇ
ㅇ
ㅇ
ㅇ
ㅇ
ㅇ
ㅇ
ㅇ
ㅇ
