CS 285 Online Course at UC Berkeley의 Assingment2에 대한 내용입니다.
1. Reward-to-go
Discrete 환경 (CartPole-v0)에서 PG algorithms이 동작할 때 Batch_size의 크기, Advantage standardization, reward-to-go가 모델에 성능에 미치는 영향에 대해 분석해보는 것이 목표이다.
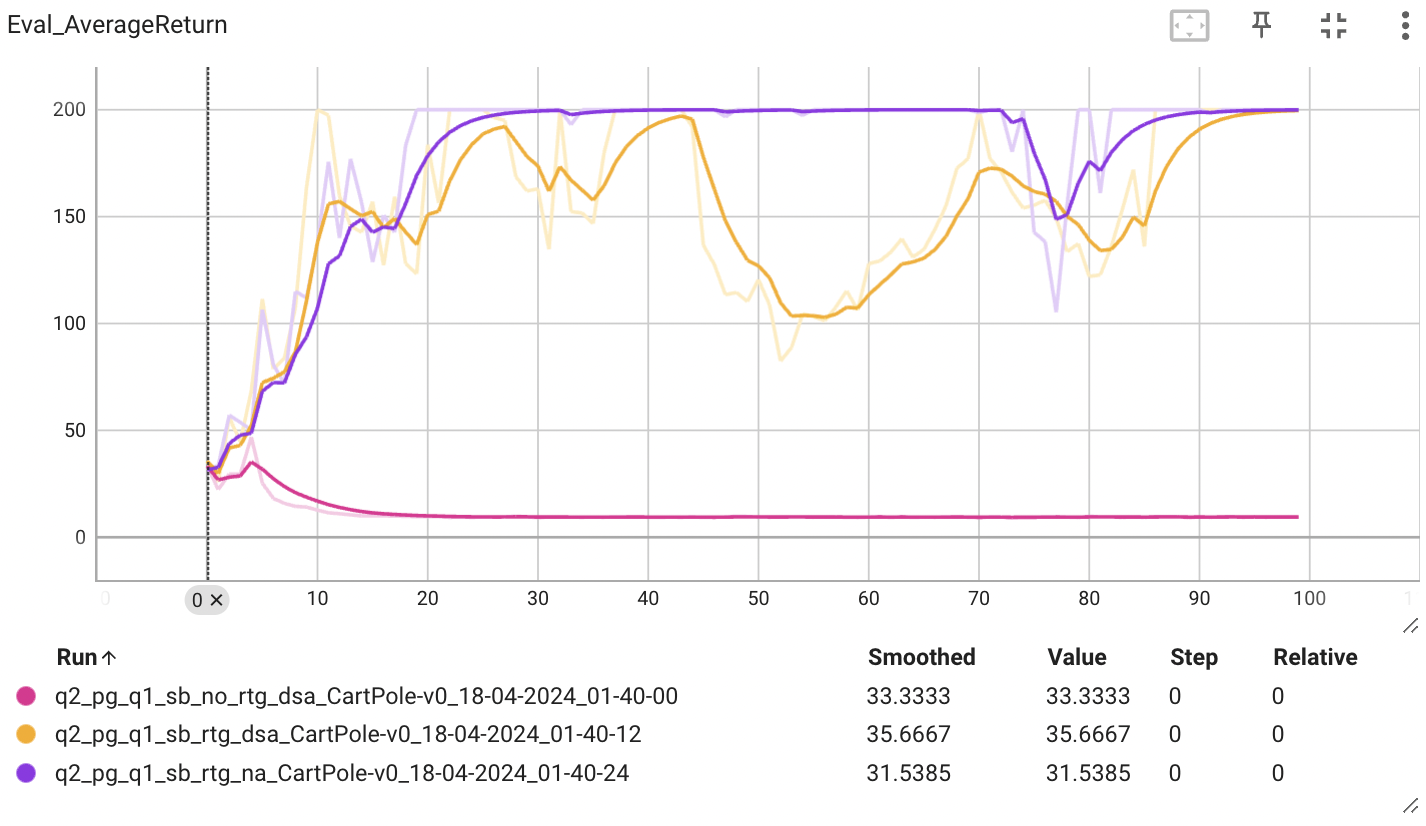
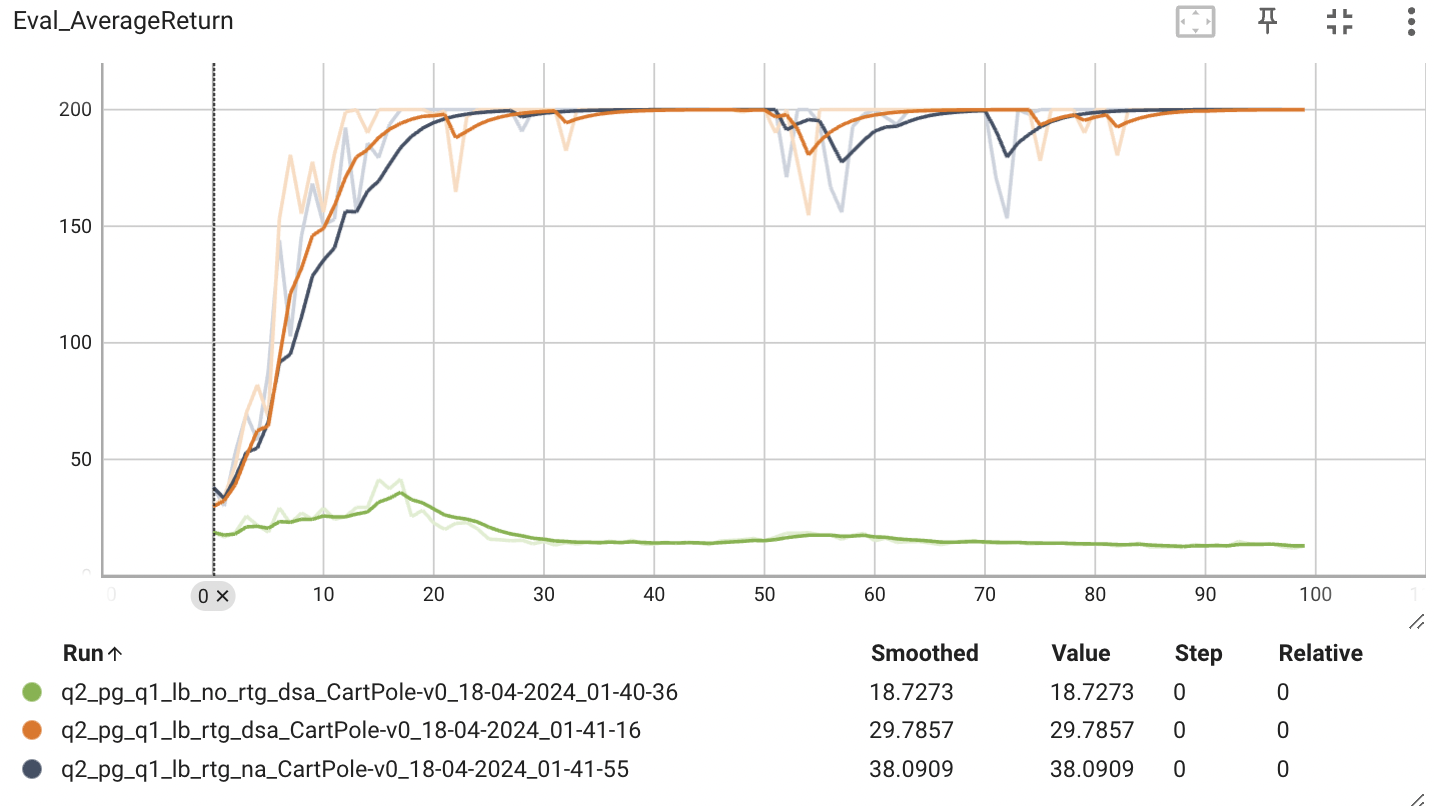
Which value estimator has better performance without advantage-standardization: the trajectory- centric one, or the one using reward-to-go?
Advantage-standardization을 적용하지 않았을 때, reward-to-go를 사용한 추정기의 성능이 월등히 높은 것을 알 수 있다. reward-to-go는 action과 reward 사이의 causality 인과관계를 고려한 개념이다. 앞으로 얻을 모든 보상을 고려하는 것이 아니라, 에이전트가 현재 시점부터 미래에 얻을 보상에만 기반하여 정책을 업데이트하는 것입니다. 비슷한 개념이 Markov property가 있다. 마르코프 성질은 미래의 상태는 과거와 dependent하다는 것이다.
정리하면 Reward-to-go를 사용하면, 에이전트가 고려하는 리턴의 길이가 감소하고, 각 시간 단계에서의 리턴의 분산도 감소한다. 또한, 에이전트가 각 시간 단계에서 독립적인 리턴을 기반으로 결정을 내릴 수 있게 함으로써 상관관계를 감소시켜 리턴의 총 분산이 감소하게 됩니다. 이를 수학적으로 증명해보자.
먼저, 리턴의 길이 감소하면 분산이 감소하는 것에 대해 알아보자. 에피소드에서 t이후 누적 보상인 리턴을
으로 나타낸다. 이때 리턴의 분산은 각각의 보상 r들의 분산과 이들 간의 공분산 합으로 계산된다.
따라서 에피소드의 길이 T가 줄어들면, 항의 개수가 줄어들고, 공분산 항 도 개수가 줄어들어 전체적인 분산이 감소하게 된다.
다음으로 상관관계 감소에 따른 분산의 감소에 대해 알아보자. 상관관계, 즉 공분산은 두 확률 변수의 관계의 강도를 측정한다. 공분산은 다음과 같이 정의된다.
이때 이 값이 0에 가까워지면, 변수들 사이에 선형 관계가 적다는 것을 의미하며, 이는 변수들(X와 Y)이 독립적이라는 것을 의미한다. 공분산이 0이 되면, 두 변수의 분산을 단순히 합산하여 전체 분산을 구할 수 있다.
공분산이 0일 경우,
으로 간소화된다. 즉, 두 변수가 독립적일 때, 두 변수의 합의 분산은 각 변수의 분산의 합과 같다. 따라서 상관관계가 감소하면(공분산이 줄어들면) 전체 보상의 분산이 감소한다.
아래의 코드는 r.t.g를 적용하지 않을 때 reward 총합과 적용했을 때 총합을 구하는 함수를 구현한 코드이다. reward의 분산을 줄이는 또 다른 방법인 discount_factor 가 곱해져있는 걸 볼 수 있다. 즉, 현재 시점과 먼 시간의 reward는 영향이 적다는 것을 반영한 것이다.
def _discounted_return(self, rewards):
list_of_discounted_returns = []
accumulated_return = 0
power_of_gamma = 1 # gamma^0 is 1
for reward in rewards:
accumulated_return += power_of_gamma * reward
list_of_discounted_returns.append(accumulated_return)
power_of_gamma *= self.gamma # gamma^t, update gamma to the next power for next iteration
return list_of_discounted_returns
def _discounted_cumsum(self, rewards):
n = len(rewards)
list_of_discounted_cumsums = [0] * n
cumulative_sum = 0
for t in reversed(range(n)):
cumulative_sum = rewards[t] + self.gamma * cumulative_sum
list_of_discounted_cumsums[t] = cumulative_sum
return list_of_discounted_cumsumsDid advantage standardization help?
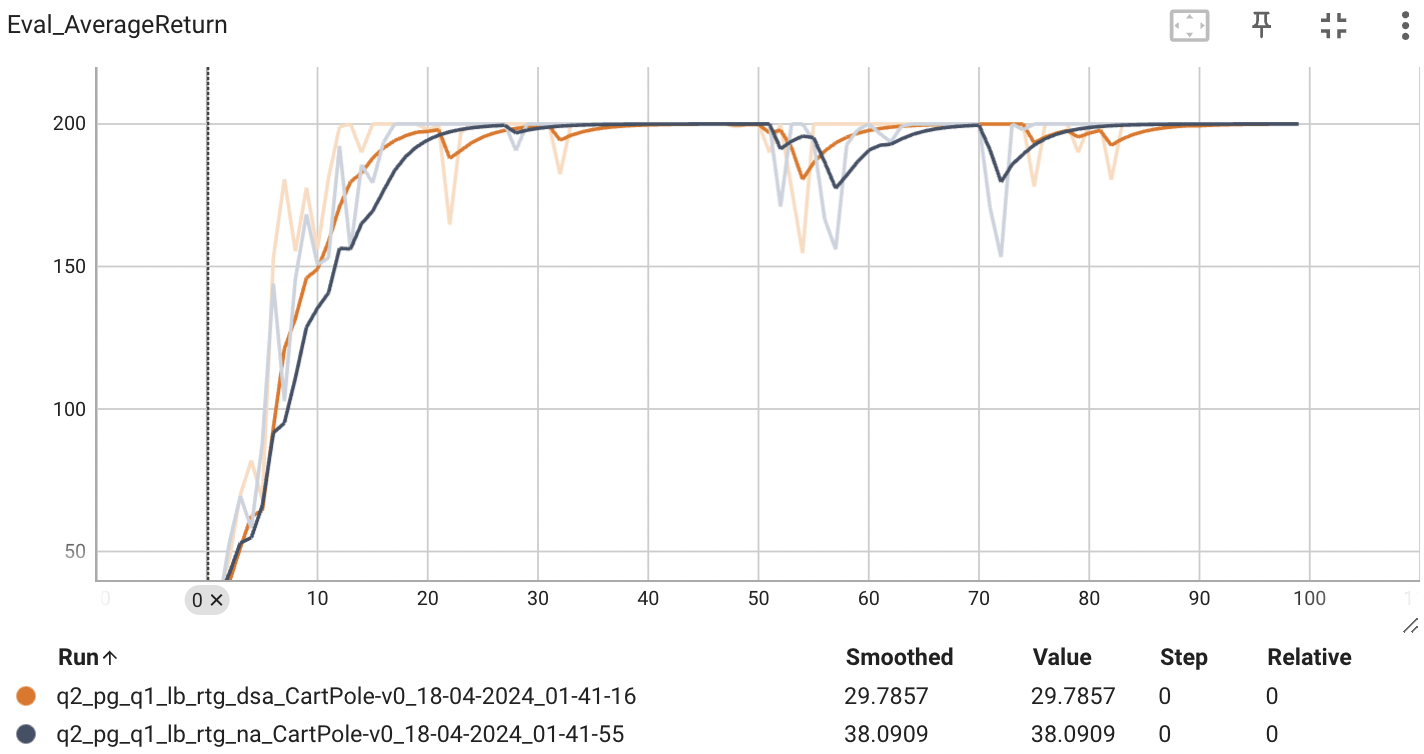
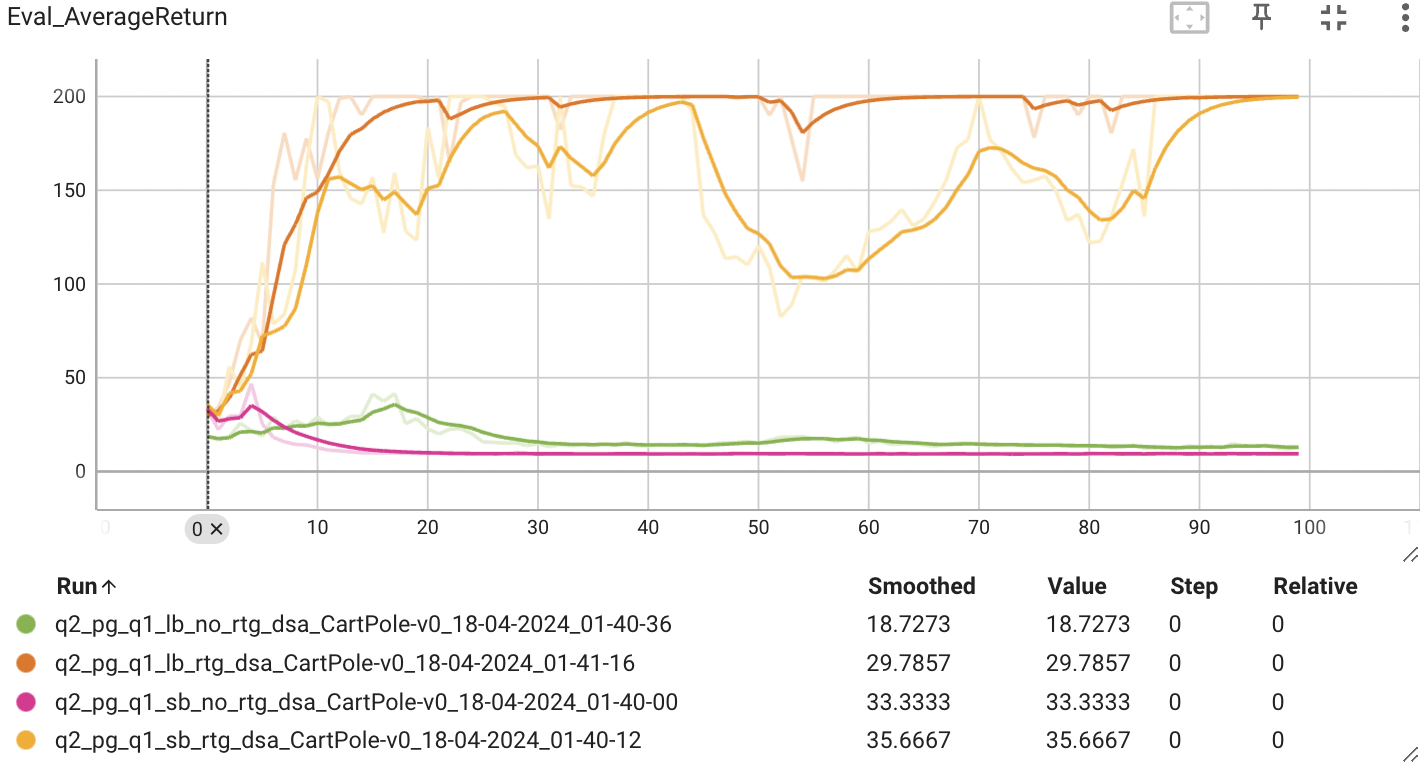
배치 사이즈가 작을 때는 advantage-stadardization을 적용했한 estimator의 성능이 더 높은 것을 확인할 수 있다. 반면, 배치 사이즈가 클 때는 큰 차이가 있지 않았다. 왜 그럴까?
먼저 Advantage에 대해서 알아보자. Advantage는 reward의 변형이라고 볼 수 있는데, 결국 현재 state에서 취한 action이 얼마나 좋은가를 나타내는 지표라고 볼 수 있다. 이 실험에서는 Advantage는 곧 r.t.g가 적용된 reward이다. 이때 reward의 총 합을 Q-function 라고 정의하면 policy gradient는 다음과 같이 정리할 수 있다.
이때는 가 advantage가 된다.
즉 advantage는 gradient의 input으로 들어가는 변수이다. 따라서 Backpropagation 과정에서 advantage는 gradient에 영향을 미치게 된다. 왜냐하면 "gradient will get scaled by big x values"이기 때문이다. 이는 이전에 수강했던 "CS182 UC Berkely Lecture7 - Getting Neural Nets to Train"에서 확인할 수 있다. 아래 사진은 해당 부분의 강의 노트이다.
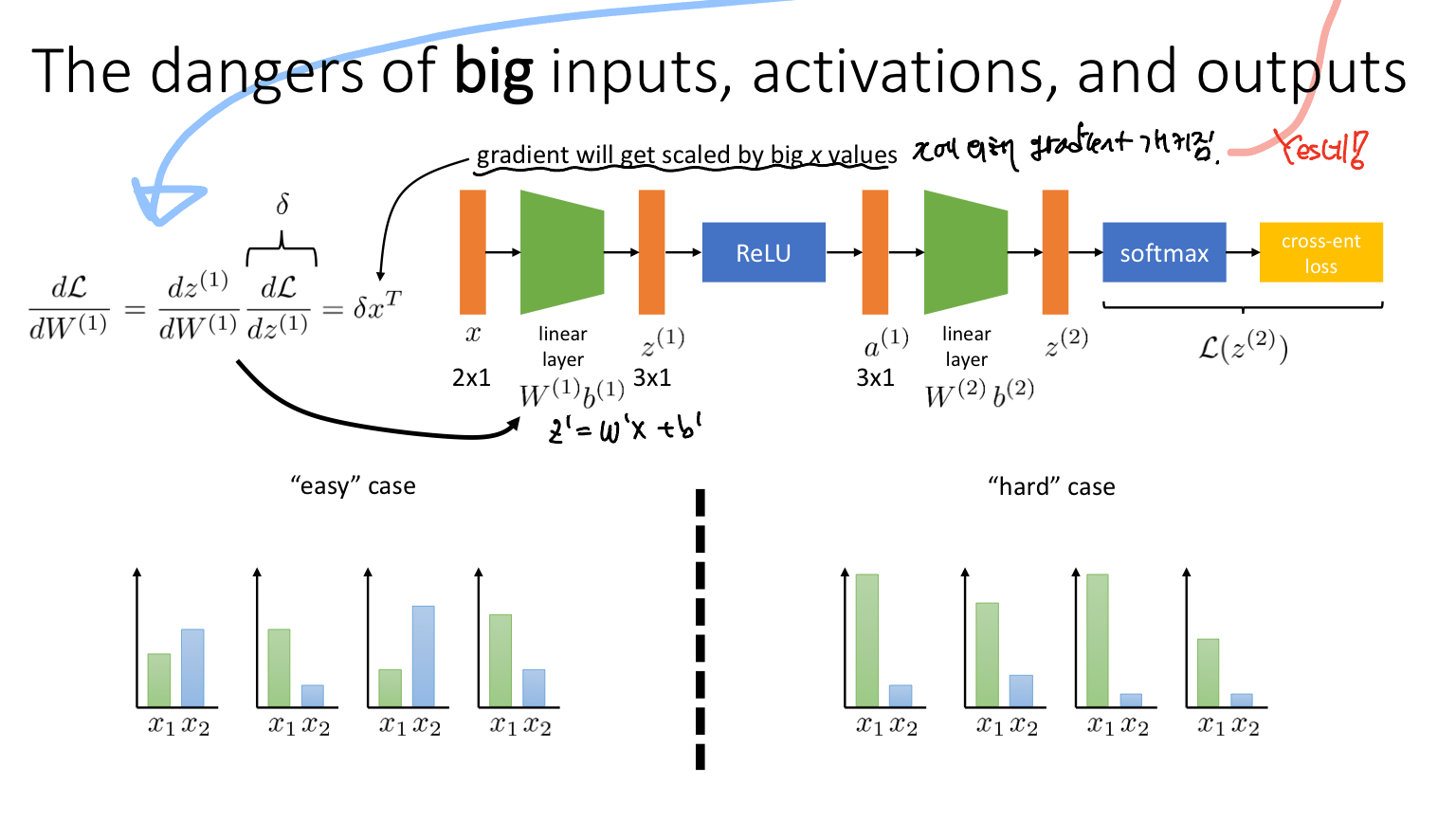
정리하면, advantage-standarization은 보상의 스케일을 조정하는 표준화를 통해 학습을 안정화시키고 가속화하는 데 도움을 준다.
다시 배치 사이즈의 크기가 다른 두 그래프를 보면, 배치 사이즈가 작을 때는 advantage-standarization의 효과가 나타나지만 배치 사이즈가 클 때는 advantage-standarization의 효과가 성능에 큰 영향을 미치지 않는다. 왜 이런 결과가 나올까?
큰 배치 사이즈는 이미 각 추정치의 분산을 줄여주기 때문이다. 즉, 다양한 경험을 통해 보상의 분포를 보다 잘 근사화할 수 있게 함으로써 개별 보상의 outlier가 전체 평균에 미치는 영향이 줄어들어 advantage-standarization의 효과가 상대적으로 감소하는 것으로 보인다.
반면, 배치 사이즈가 작을 때는 각 배치 샘플이 전체 분포를 충분히 대표하기 어렵다. 따라서 advantage-standarization을 적용하면 보상의 relative importance를 더 잘 이해하게 된다. 결과적으로, 에이전트가 더 안정적으로 좋은 정책을 학습하도록 도와주어 더 높은 성능으로 이어진다.
정리하면, advantage-standarization은 배치 사이즈가 작아 데이터의 분산이 큰 경우에 효과적이며, 작은 배치 내에서 보상의 scale을 조정하여 효과적으로 학습하기 때문이다.
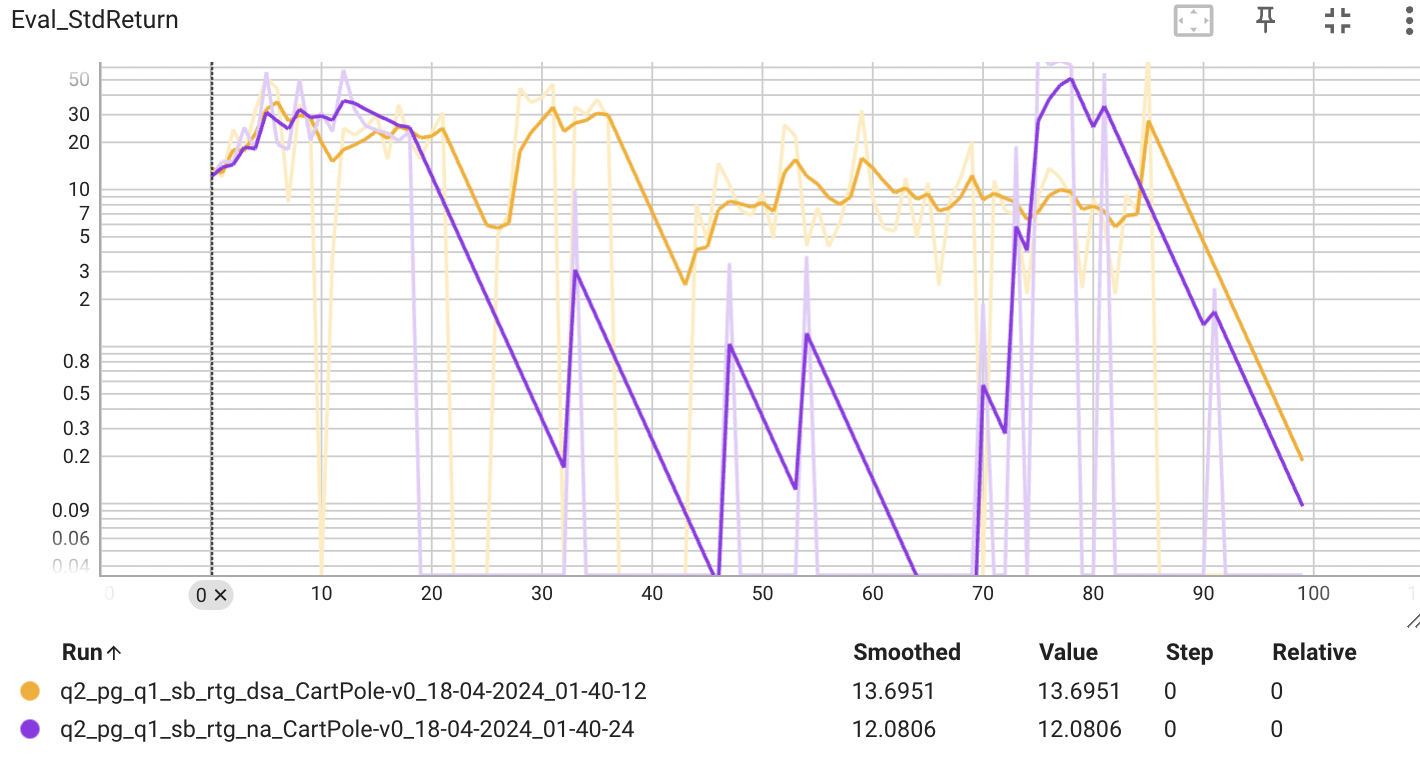
위의 그래프는 배치 사이즈가 작은 경우, 보상의 표준편차를 나타낸다. 표준편차가 낮다면, estimator의 성능이 다양한 에피소드에서 일관된 성능을 보이고 있다는 의미로 볼 수 있다. 그래프에서 볼 수 있듯이 advantage-standarization을 적용했을 때 낮은 표준편차를 보이는 것을 확인할 수 있다.
Did the batch size make an impact?
배치 사이즈는 학습에 사용되는 데이터의 크기를 뜻한다고 하면, 배치 사이즈가 클수록 더 많은 데이터에 대해 학습이 이루어지기 때문에 더 높은 성능을 보일 것이라 예상할 수 있다.
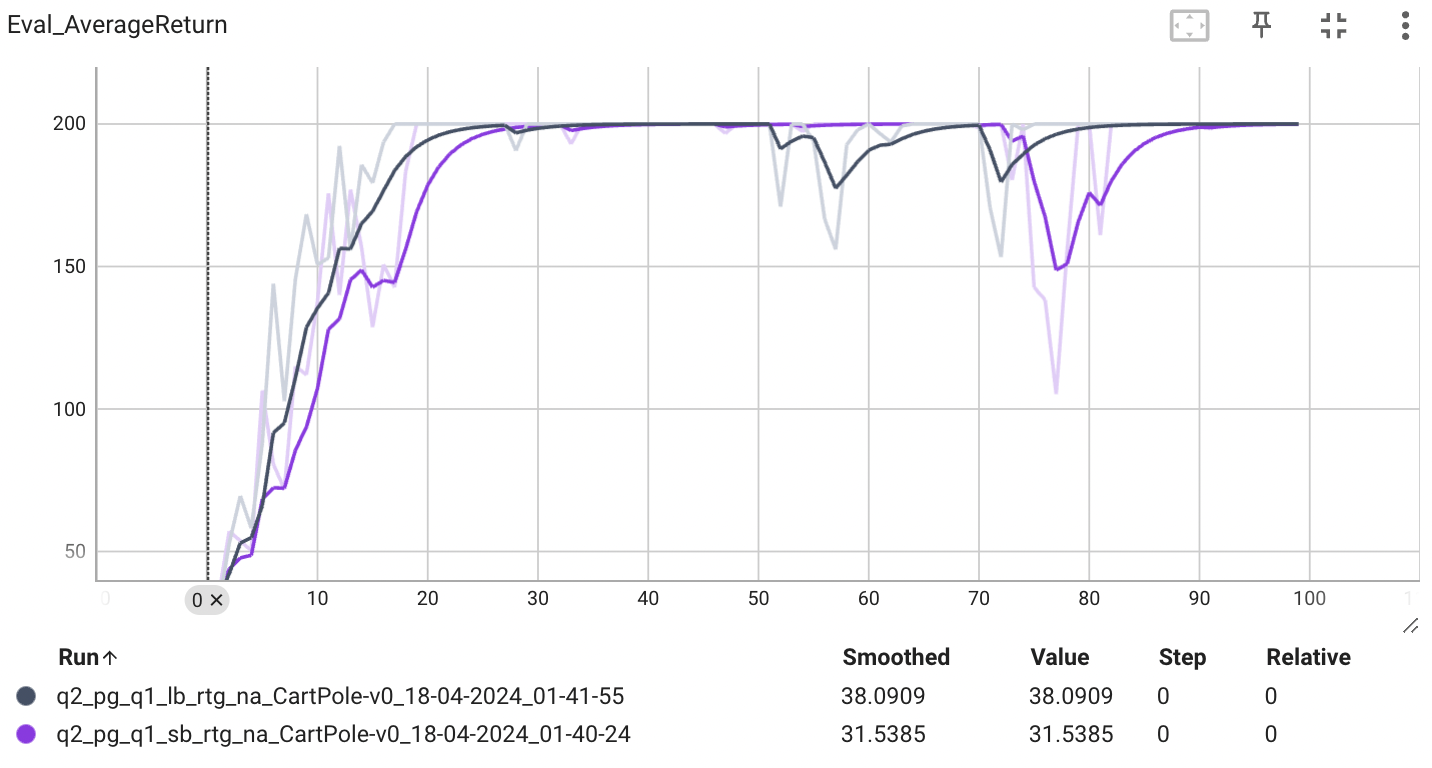
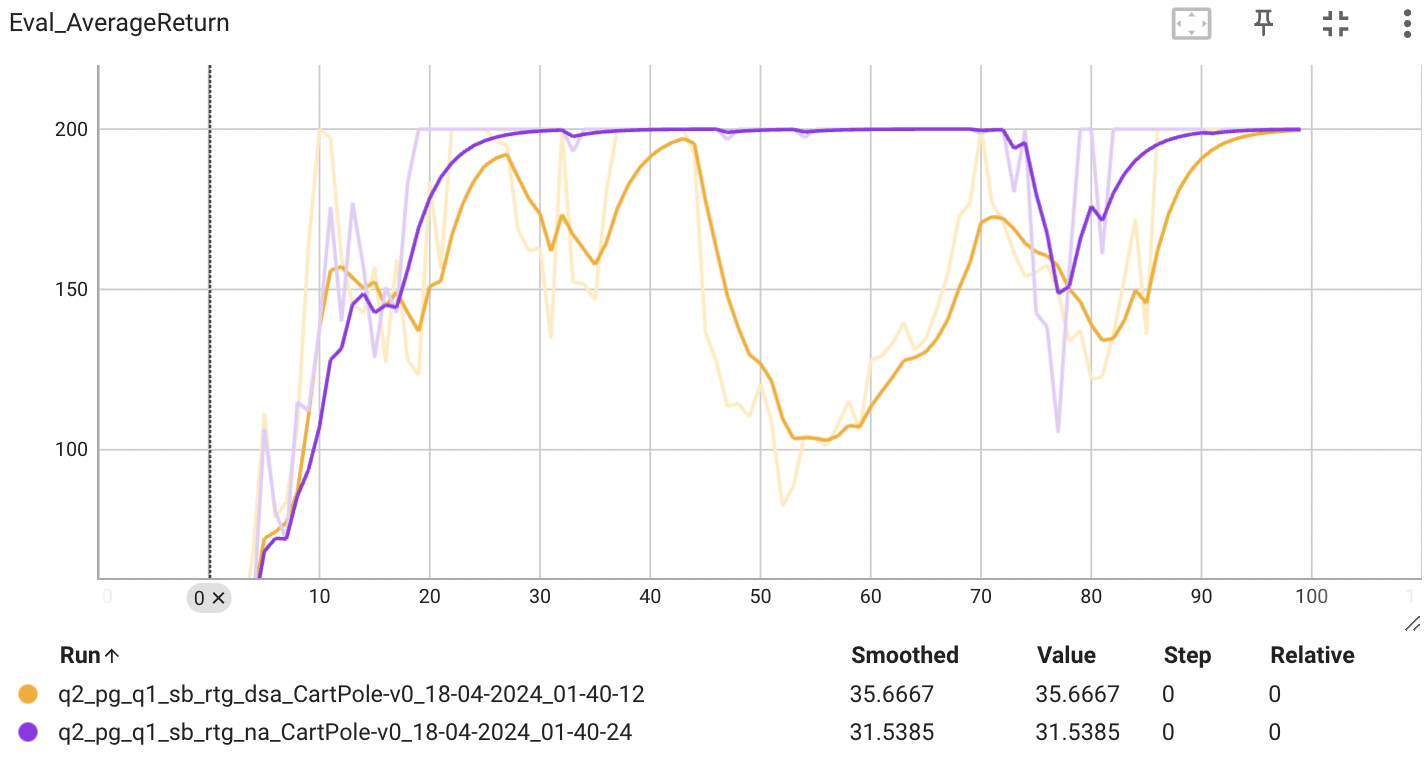
위의 그래프는 r.t.g와 advantage-standarization을 적용했을 때 배치 사이즈의 크기에 따른 estimator의 성능을 비교할 수 있다. 큰 배치 사이즈를 사용했을 때 더 빠르고 안정적인 성능을 보이는 것을 알 수 있다.
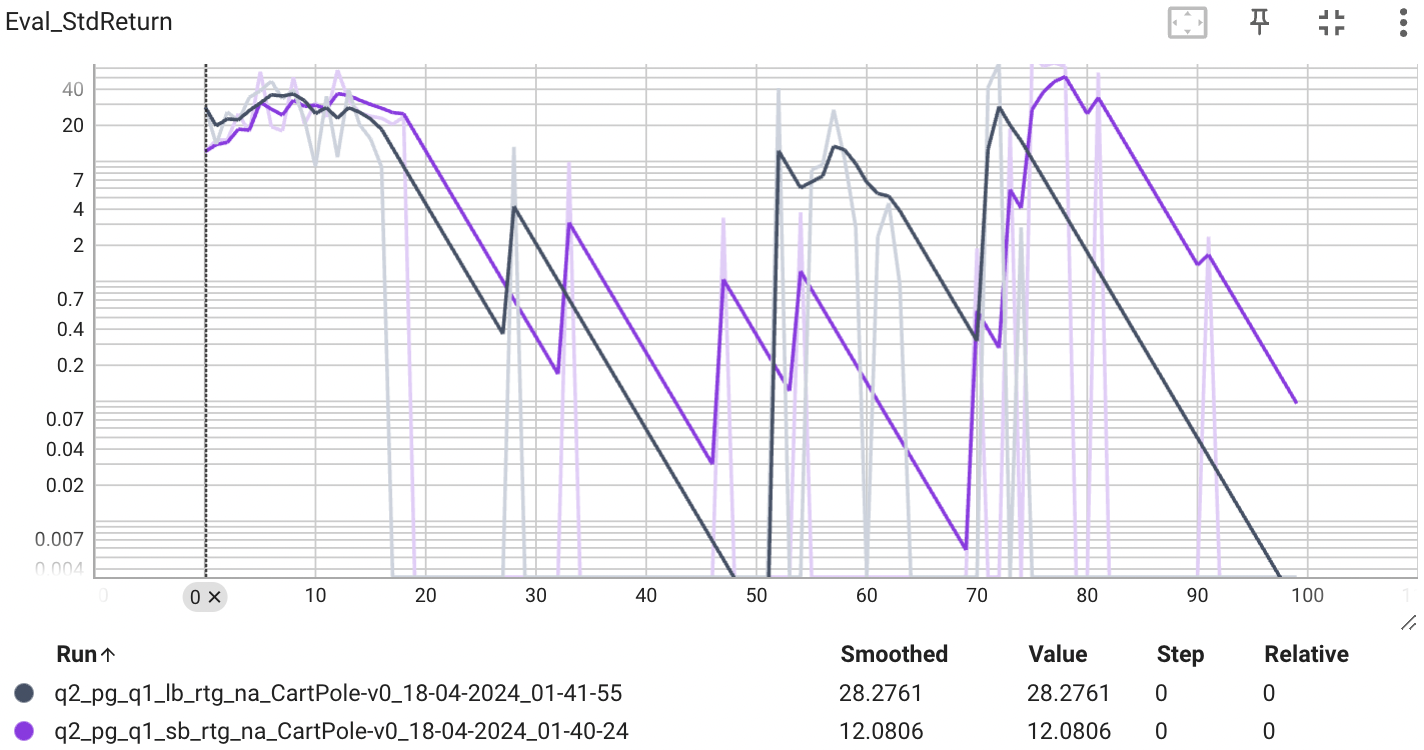
표준편차를 확인해보아도 큰 배치 사이즈인 경우가 더 낮은 표준편차를 보이는 것으로 보아, 큰 배치 사이즈는 분산을 낮추는 효과를 보이는 것을 알 수 있다.
