Policy Gradients_Neural Network Baselines_[CS285_HW2]

Eony_Jahng·2024년 4월 24일

CS285

목록 보기

2/4

CS 285 Online Course at UC Berkeley의 Assingment2에 대한 내용입니다.

이번에는 reward-to-go 이외에 variance를 줄일 수 있는 또 다른 방법인 Baseline에 대해 알아보려 한다.

\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \log p_{\theta}(\tau) r(\tau)

policy gradient는 좋은 trajectory에 대해서는 높은 reward, 나쁜 trajectory에 대해서는 낮은 reward가 주어진다면 policy는 결국 높은 reward를 갖는 최적의 policy를 찾아갈 것이다.

하지만 만약 모든 reward가 양수라면 어떻게 될까? 모든 trajectory에 대해 끝없이 커질 것이다. 이 문제를 해결하기 위해서 reward의 부호와 관계없는 어떤 기준이 필요하다. 즉 보상의 정규화가 필요하다. 그것이 baseline이라 명하고 reward의 평균이 된다.

b = \frac{1}{N}\sum_{i=1}^N r(\tau)

또한, 이전에 reward-to-go를 $\hat{Q}_{i,t}$ 로 표현했었다. 이는 하지만 MDP를 따르는 여러 가능성 중 하나에 불구하다. 즉, 어떤 시점 t에서 (state, action)이 주어졌을 때의 Q값을 의미한다. 이를 명확하게 표현하면 현재 상태와 액션이 주어졌을 때 Q값이 참 값이 된다.

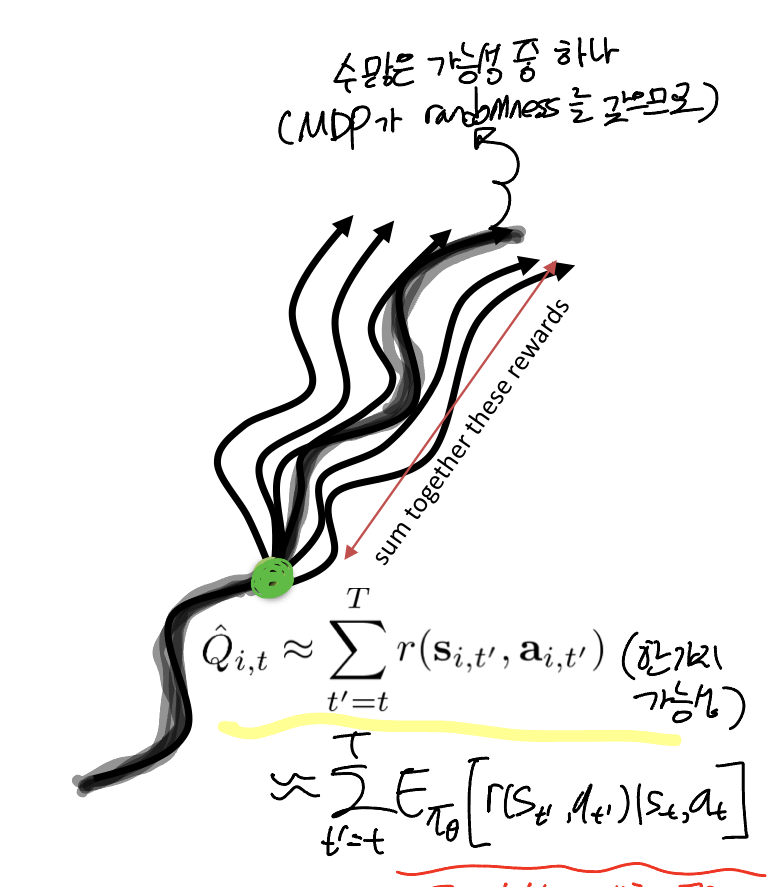
Q(s_t, a_t) = \sum^T_{t'=t} \mathbb{E}_{\pi_\theta}[r(s_{t'},a_{t'})|s_t,a_t] : true\ expected \ r.tg \\ : total \ reward\ from\ taking\ a_t\ in\ s_t

그렇다면 보상의 평균인 baseline은 무엇일까? Q값의 평균이 되어야 한다. 즉, 현재 상태에서 선택할 수 있는 모든 action에 대한 기댓값(평균값)이 되어야 한다. 그리고 이것을 Value function이라 정의한다.

V(s_t) = \mathbb{E}_{a_t\sim\pi_\theta(a_t|s_t)}[Q(s_t,a_t)] \\ : total\ reward\ from\ s_t

Q는 주어진 상태에서 특정 액션을 행했을 때 total reward, V는 주어진 상태에서 total reward. 그럼 Q에서 V를 빼면 현재 상태에서 특정 액션이 가능한 모든 액션에 비해 얼마나 좋은가를 나타내는 식이 된다. 그리고 이것을 Advantage function이라 정의한다.

A(s_t,a_t)=Q(s_t,a_t)-V(s_t)

마지막으로 Q, V, A는 모두 현재 policy에서 sampling된 state와 action를 따르기 때문에 다음과 같이 정의한다.

Q^\pi(s_t, a_t) = \sum^T_{t'=t} \mathbb{E}_{\pi_\theta}[r(s_{t'},a_{t'})|s_t,a_t]

V^\pi(s_t) = \mathbb{E}_{a_t\sim\pi_\theta(a_t|s_t)}[Q(s_t,a_t)]

A^\pi(s_t,a_t)=Q^\pi(s_t,a_t)-V^\pi(s_t)

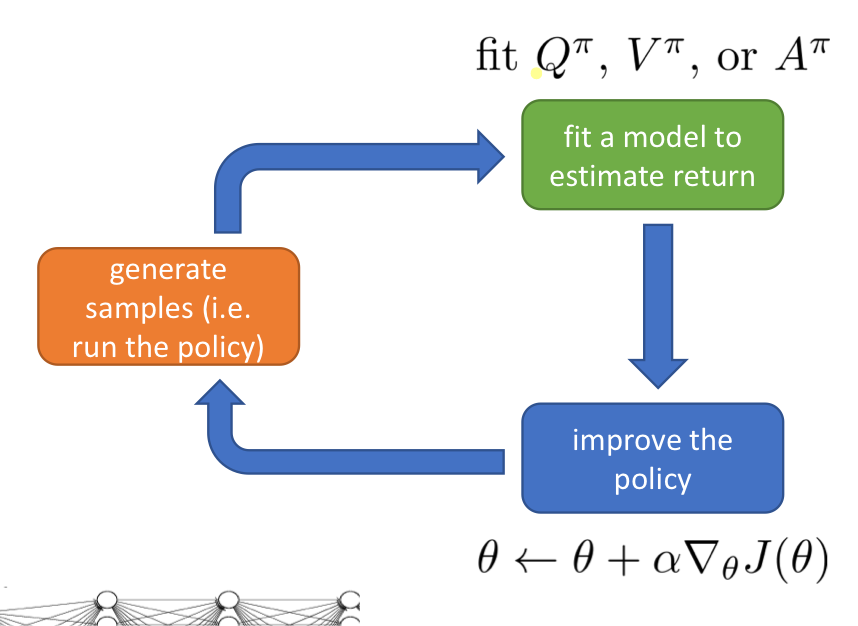
위는 알고리즘 프로세스입니다. Q, V, A 중 어떤 것을 fitting 해야 할까? Q함수를 다시 살펴보자.

\begin{aligned} Q^\pi(s_t, a_t) &= \sum^T_{t'=t}\mathbb{E}_{\pi_\theta}[r(s_{t'},a_{t'})|s_t,a_t]\\ &= r(s_t,a_t)+\sum^T_{t'=t+1}\mathbb{E}_{\pi_\theta}[r(s_{t'},a_{t'})|s_t,a_t]\\ &=r(s_t,a_t) + V^{\pi}(s_{t+1})\\ &=r(s_t,a_t)+\mathbb{E}_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}[V^\pi(s_{t+1})]\\ &\approx r(s_t,a_t)+V^\pi(s_{t+1}) \end{aligned}

식을 살펴보면, 현재 받는 즉각적인 보상과 그 다음 시간부터 받을 수 있는 보상의 기댓값으로 나뉘는 걸 알 수 있습니다. 이때 사용되는 개념이 벨만 기대 방정식 Bellman Expectation Equation입니다.

벨만 기대 방정식 Bellman Expectation Equation

벨만 기대 방정식(Bellman Expectation Equation)은 강화 학습에서 사용하는 중요한 개념으로, 정책 𝜋를 따를 때 각 상태의 가치를 평가하는 방정식입니다. 이 방정식은 각 상태의 가치가 그 상태에서 받을 수 있는 즉각적인 보상과 미래 상태들의 가치의 합계라는 점을 기반으로 합니다.

벨만 기대 방정식은 다음과 같이 표현됩니다:

V^\pi(s) = \mathbb{E_{\pi}}[R_{t+1}+\gamma V^\pi(s_{t+1})|s_t=s]

위의 과정에서 벨만 기대 방정식은 세 번째 단계에서 사용됩니다. 현재 상태에서 받는 즉각적인 보상에다가, 그 다음 상태에 대한 가치의 기대값을 더합니다. 이때, 기대값은 현재 정책 𝜋 아래에서 모든 가능한 다음 상태들의 가치에 대한 평균을 의미합니다. 즉, 이 기대값은 현재 상태에서 취한 행동으로 인해 이동할 수 있는 모든 다음 상태들에 대한 가치의 가중 평균을 계산한 것입니다.

네 번째 단계로 넘어갈 때, 이 기대값을 계산하는 데 정책 𝜋를 직접 사용하는 대신, 환경의 전이 확률 𝑝을 사용하여 확률적인 특성을 더 명확하게 반영합니다. 그 결과, 방정식은 현재 상태와 행동, 그리고 다음 상태에 따른 환경의 동적인 특성을 기반으로 한 가치 함수의 기대값을 나타내게 됩니다.

결과적으로 Q 함수를 V 함수로 표현함으로써 A함수를 다음과 같이 표현할 수 있습니다.

A^\pi(s_t,a_t)=r(s_t,a_t)+V^\pi(s_{t+1})-V^\pi(s_t)

따라서 결국 알고리즘은 V함수에 대해서 fitting하면 됩니다.

Policy Evaluation

자, 그럼 정책을 어떻게 평가할 수 있을까? V함수는 상태 가치 함수로, 현재 주어진 상태에서 선택 가능한 모든 액션들을 선택할 때 예상되는 보상의 평균이다. 이를 표현하면 다음과 같다.

V^\pi(s_t) = \sum^T_{t'=t}\mathbb{E}_\pi[r(s_{t'},a_{t'})|s_t]

이를 이용해서 Estimator $J(\theta)$ 를 다르게 표현할 수 있다.

J(\theta)=\mathbb{E}_{s_1 \sim p(s_q)}[V^\pi(s_1)]

초기 상태의 분포(state distribution)에 대한 상태 가치 함수의 기댓값이다. 그러면 이제 상태 가치 함수에 대한 값을 알면 목적 함수를 구할 수 있다. 가장 대표적인 방법으로 Monte Carlo를 사용한 경험적 샘플(에피소드)에서 얻은 보상을 활용하는 것이다.

V^\pi(s_t) \approx \sum^T_{t'=t}r(s_{t'},a_{t'})

이제 이 답안지를 가지고 V함수를 approximation하면 더 나은 성능을 보일 수 있다. 즉, 이 경험적 샘플을 가지고 generate training data ${(s_t, \sum^T_{t'=t}r(s_{t'},a_{t'}))}$ , 이때 $\sum^T_{t'=t}r(s_{t'},a_{t'})$ 이 target value $y_i$ 이 된다.

L(\phi) = \frac{1}{2}\sum_i || \hat{V}^{\pi}_{\phi}(s_i)-y_i||^2

이때 target value $y_i$ 는 Monte Carlo estimation of the Q function이기도 하다.

Implementing Neural Network Baselines

\nabla_{\theta}J(\theta) \approx \frac{1}{N}\sum_{i=1}^{N}\sum_{t=1}^{T-1}\nabla_{\theta}log{\pi_\theta}(a_{i,t}|s_{i,t})((\sum_{t'=t}^{T-1}\gamma^{t'-t}r(s_{i,t'},a_{i,t'}))-V^{\pi}_{\phi}(s_{i,t})

Experiment 4 (HalfCheetah)

HalfCheetah-v2 벤치마크 환경에서 신경망을 이용한 Baseline을 적용했을 때 성능에 대해 확인해보았다.

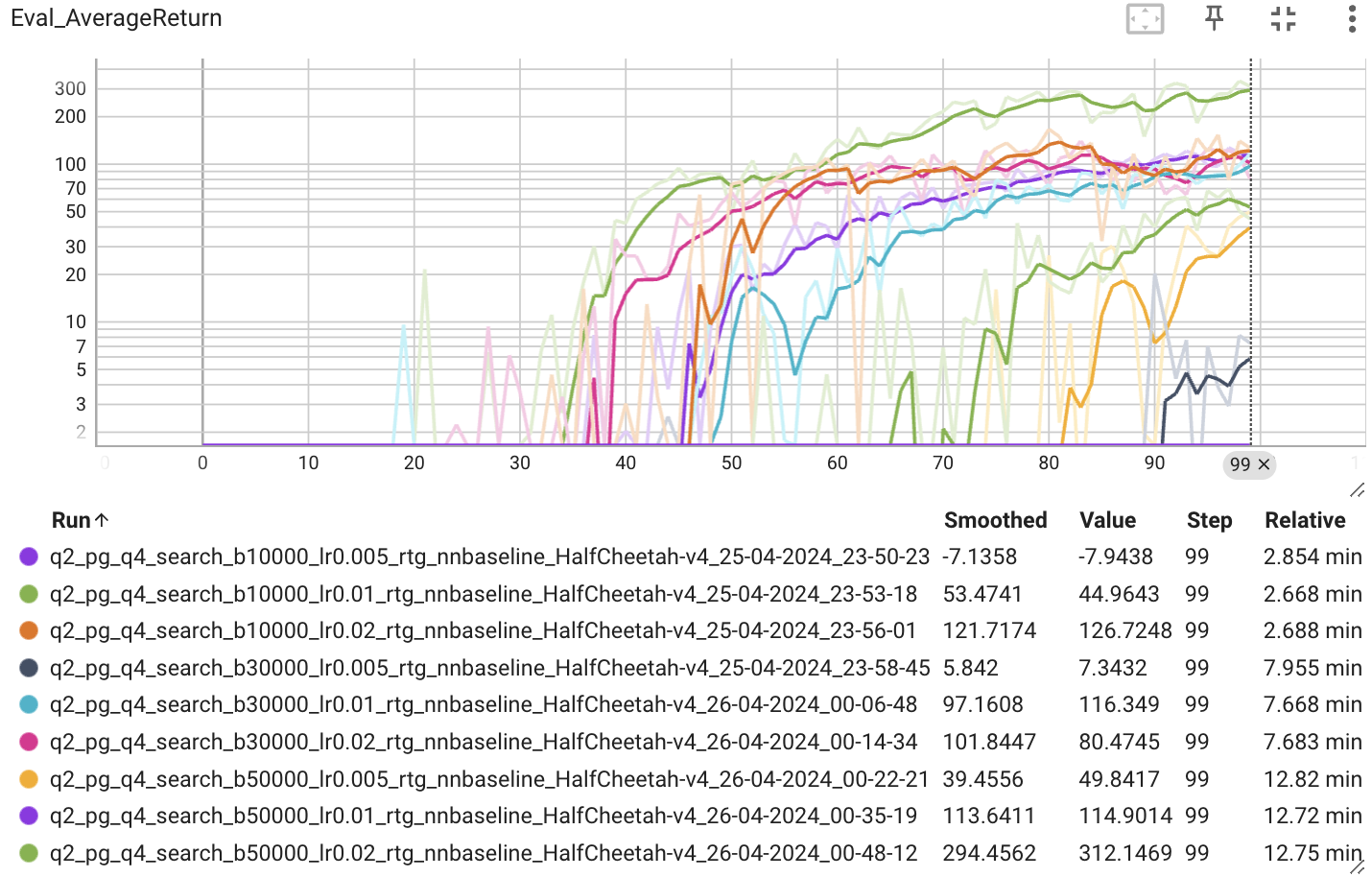
먼저 배치 사이즈 [10000, 30000, 50000], 학습률 [0.005, 0.01, 0.02]일 때 비교해보자.

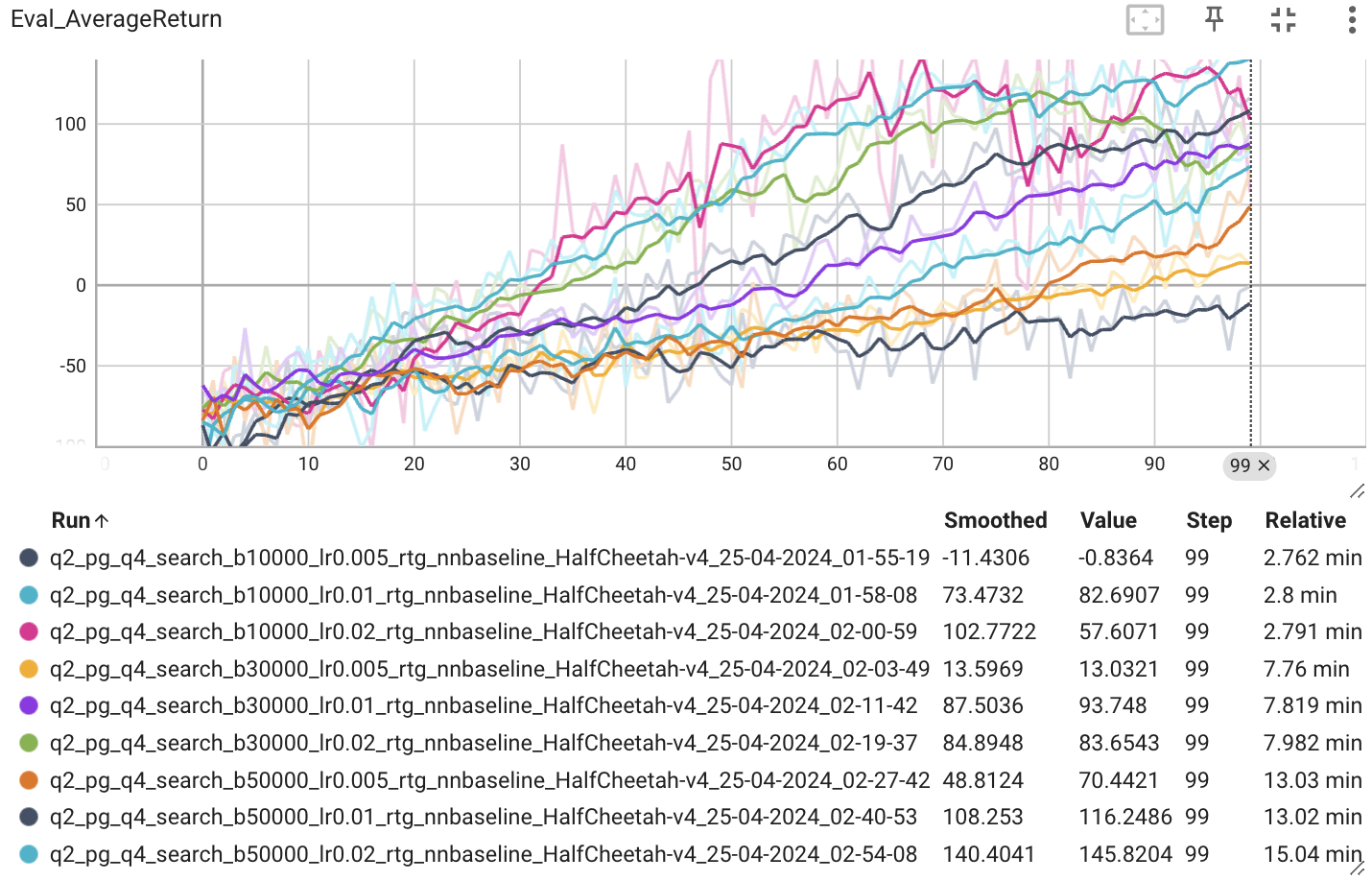
학습률은 0.02일 때가 평균 보상이 가장 높았고, 배치 사이즈는 클수록 높은 경향을 보였다. 배치 사이즈는 한번의 업데이트에 사용되는 샘플 수를 의미하는데, 그 샘플 수가 크면 다양한 상황에 대한 학습이 가능해 보다 일반화된 정책을 학습할 수 있을 것이다. 결국 Gradient의 Estimator 분산을 낮출 수 있다. 하지만 컴퓨팅 자원과 메모리 문제 등으로 인해 배치 사이즈를 무한정으로 키울 수는 없기에 이 같은 실험을 통해서 적절한 배치 사이즈를 찾는 것이 필요하다.

결과적으로 배치 사이즈 50000, 학습률 0.02일 때 최적의 결과가 나오는 걸 확인할 수 있다.

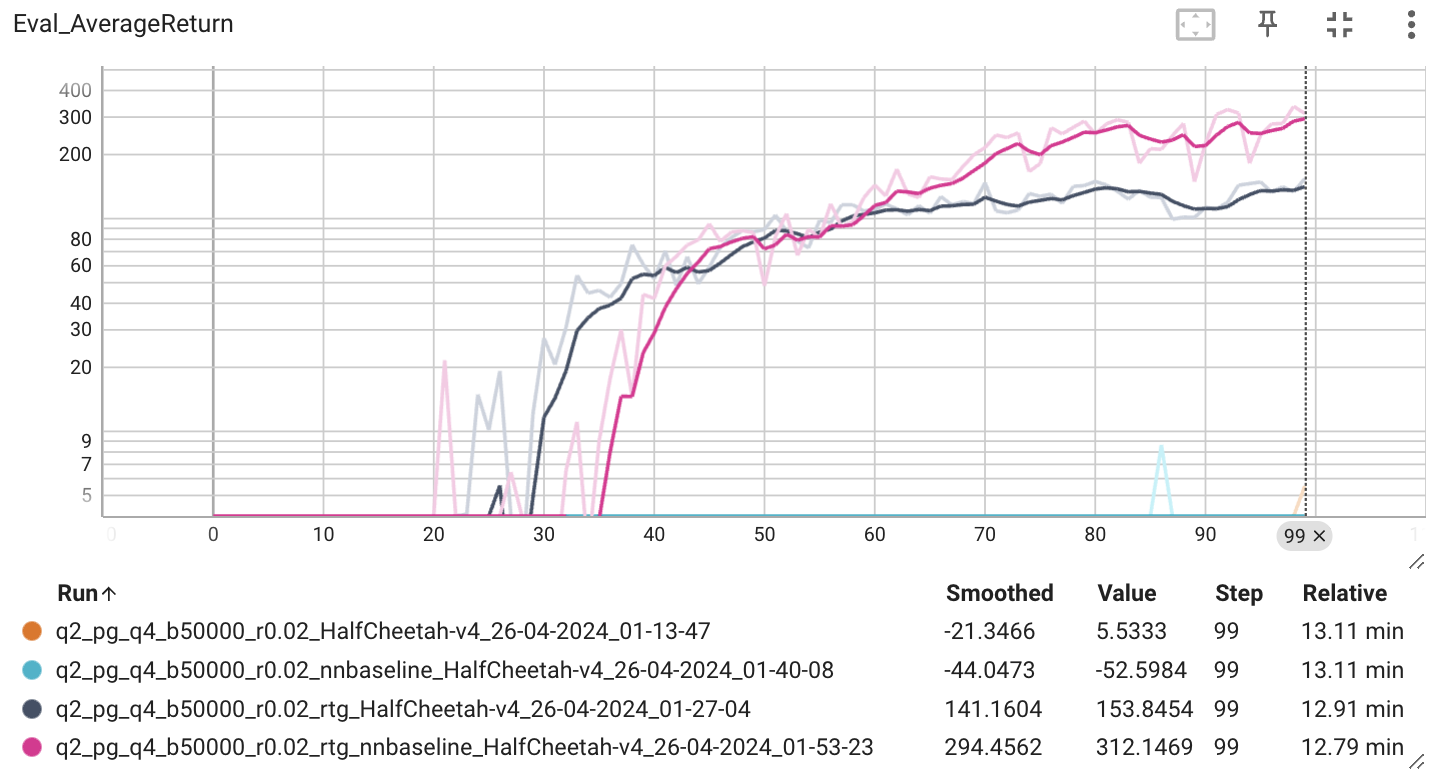
다음으로 찾은 최적의 배치 사이즈와 확습률을 이용해 r.t.g와 baseline이 모델의 성능에 미치는 영향에 대해서 확인해보았다.

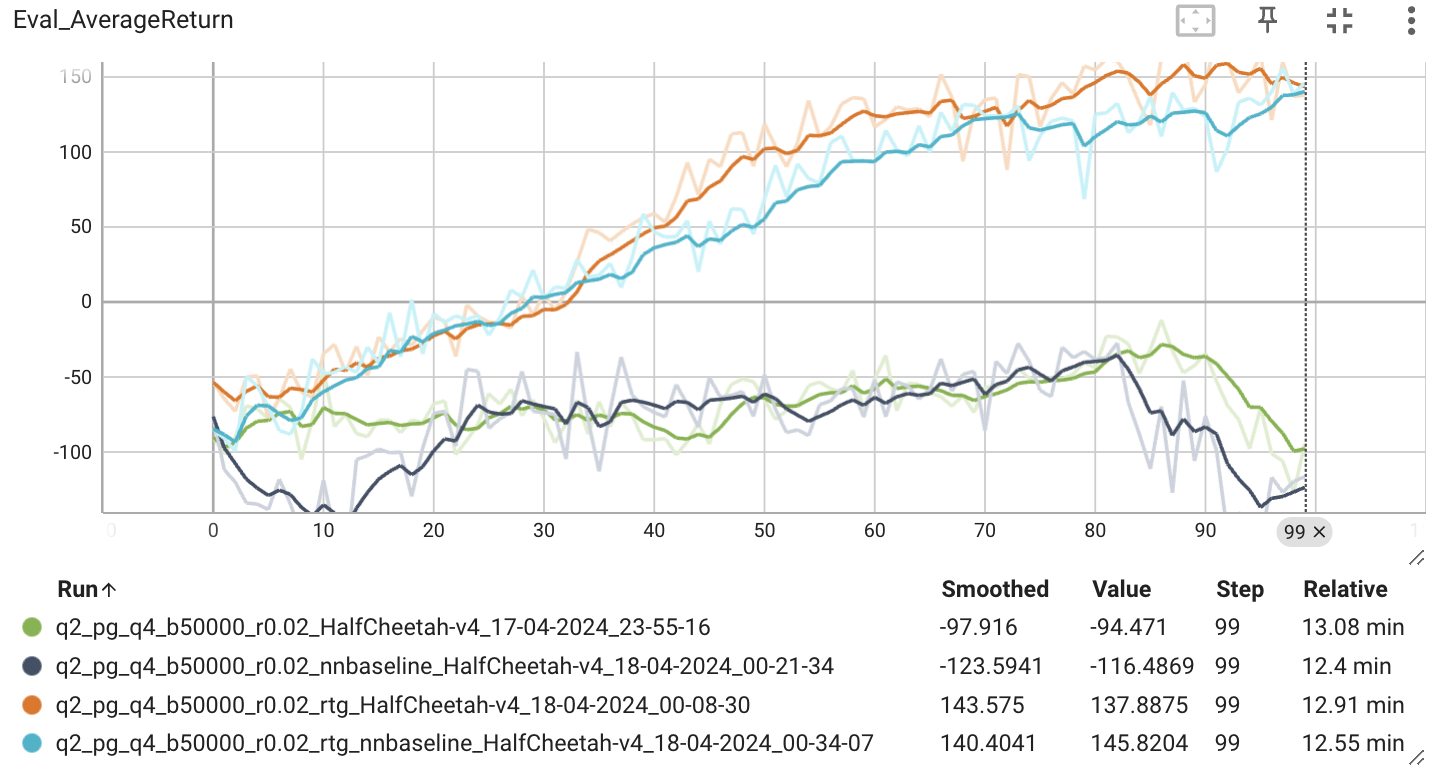
r.t.g와 baseline을 적용했을 때 가장 높은 성능을 보이는 것을 확인할 수 있다. 근데 과제에서는 200점에 가깝게 결과가 나와야 한다고 하는데 그렇지 못한 걸 볼 수 있다. 여러 시도 끝에 이 문제를 해결할 수 있었는데, 이에 대해서 생각해보자.

class MLPPolicyPG(MLPPolicy):
    def __init__(self, ac_dim, ob_dim, n_layers, size, **kwargs):

        super().__init__(ac_dim, ob_dim, n_layers, size, **kwargs)
        self.baseline_loss = nn.MSELoss()

    def update(self, observations, actions, advantages, q_values=None):
        observations = ptu.from_numpy(observations)
        actions = ptu.from_numpy(actions)
        advantages = ptu.from_numpy(advantages)

		# 현재 정책
        ac_dist = self.forward(observations)
        log_policy = ac_dist.log_prob(actions)

        # calculate loss
        loss = -(log_policy * advantages).mean()
        
        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

        if self.nn_baseline:            
            # Normalizing q_values (mean 0, std 1)
            qval_norm = (q_values - q_values.mean()) / (q_values.std() + 1e-8)
            # convert q_values into a tensor
            qval_tensor = ptu.from_numpy(qval_norm)

            # predict baseline using baseline_network
            baseline_pred = self.baseline(observations).squeeze()

            # Calculate Loss of baseline
            baseline_loss = self.baseline_loss(baseline_pred, qval_tensor)

            # Backprop baseline Loss
            self.baseline_optimizer.zero_grad()
            baseline_loss.backward()
            self.baseline_optimizer.step()

        train_log = {
            'Training Loss': ptu.to_numpy(loss),
        }
        if self.nn_baseline:
            train_log["Baseline Loss"] = baseline_loss
        return train_log

Policy Gradient를 계산해주는 클래스 MLPPolicyPG이다. 정책에 대한 Gradient를 계산할 때 Loss를 다음과 같이 정의했다.

loss = -(log_policy * advantages).mean()

근데 이걸 mean()이 아니라 sum()으로 바꿔주니까 결과가 좋아졌다.

Eony_Jahng

7층에 사는 동언이

이전 포스트

Policy Gradients_Reward-to-go [CS285_HW2]

다음 포스트