Backpropagation이 진짜로 하는 일? | Chapter 3, 딥러닝에 관하여 [3Blue1Brown]

각 오차는 오차함수가 각 가중치와 편차에 얼마나 민감한지를 나타내는 것이다.

Cost Function, 즉 Loss Function은 수만가지의 Train sample(input data)에 대한 오차를 평균화 한다.

위와 같이 단 하나의 이미지, 즉 단 한개의 image input (label=2)이 들어간다고 생각해보자
(784개의 input, 이는 1개의 image 28x28 pixel값) 그러면 맨 우측의 10개의 output units의 0.0~1.0까지의 숫자처럼 output이 나올 것 이다.

우리는 정답 2가 나오길 원하므로 2를 제외한 0~9까지의 output은 감소하고 2의 output은 증가하길 바란다.

그런데 증가와 감소의 정도 는 어느정도여야할까?
당연히 잘못나온 애들은 많이 조정되어야 하고, 적당히 잘나온 애들은 적게 조정되어도 될 것이다.

(위 그림에서 4번째, 7번째 output, 즉 Class 3,6의 output은 1.0이므로 0이 되게끔 많이 감소가 되어야 할 것이다. / 이에 반해 Class 9의 output은 0.1이므로 0이 되게끔 적게 감소시키면 될 것이다.)

조정해야되는 '정도' 는 '오차' 와 관련되어있다

---

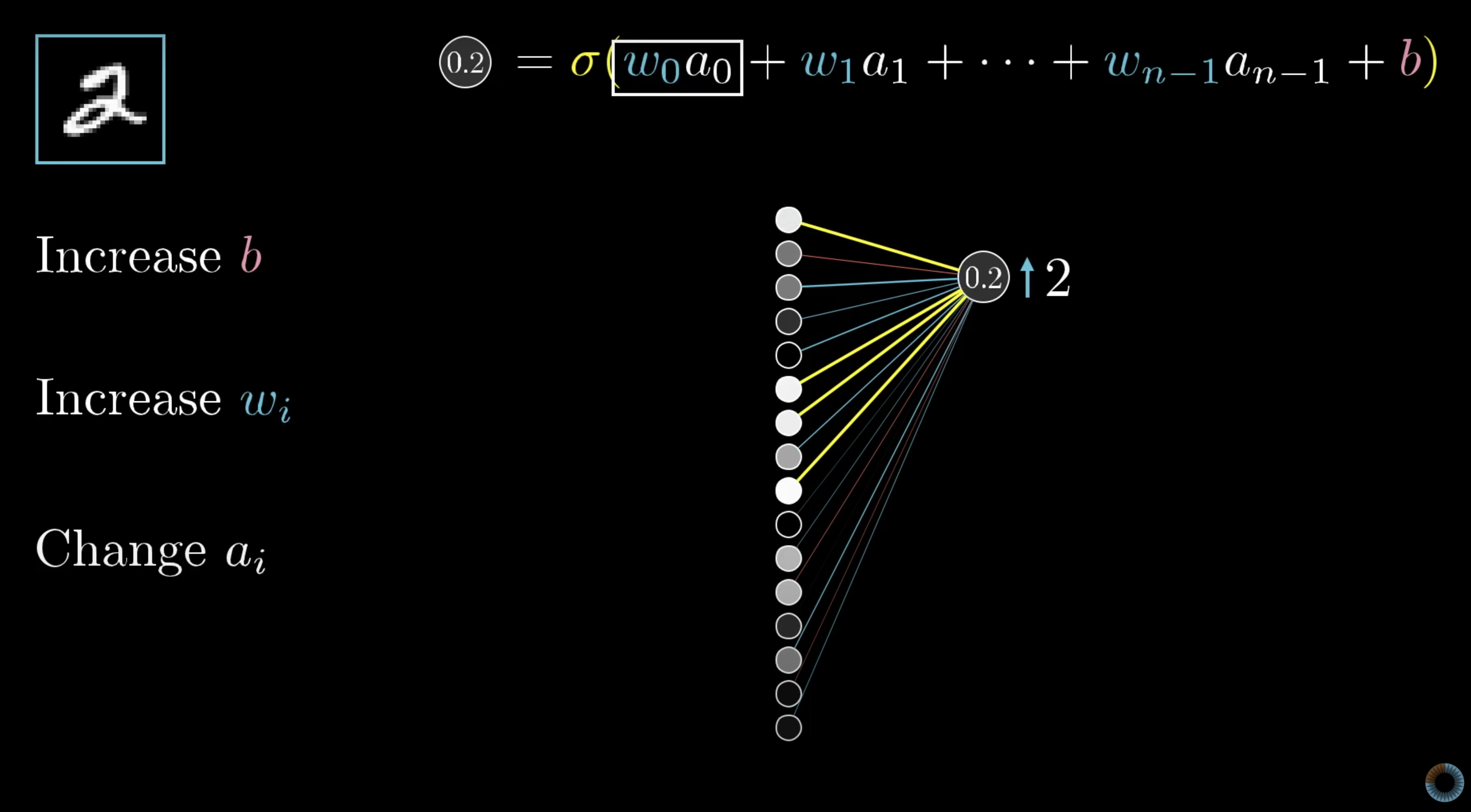
자 이번에는 우리가 변화시키려는 Class 2의 output node만 콕 찝어서 봐보자.
0.2가 나온 세번째 output node (Class 2)는 위의 그림과 같이 이루어져있다.

수많은 input들 $a_n$들과 $w_n$들의 곱의 합과 bias, 그리고 Activation function을 통해서 0.2라는 값이 나온 것 이다. 즉 우리가 0.2를 1로 만들기 위해 조절할 수 있는 변수가 3개인 것!

${\color{green}w_i},\;a_i,\;bias$

우리는 $w_i$에 집중해보자.

---

한가지 예시를 들어보자. 아래의 수식에서 $a_0$이 매우 큰 반면, $a_1$이 매우 작다면?
이 경우에 $w_0$과 $w_1$ 둘 중 어느것을 조절하는 것이 output값, 즉 0.2에 큰 변화를 줄까?

당연히 $a_0$에 붙어있는 $w_0$은 조금만 변화해도 매우 크게 영향을 줄 것 이다. $=$ "강하게 연결되어 있다"

단순하게 이야기하면 2 image를 봤을 때 켜지는 뉴런들은 2에 대해서 생각할 때 더 강하게 켜진다.

---

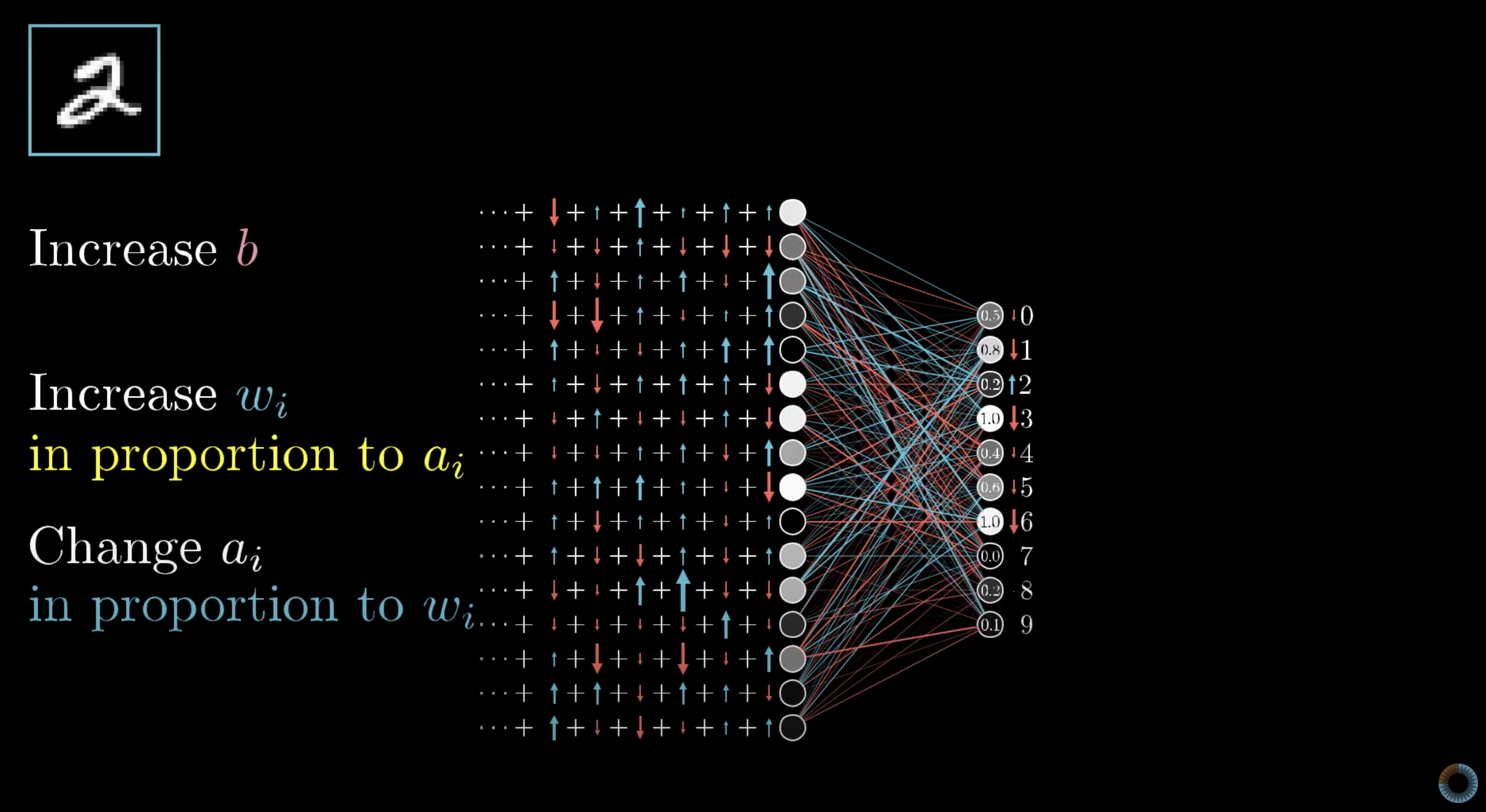
바로 위에서는 Class 2의 output node만 콕 찝어서 봤었고 이번에는 0~9까지의 output node들에 대해서 생각하면 위 그림과 같다.
위 그림에서 변경해야될 정도들, 즉 빨간색 파란색 화살표들을 모두 더하면 해당 층에서 변경되어야할 정도를 알 수 있다.
음... $w$와 $a$

---

Batch와 Stochastic Gradient descent

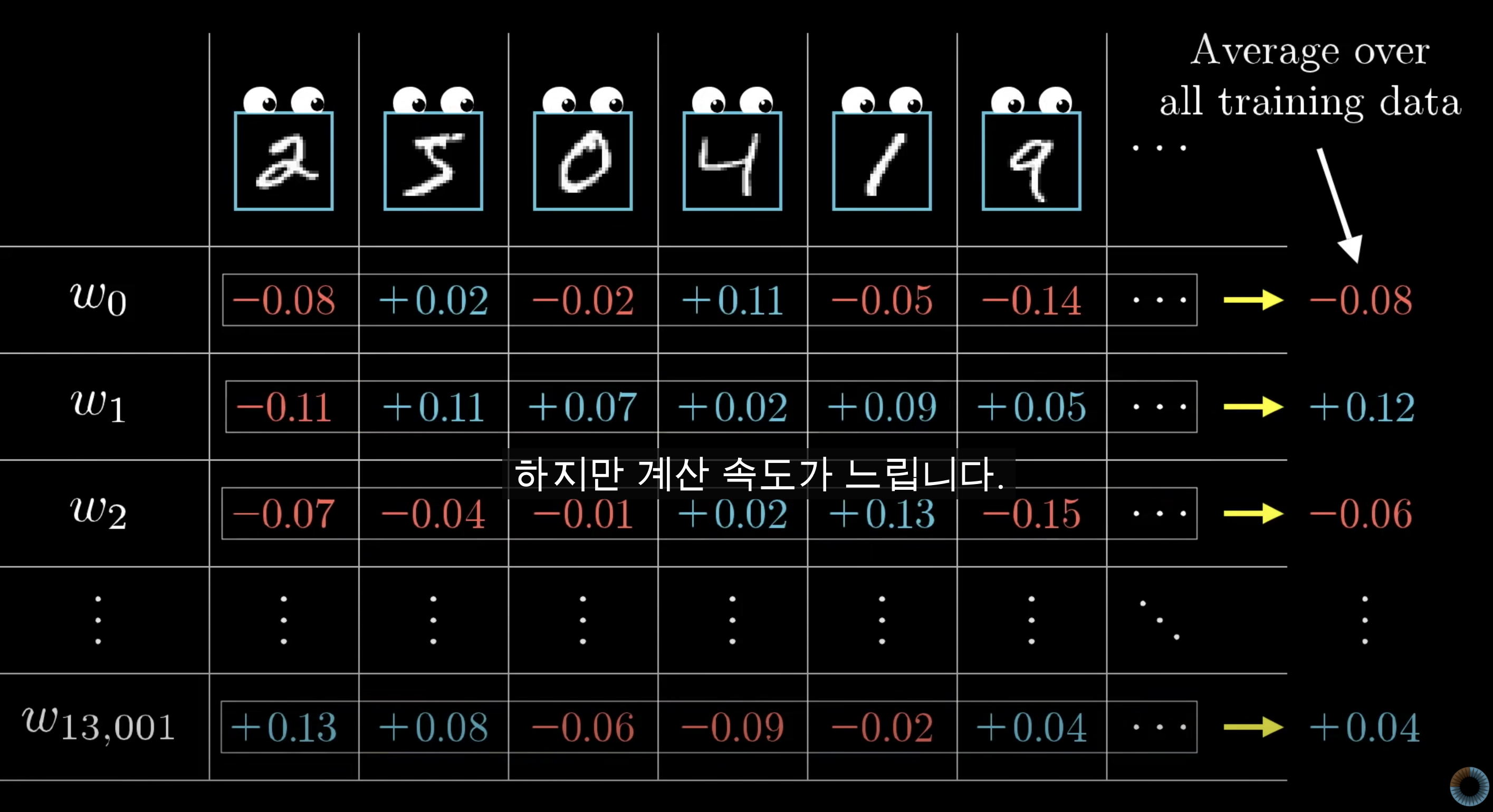
자 원래 우리는 우리가 가진 데이터 한바퀴당, 즉 1번의 epoch당 1번의 Step을 밟음.

각각의 데이터가 뱉는 output의 Cost(Loss) 구하는 것을
우리가 가진 데이터의 수만큼 반복해서 모~두 종합하여 최적의 Gradient Descent Step을 밟음. (위 그림처럼!)

그런데 데이터가 수억, 수만개 있으면 언제 그걸 다 돌려서 Gradient descent step 한번 밟고 앉아있냐!?

$\therefore$ 데이터를 나누자! $\rightarrow$ Batch

그러면 하나의 Batch dataset에 대한 Gradient가 구해지면 바로 Gradient descent step을 밟을 수 있음

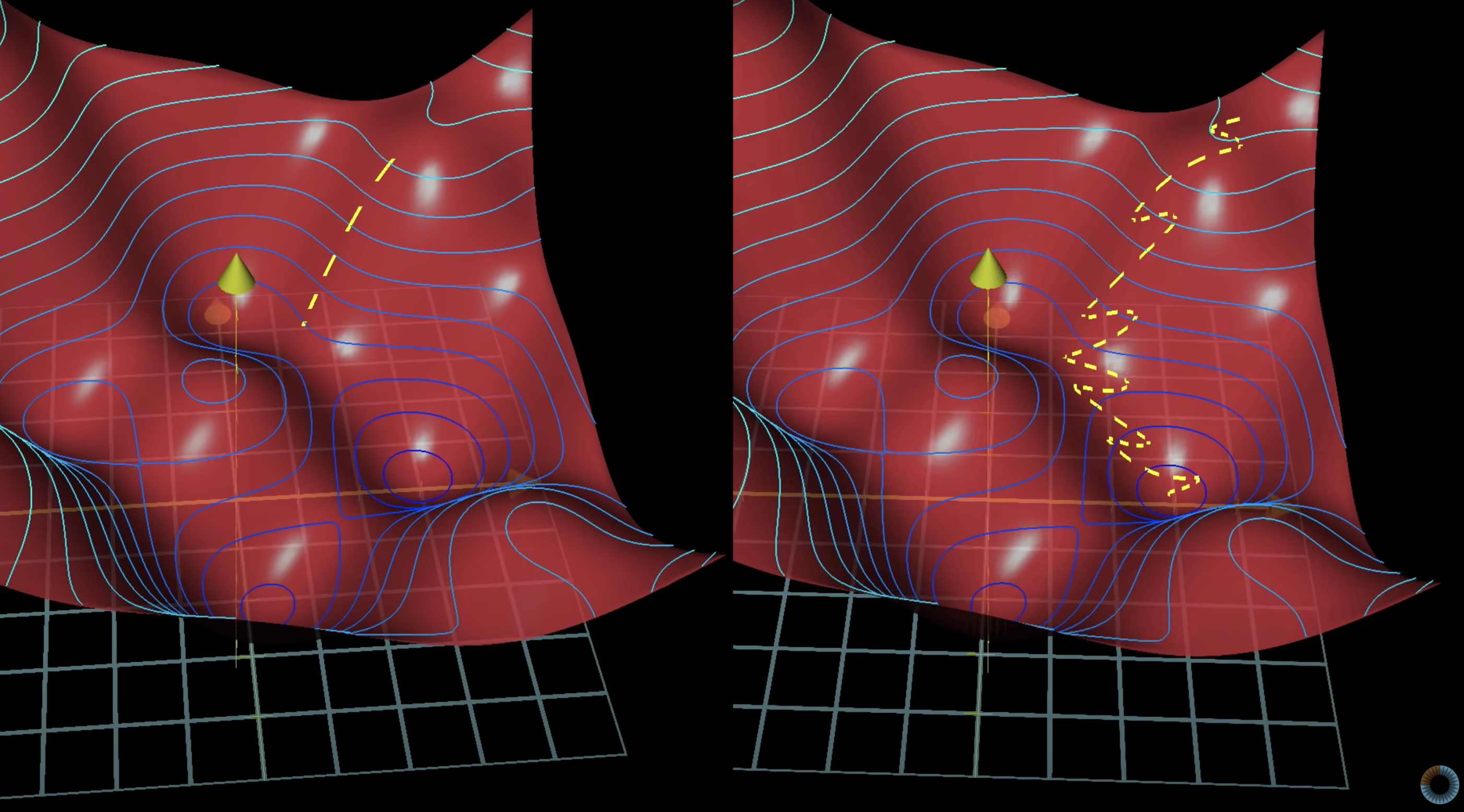
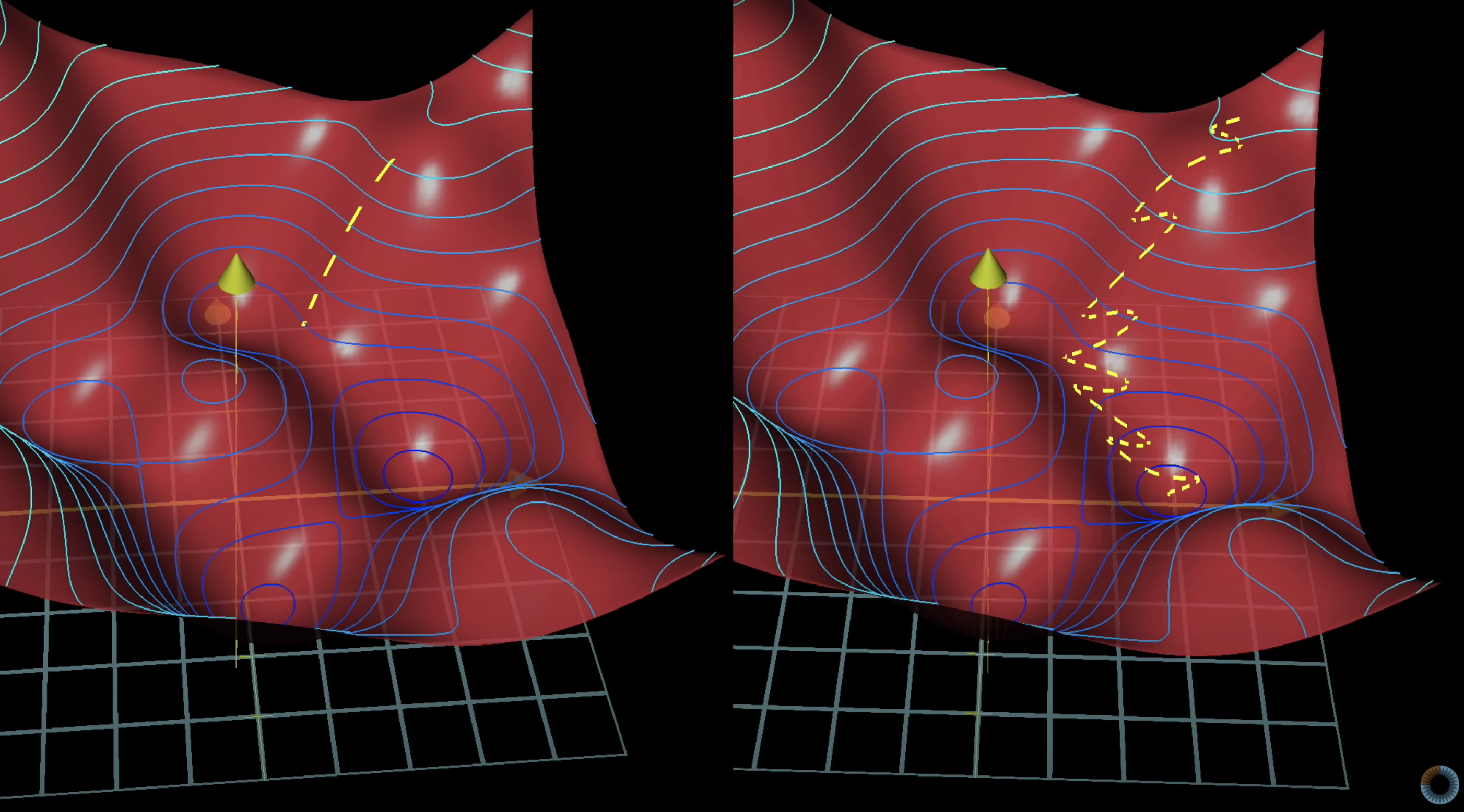
Batch의 효율성을 잘 나타낸 그림이다.

• 왼쪽은 아주 정확하게 저점을 향해 똑바로 내려가고 있다. 근데 매우 신중하게 방향을 선택해서 좀 답답함.
• 오른쪽은 다소 술취한 사람처럼 왔다갔다하지만 어찌되었든 저점을 향해 가고 있다. 시원시원하게 방향을 선택해서 꽤나 걸음걸이가 빠름

데이터의 분포는 확률분포를 따를 것이다. 따라서 부분부분의 데이터셋, 즉 Batch Dataset을 통해서 Gradient Descent를 진행하여도 확률적으로 잘 descent 될것이다
$\rightarrow$ Stochastic Gradient Descent [?]