Filter 그리고 Sobel Kernel

olxtar·2022년 4월 13일

[영상처리강좌] 소벨 검출이란? 소벨 엣지 검출기 알아보기(sobel edge detection)

0. Sobel operator

The Sobel operator, somtimes called the Sobel filter( $\simeq$ Sobel Kernel), is used in image processing and computer vision, particularly within edge detection algorithms where it creates an image emphasising edges.
...
Technically, it is a discrete differentiation operator, computing an approximation of the gradient of the image intensity function. At each point in the image, the result of the Sobel-Feldman operator is either the corresponding gradient vector or the norm of this vector.
discrete differentiation : 불연속 미분?
이미지의 각 포인트에서의 Sobel operator의 결과물은 gradient vector or norm of this vector이다.

Formulation

The operator uses two 3x3 kernels which are convolved with the original image to calculate approximations of the derivatives one for horizontal changes, and one for verticla.

If we define $A$ as the source image, and $G_x$ and $G_y$ are two images which at each point contain the horizontal and vertical derivative approximations respectively, the computations are as follows:

G_x = \begin{bmatrix}+1 & 0 & -1 \\ +2 & 0 & -2 \\ +1 & 0 & -1\end{bmatrix}*A

G_y = \begin{bmatrix}+1 & +2 & +1 \\ 0 & 0 & 0 \\ -1 & -2 & -1\end{bmatrix}*A

G = \sqrt{G_x^2+G_y^2}

$A:$ source image, 즉 input
$*$ : convolution operator, 즉 Matrix 각 위치의 요소끼리 곱해줌
$G_{x,y}$ : 각 포인트마다 x축(horizontal), y축(vertical) derivative approximation이 있는 output image
$G$ : 두 Gradient ( $G_{x,y}$ )에 대한 Magnitude [?]

Sobel Filter에 대해 더 자세히 배우기 전에 일단 Filter에 대한 기본 개념부터 학습해보자!

1. Filter?

00. 기초 개념

Edge란?

이미지,영상에서의 Edge는 픽셀값이 한쪽으로 급격히 변하는 부분을 가리킵니다.
어둡다가 밝아지거나 밝다가 어두워지는 부분으로, 일반적으로 사물과 사물, 사물과 배경의 경계에서 Edge가 발생하므로, 이를 추출해내는 것은 매우 중요함.

기본적으로 Edge를 찾아내기 위해선 픽셀값의 변화율을 측정합니다. 이 변화율이 큰 픽셀이 바로 Edge! 변화율? 미분(derivative)이잖아?

f'(x)=\frac{d}{dx}f(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}

그런데 이미지, 영상의 경우 함수 즉, $f(x)$ 로 이루어지지 않으므로...

2차원 평면에서 정의된 함수 f(x,y)
정수 단위 좌표에 픽셀값이 나열되어 있는 이산(discrete) 함수 픽셀의 위치는 좌표평면에서 1,2,3...으로 나타내잖아! 연속이 아니지!

2차원 평면에서 정의된 함수 $\rightarrow$ x, y에 대해서 각각 Partial Derivative(편미분)
정수 단위 좌표에 픽셀값이 나열되어 있는 이산(discrete) 함수 $\rightarrow$ 이산함수의 미분, 즉 Discrete Differenation(차분)

뭐 편미분에 대한 개념은 대충 알고있으니 차분에 대해서 알아보자

이산함수의 미분
= discrete differenation, Derivative approximation(미분근사화)

[!] $f(x)$ 는 이산함수, 즉 $x=1,2,3...n$

Forward difference approximation (전진차분근사)

\frac{f(x+h)-f(x)}{h}

Backward difference approximation (후진차분근사)

\frac{f(x)-f(x-h)}{h}

Centered difference approximation (중앙차분근사)

\frac{f(x+h)-f(x-h)}{2h}

ex)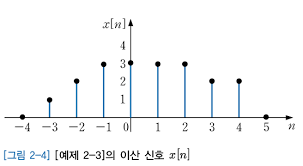

위 그래프에서의 x[n] = f(x)라고 생각하고 중앙차분근사를 해보자(x=4일때)

$\frac{f(x+h)-f(x-h)}{2h}$

$x=4, {\color{orange}h=1}$ 일때

$\frac{f(4+{\color{orange}1})-f(4-{\color{orange}1})}{2\cdot{\color{orange}1}}=\frac{f(5)-f(3)}{2}=\frac{0-2}{2}=-1$

흠...x축으로 두칸 이동시 y값이 두칸하락함... 따라서 기울기가 -1
이게 x=4인 지점에서의 기울기느낌(?)

미분 마스크

[?] 마스크? kernel같은건가?

중앙차분을 위한 마스크는...

x축 방향의 미분으로는

\begin{pmatrix} -1 & 0 & +1\end{pmatrix}

y축 방향의 미분으로는

\begin{pmatrix} -1 \\ 0 \\ +1 \end{pmatrix}

위의 마스크로 마스크 연산을 수행하고 2로 나눠주면 매우 쉽게 '0'에 위치하는 타겟 픽셀의 대한 미분값을 알아낼 수 있다. 음 그냥 Convolution 연산인가? 합성곱!?

ex1)
자 위의 중앙차분 예시를 다시 가져와보자

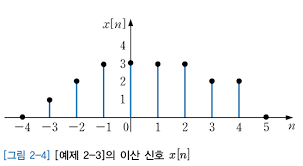
우리에게 주어진 source image의 pixel값을 $f(x)$ , 좌표값을 $x$ 라고 해보자. ~~(이미지가 x축으로 한줄만 있다 생각하셈, 그리고 위 그래프 값에 기반한다면...)~~

input = \begin{pmatrix} 2 & 2 & 0 \end{pmatrix}

mask = \begin{pmatrix} -1 & 0 & 1 \end{pmatrix}

input * mask = \begin{pmatrix} 2 & 2 & 0 \end{pmatrix}*\begin{pmatrix} -1 & 0 & 1 \end{pmatrix}=-2+0+0=-2

이걸 2로 나눠주면?
$-1$ (중앙차분 연산 결과와 같음)

그래디언트

다차원 인자 ex) x,y에 대하여 편미분을 하면 미분값도 다차원이 되며, 이것을 그래프로 나타낼 시 마치 다차원적 경사처럼 표현됩니다.

x,y에 대한 편미분값을 하나로 묶어 벡터화 한 것을 gradient라고 합니다.

Gradient Magnitude
$\sqrt{\frac{\partial f}{\partial x}^2+\frac{\partial f}{\partial y}^2}=\sqrt{\frac{\partial}{\partial x}f(x,y)^2 + \frac{\partial}{\partial y}f(x,y)^2}$
Gradient direction
$\theta=\tan^{-1}(\frac{\frac{\partial f}{\partial y}}{\frac{\partial f}{\partial x}})$

위와 같은 식으로 타겟 픽셀과 주변 픽셀간의 차이와 방향, 즉 Edge을 알아낼 수 있습니다.
다만 이것이 Edge이다, Edge가 아니다를 분류하기 위해서는 기준치가 필요합니다.
예를 들어서 주변 픽셀과의 차이가 고작 1인데 이걸 Edge로 인정해야하나?

이러한 기준이 되는 값을 임계값(threshold)이라고 합니다.
임계값이 높으면 밝기차이가 급격한 Edge만 검출,
임계값이 낮으면 밝기차이가 낮은 Edge를 검출하게됨.

01. 기본 용어

Filtering

필터링이란? 어려울것없다. 그냥 알고있는 무엇을 걸러내는 필터링 이라고 생각하면된다.
~~그런데~~ '무엇'에 따라 뭔가 필터링 같지 않을 수 있다. 무슨 말이냐면

이미지에서 노이즈를 걸러내는 필터~~(이건 굉장히 일반적인 느낌의 필터링!)~~
이미지에서 부드러운 느낌의 부분들을 걸러내면 이미지가 날카로워(?)진다.
이미지에서 급격하지 않게 변화하는 부분들을 걸러내면 이미지의 Frequency가 높은 부분만 살아남을 것이다. ~~(High-pass filter, Edge Detection)~~

즉 어찌보면 무언가를 걸러냄으로써 어떤 부분을 더 돋보이게 할 수 있다 이 말임...

Filter

= Filter, mask, kernel, window

Convolution

\begin{bmatrix} v_{-1,-1} & v_{0,-1} & v_{+1,-1} \\ v_{-1,0} & {\color{orange}v_{0,0}} & v_{+1,0} \\ v_{-1,+1} & v_{0,+1} & v_{+1,+1} \end{bmatrix}*\begin{bmatrix} k_a & k_b & k_c \\ k_d & k_e & k_f \\ k_g & k_h & k_i \end{bmatrix}

좌측의 matrix를 $v$ $\simeq$ (input image의 pixel value)
우측의 matrix를 $k$ (kernel, filter, mask, window) 라고 하면...
$\times$ : element-wise 곱 연산, 즉 각 행렬의 같은 위치의 요소끼리의 곱

=sum[v \times k]

이것이 바로 컨볼루션(= Convolution, 합성곱, Filter operation, Correlation)이라고 한다.

[!] $sum[v\times k]$ 는 1x1 사이즈인 scalar값 아니냐!?
[+] 이와 같은 Convolution operation(=컨볼루션 연산, 필터링 연산...등)을 하면 input matrix에 비해 output matrix는 크기가 줄어들 수 밖에 없다. 아래처럼 말이지...

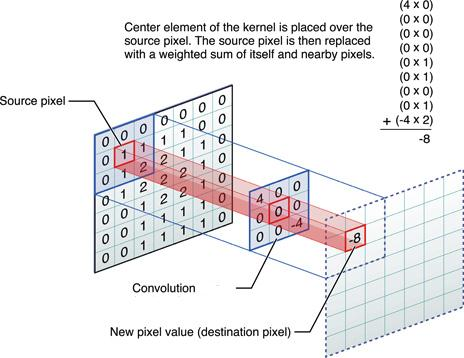
Striding

매우 큰 input matrix에 비해 kernel matrix는 보통 3x3이므로 kernel matrix가 옮겨가면서 컨볼루션 연산을 함. 이 옮겨가는 칸(matrix 요소)의 수가 바로 Striding임.

Padding

위에서 언급한거처럼, Convolution operation 이후에는 input matrix, 즉 원본 이미지 크기가 줄어들 수 밖에 없는데 이를 원래와 같이 유지하고자 하는 방법이 바로 Padding입니다. 다양한 값이 될 수 있지만 패딩은 그냥 원본이미지의 동서남북으로 Pixel을 추가한다라고 생각하면 됨.

Output matrix 크기에 대한 공식

Output Height = (Height + 2Padding - Filter Height) / Striding) + 1
Output Width = (Width + 2Padding - Filter Width) / Striding) + 1
Output matrix size = (Size + 2Padding - Filter Size) / Striding) + 1 (input, filter size가 정방형 일때)

ex)
Input image size : 4x4
Padding : 1
Filter size : 3x3
Striding : 1
Output matrix size : ?

단순하게 생각하셈 4x4사이즈 이미지에다가 패딩 1씩 붙이면? 6x6
그 안에서 3x3 필터가 한칸씩 움직이면 몇 사이즈의 아웃풋이 나올까? -> 4x4
[!] Padding이 1이라는 것은 동서남북으로 1줄씩 붙여주는것이므로 1의 2배가 사이즈에 +된다. 즉 4x4사이즈 + 패딩 1 = 6x6 사이즈

Output matrix size = ((4 + 2*1 - 3) / 1 ) + 1 = 4

2. 다시 Sobel Filter

... 중앙차분을 위한 마스크는...

x축 방향의 미분으로는 $\begin{pmatrix} -1 & 0 & +1\end{pmatrix}$

y축 방향의 미분으로는

$\begin{pmatrix} -1 \\ 0 \\ +1 \end{pmatrix}$ ...

프로그램적으로 2차원 영상 또는 이미지 데이터를 분석할때, 마스크 연산(Filtering, Kernel Operation)을 주로 사용합니다. 앞서 배웠던 중앙차분 마스크 ${\color{orange}(\uparrow)}$ 처럼 Edge를 검출할 수 있는 편미분 계산을 함.
잠깐 생각해보면 좋은게 1024x1024 pixel의 이미지에서 위와 같은 3x1, 1x3 사이즈의 커널로 필터링을 하면 Edge를 검출하기 힘들지 않을까? 고양이와 배경의 경계 즉, Edge가 1 pixel 단위로 나타날까? 이런말임
또한 노이즈와 같은 패턴이 이미지 데이터 안에 있을 수 도 있고...

따라서 이러한 문제점(?)에 대항하는 조금 더 범위가 큰 여러 미분 마스크가 개발됨.
그 중 유명한 것이 바로 Sobel Kernel.

S_x= \begin{bmatrix} -1 & 0 & +1 \\ -2 & 0 & +2 \\ -1 & 0 & +1 \end{bmatrix}

S_y= \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ +1 & +2 & +1 \end{bmatrix}

S_x^T=S_y

현재 행 or 열에 대한 중앙차분 연산을 2회 수행하고
이전 행 or 열, 이후 행 or 열에 대한 중앙차분 연산을 각각 1회씩 수행

$\therefore$ 3x1, 1x3 미분 마스크와 같이 타겟 픽셀이 포함된 행 또는 열에 대한 변화율만 고려하는 것이 아닌 타겟 픽셀의 인근 픽셀( $S_x$ : 상,하 / $S_y$ : 좌,우)까지 고려하여 사용함.

3. cv2.Sobel

OpenCV에서는 sobel 마스크를 이용하여 필터링을 적용해주는 cv2.Sobel. 함수를 제공.

cv2.Sobel(src, ddepth, dx, dy, 
		  dst=None, 
          ksize=None, 
          scale=None, 
          delta=None, 
          borderType=None)

src : soruce 즉, 입력 데이터(이미지 or 영상)
ddepth : 출력 데이터 타입, -1 이면 입력 데이터와 같은 데이터 타입 사용
dx : x 방향 미분 차수, 1차미분할지 2차미분할지...
dy : y 방향 미분 차수, 1차미분할지 2차미분할지...
dst : 출력 데이터(행렬) [?]
ksize : 커널의 크기. 기본값은 3
scale : 연산 결과에 추가적으로 곱할 값. 기본값은 1
delta : 연산 결과에 추가적으로 더할 값. 기본값은 0
borderType : 가장자리 픽셀 확장 방식. 기본값은 cv2.BORDER_DEFAULT

00. Practice

아래와 같은 경로에 다운받아놓은 춘식이 사진(springmeal.jpg)으로 OpenCV Sobel 필터 연습을 해보자

# 기본 세팅
import matplotlib.pyplot as plt
import matplotlib.image as mpimg

import cv2
import numpy as np

%matplotlib inline

# Read in the image
image = mpimg.imread('images/springmeal.jpg')

# Show image
plt.imshow(image)

# image color to gray
gray = cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)

plt.imshow(gray, cmap='gray')

Case 1 : default

Sobel_ = cv2.Sobel(src = gray,
          ddepth = -1,
          dx = 1,
          dy = 1,
          ksize = 3,               
          scale = 1,
          delta = 0
          )                      # 모든 argument들? parameter들을 디폴트값으로 함

plt.imshow(Sobel_, cmap='gray')

춘식이 어디갔노

Case 2 : kernel size 3 -> 5

Sobel_ = cv2.Sobel(src = gray,
          ddepth = -1,
          dx = 1,
          dy = 1,
          ksize = 5,
          scale = 1,
          delta = 0
          )                      # kernel size를 5로 늘려봄

plt.imshow(Sobel_, cmap='gray')

경계(?)가 더 잘나오긴 한다...

Case 3 : scale 1 -> 10

Sobel_ = cv2.Sobel(src = gray,
          ddepth = -1,
          dx = 1,
          dy = 1,
          ksize = 3,
          scale = 10,
          delta = 0
          )                      # scale을 10으로 늘려봄

plt.imshow(Sobel_, cmap='gray')

Default값에서 scale 즉, 연산결과에 곱해줄값을 1->10으로 하니 경계가 더 찐해졌다.
이게 뭔가 Threshold를 낮춘...? 즉 연산결과값에 10을 곱해줘버려서 약간의 값이라도 있는 pixel(밝기가 조금이라도 있는)을 강화시켜줌

Case 4 : kernel size + scale

Sobel_ = cv2.Sobel(src = gray,
          ddepth = -1,
          dx = 1,
          dy = 1,
          ksize = 5,
          scale = 3,
          delta = 0
          )                      # kernel size : 5, scale : 3

plt.imshow(Sobel_, cmap='gray')