
🟪 선택 정렬
- 선택 정렬 =
selection sort
🔶 방법
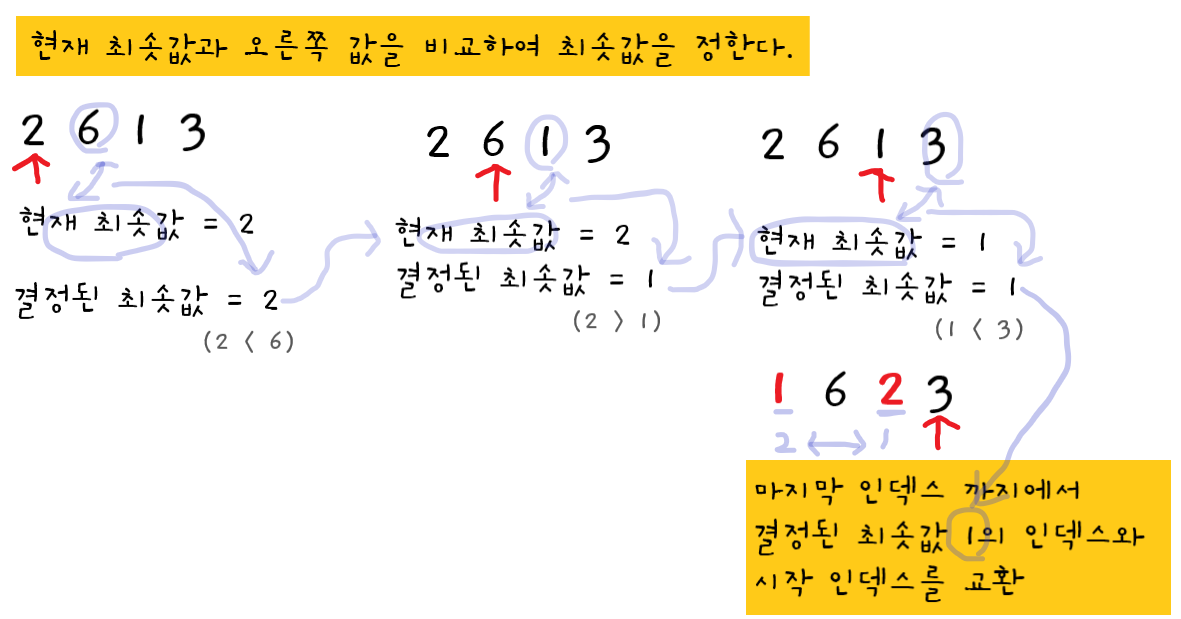
인덱스0까지에서 정해진 최솟값 = 2 (유일한 값이므로)
- ↳
인덱스0까지에서 정해진 최솟값2는인덱스1의 값6보다 작으므로 최솟값이2로 결정됐다.
인덱스1까지에서 정해진 최솟값 = 2
- ↳
인덱스2의 값1이인덱스1까지에서 정해진 최솟값2보다 작으므로 최솟값이1로 결정됐다.
인덱스2까지에서 정해진 최솟값 = 1
- ↳
인덱스2까지에서 정해진 최솟값1이인덱스3의 값3보다 작으므로 최솟값이1로 결정됐다.
- ↳ 이번 패스스루에서 정해진 최솟값
1의 인덱스인인덱스2와 이번 패스스루의 시작 인덱스인인덱스0을 교환한다.
(마지막 인덱스까지에서 정해진 최솟값은1이고 비교할 오른쪽 셀이 없으므로 이 최솟값이 이번 패스스루의 최솟값이 된다. )
1단계 : 현재 최솟값과 오른쪽 셀의 값을 비교하여 최솟값을 정한다.
현재 최솟값 : 지금 가리키고 있는 인덱스 까지 에서 정해진 최솟값
첫번째 패스스루의 첫 단계에서는 인덱스0과 인덱스1을 비교하여 최솟값을 정한다.
정해진 최솟값의 인덱스를 변수에 저장한다.
변수에 들어 있는 값보다 작은 값이 들어 있는 셀을 만나면 변수가 새 인덱스를 가리키도록 값을 대체한다.
2단계 : 배열의 끝에 도달하면 최솟값의 인덱스와 패스스루의 시작인덱스를 교환한다. 최솟값의 인덱스와 시작인덱스가 같은 위치면 교환이 일어나지 않으므로 이 단계 또한 일어나지 않는다.
패스스루를 시작했을 때 인덱스는 첫 패스스루에서는 인덱스 0이고, 두 번째 패스스루에서는 인덱스 1이다.
3단계 : 매 패스스루는 1, 2 단계로 이뤄진다. 패스스루의 시작인덱스가 배열의 마지막인덱스가 되기 전 까지 패스스루(1~2단계)를 반복한다. 즉 패스스루의 시작인덱스가 배열의 마지막인덱스 바로 전의 인덱스가 되면 마지막 패스스루가 된다는 뜻이다. 왜냐하면 패스스루가 끝나면 패스스루의 시작인덱스까지 올바르게 정렬된다. 그러므로 마지막 패스스루에서는 마지막 셀을 제외한 모든 셀이 올바르게 정렬이 되므로 이는 곧 전체 배열이 올바르게 정렬되는 것이기 때문이다.
🔶 {4, 2, 7, 1, 3} 정렬 해보기
🔵 첫 번째 패스스루

1단계 : 인덱스0에 들어 있는 값 4가 현재 최솟값이므로 이 인덱스를 변수에 저장한다. 그리고 현재 최솟값과 오른쪽 값 2를 비교하여 최솟값을 정한다. 오른쪽 값이 더 작으므로 결정된 최솟값은 2가 된다.
2단계 : 여기까지 정해진 현재 최솟값은 2이다. 다음 값인 7이 더 크므로 2가 최솟값으로 유지된다.
3단계 : 현재 최솟값 2와 다음 값 1을 비교한다. 오른쪽 값이 더 크므로 최솟값은 1로 새롭게 결정된다.
4단계 : 인덱스 3을 가리키고 있을 때 현재 최솟값은 1이다. 다음 값 3과 비교했을 때 여전히 최솟값이다. 배열의 끝 값과 비교했을 때 제일 작은 수를 알아냈으므로 전체 배열의 최솟값은 1로 결정됐다.
5단계 : 이번 패스스루에서 결정된 최솟값 1의 안덱스3과 이번 패스스루의 시작 인덱스인 인덱스0을 교환한다.
🔵 두 번째 패스스루

6단계 : 인덱스0은 첫 번째 패스스루에서 이미 정렬된 값이므로 두 번째 패스스루는 다음 인덱스인 인덱스1부터 시작한다. 인덱스1의 값 2가 현재 최소값이므로 이 인덱스를 변수에 저장한다. 현재 최솟값과 오른쪽 값 7을 비교하여 결정된 최솟값은 2이므로 변수는 그대로 유지된다.
7단계 : 현재 최솟값 2와 오른쪽 값 4를 비교하여 결정된 최솟값은 2이므로 변수는 그대로 유지된다.
8단계 : 현재 최솟값 2와 오른쪽 값 3을 비교하여 결정된 최솟값은 2이므로 변수는 그대로 유지된다. 마지막 인덱스까지 비교가 끝났으므로 이제 교환을 할 차례이다. 이번 패스스루의 최솟값 2의 인덱스인 인덱스1과 이번 패스스루의 시작인덱스인 인덱스1이 같은 위치이므로 교환은 일어나지 않고 두 번째 패스스루가 끝난다.
🔵 세 번째 패스스루
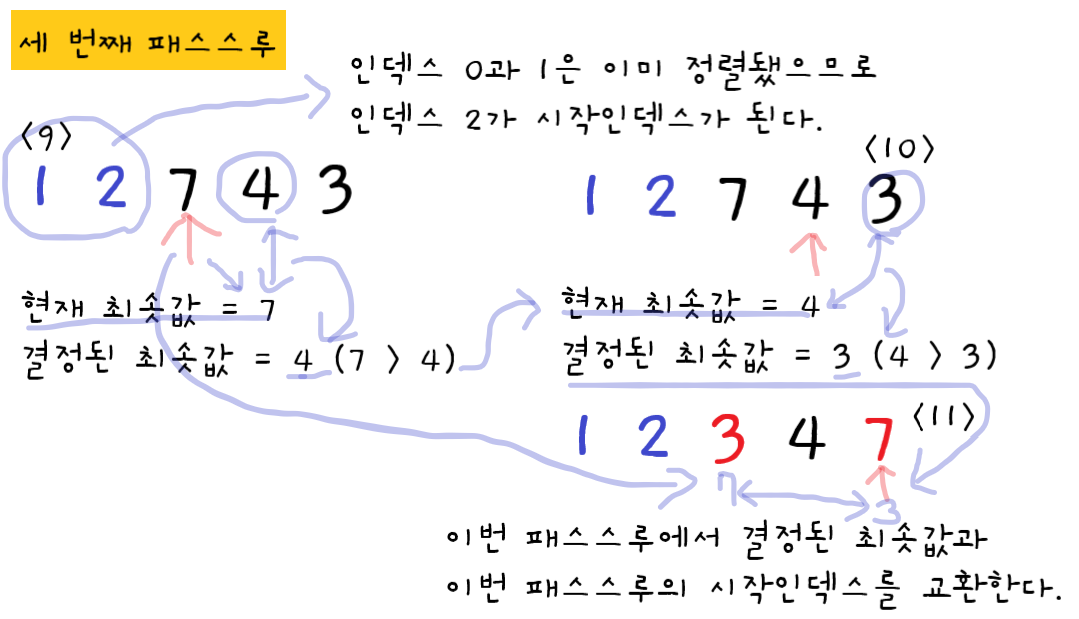
9단계 : 인덱스0과 인덱스1은 이때까지의 패스스루에서 이미 정렬된 값이므로 세 번째 패스스루는 인덱스2가 시작인덱스가 된다. 인덱스2의 값7이 현재 최솟값이므로 이 인덱스를 변수에 저장한다. 현재 최솟값과 오른쪽 값4를 비교하여 결정된 최솟값은 4이므로 변수에 저장되는 값도 7에서 4로 바뀐다.
10단계 : 마지막 인덱스와 비교를 하므로 이 단계에서 정해지는 최솟값이 이번 패스스루의 최솟값이 된다. 현재 최솟값 4와 오른쪽 값 3을 비교한다. 이 때 오른쪽 값이 더 작으므로 결정되는 최솟값은 3이 된다. 변수에 저장되는 값도 4에서 3으로 바뀐다.
11단계 : 마지막 인덱스를 가리키게 되었으니 이번 패스스루의 최솟값과 시작인덱스를 교환하면 패스스루가 종료된다. 이번 패스스루의 최솟값 3의 인덱스인 인덱스4와 이번 패스스루의 시작인덱스인 인덱스2를 교환하고 패스스루는 종료된다. 이번 패스스루로 인하여 이번 패스스루의 시작인덱스까지, 인덱스0부터 인덱스2까지 정렬이 되었다.
🔵 네 번째 패스스루

12단계 : 이때까지의 패스스루에서 인덱스0 ~ 인덱스2까지는 이미 정렬됐으므로 인덱스3이 이번 네 번째 패스스루의 시작인덱스가 된다. 마지막 인덱스와 비교를 하므로 이 단계에서 정해지는 최솟값이 이번 패스스루의 최솟값이 된다. 시작인덱스의 값 4가 현재 최솟값이 된다. 현재 최솟값 4와 다음 인덱스의 값 7을 비교하여 결정된 최솟값은 4가 된다. 이번 패스스루의 최솟값의 인덱스인 인덱스3과 이번 패스스루의 시작인덱스인 인덱스3은 같은 위치이므로 교환이 일어나지 않는다. 그러므로 다음 단계 없이 여기서 패스스루가 끝난다. 이번 패스스루의 시작인덱스(인덱스3)가 배열의 마지막인덱스(인덱스4)의 바로 전 인덱스이므로 이번 패스스루가 마지막 패스스루가 되며 선택정렬이 완전히 종료된다.
❕코드 구현 ❗
- 각 패스스루를 나타내는
for루프를 시작한다.
루프는 변수startIndexOfPassThrough를 통해 배열의 각 인덱스를 가리키며 배열의 마지막인덱스 바로 전까지 살펴본다.
- 변수
lowestNumberIndex에 현재 최솟값의 인덱스를 저장한다.
- 각 패스스루에서는
for루프를 이용해 현재 최솟값과 다음 인덱스를 마지막인덱스까지 비교한다.
(중첩for루프가 된다)
- 각 패스스루에서는 현재최솟값과 다음인덱스의 값을 비교하여 현재 최솟값보다 더 작은 값인지 확인한다. 더 작은 값이라면 변수
lowestNumberIndex를 다음인덱스로 다시 저장한다.
- 패스스루의 최솟값과 패스스루의 시작인덱스를 비교했을 때 같지 않다면 교환한다.
- 끝으로 정렬된 배열을 반환한다.
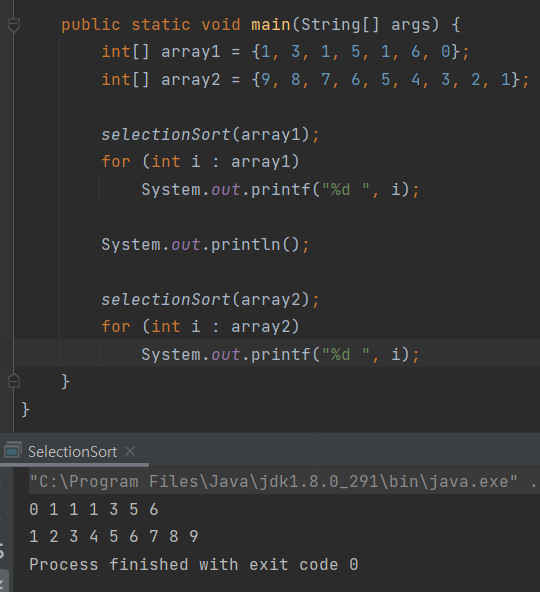
public static int[] selectionSort(int[] array) {
for (int startIndexOfPassThrough = 0; startIndexOfPassThrough < array.length - 1; startIndexOfPassThrough++) {
int lowestNumberIndex = startIndexOfPassThrough;
for (int nextIndex = startIndexOfPassThrough+1; nextIndex < array.length; nextIndex++) {
if (array[nextIndex] < array[lowestNumberIndex])
lowestNumberIndex = nextIndex;
}
if (lowestNumberIndex != startIndexOfPassThrough) {
int temp = array[startIndexOfPassThrough];
array[startIndexOfPassThrough] = array[lowestNumberIndex];
array[lowestNumberIndex] = temp;
}
}
return array;
}main 출력 테스트 통과
🔶 효율성 : O(N²)
선택 정렬은 비교와 교환, 두 종류의 단계를 포함한다.
- 비교 : 각 패스스루 내에서 각 값을 현재까지 찾은 최솟값과 비교한다.
- 교환 : 그렇게 결정된 최종 최솟값을 패스스루의 시작 인덱스와 교환한다.
🔵 {4, 2, 7, 1, 3} 정렬 예제를 보면은


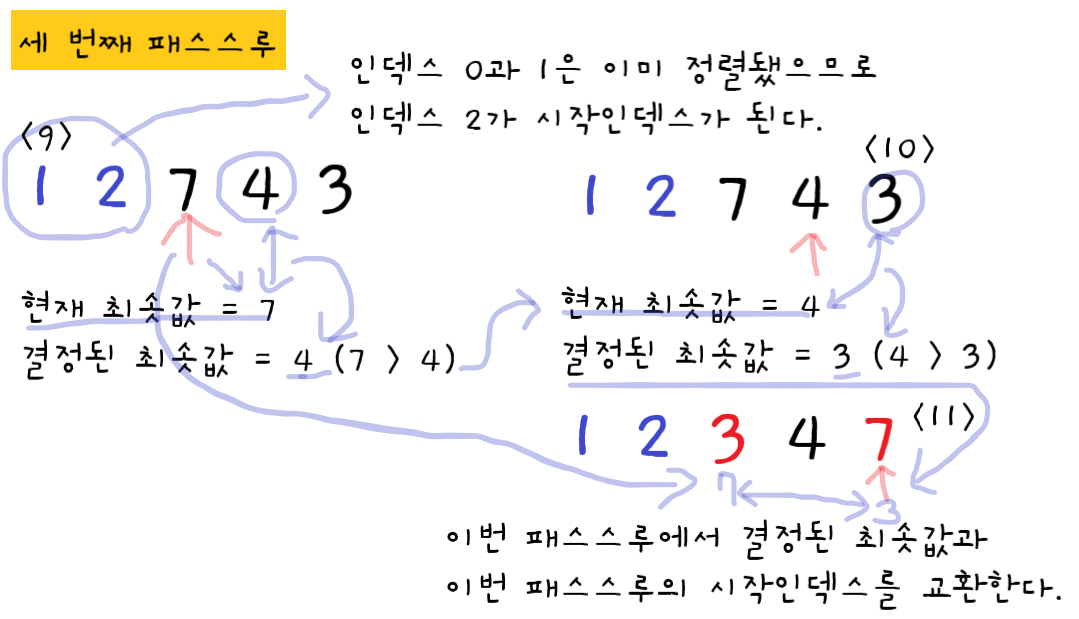

{4, 2, 7, 1, 3} 정렬 예제를 보면은 총 4번의 패스스루에 총 10번의 비교를 교환은 두 번 일어났다.
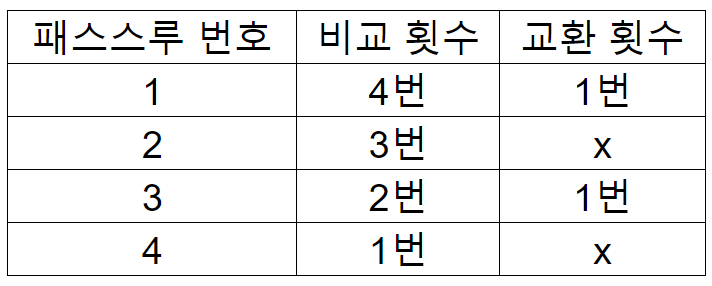
배열의 크기가 5인데 교환은 총 (5 - 1) + (5 - 2) + (5 - 3) + 1 = 10번이 일어났다.
🔵 모든 크기의 배열에 적용되도록 생각해보면은
배열에 원소 N개가 있을 때
- 비교 : (N - 1) + (N - 2) + (N - 3) … + 1
- 교환 : 한 패스스루당 최대 한 번
(배열이 역순으로 정렬된 최악의 시나리오에서는 각 패스스루마다 빠짐없이 교환을 한 번씩 해야한다.)
🔵 버블정렬과 선택정렬의 단계수를 비교하면은
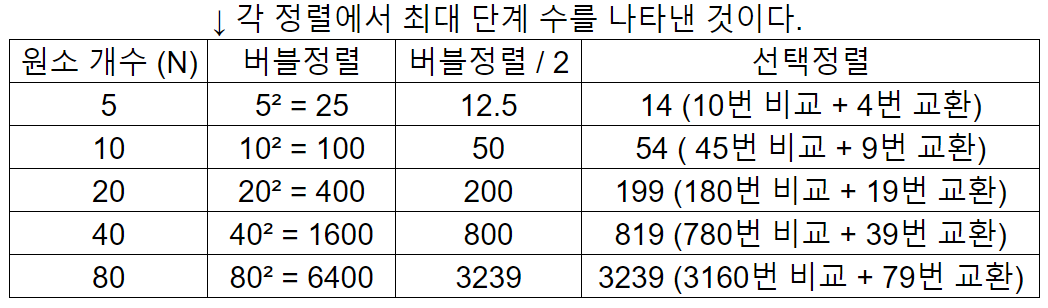
선택정렬은 버블 정렬보다 단계 수가 반 정도(÷2) 적다. 즉, 선택 정렬이 두 배 더 빠르다.
하지만 선택정렬의 효율성은 버블정렬과 똑같이 O(N²)으로 나타낸다. 왜일까? 그 이유는 빅 오의 상수 무시하기 법칙 때문이다.
🟪 빅 오의 <상수 무시하기> 법칙
왜 선택정렬이 버블정렬보다 2배 더 빠름에도 불구하고 빅 오는 똑같이 O(N²)으로 효율성이 표기 되는 걸까?
➡️ 빅오의 상수 무시하기 법칙 때문이다.
빅 오 표기법은 데이터 원소가 N개일 때 얼마나 많은 단계 수가 필요한가라는 질문에 답하는 것이다.
선택 정렬에서는 데이터 원소가 N개일 때 N²/2단계가 걸린다.
선택 정렬은 대략 N²의 반 단계 정도가 걸리므로 O(N²/2)로 효율성을 표기하는 것이 맞는 것 같다.
하지만 선택 정렬의 효율성은 O(N²)이다. 이유는 다음의 빅 오 규칙 때문이다.
❗빅 오 표기법은 상수를 무시한다❗
상수 : 수식에서 변하지 않는 값
↳ N + 2 에서 N은 변하는 값이지만 2는 절대 변하지 않으므로 상수이다.
↳ N/3 + 6에서 N은 그 때 그 때 계속 변하는 값이지만 3과 6은 어떤 상황에서도 절대 변하지 않으므로 상수이다.
❓ 지수가 아닌 수
이해하지 못한 문장들 ↓
빅 오 표기법은 지수가 아닌 수는 포함하지 않는다는 것을 단순히 수학적으로 표현한 문장이다.
표현식에서 이러한 수는 그냥 버린다.
- 지수 : 제곱되는 수를 "밑", 제곱하는 횟수가 "지수"이다.
- 지수가 아닌 수가 상수라는 말인가.....?
오키에 질문해봤다. 답글을 보고 의미를 유추해보면
이러한 빅 오의 상수무시하기 법칙 때문에
N/2단계가 필요한 알고리즘은O(N)으로 표현한다.N²+10단계가 필요한 알고리즘은 지수가 없는10을 버리고O(N²)으로 표현한다.2N단계가 필요한 알고리즘은 상수2를 버리고O(N)으로 표현한다.O(N)보다 100배나 느린O(100N)이라 해도 결국O(N)으 알고리즘 효율성이 표기된다.
빅 오의 상수무시하기 법칙에 의해서 빅 오로는 정확히 똑같이 표현하는 두 알고리즘이지만 실제로는 한쪽이 다른 한쪽보다 100배나 빠를 수도 있다.
이것의 완벽한 예시가 선택 정렬과 버블 정렬이다.
선택 정렬과 버블 정렬이 빅 오로는 O(N²)이지만 실제로는 선택 정렬이 N²/2단계의 알고리즘이고 버블 정렬이 N²단계의 알고리즘이므로 선택정렬이 버블정렬보다 2배 더 빠르다.
여기까지 왜 선택 정렬이 버블 정렬보다 2배 더 빠름에도 불구하고 둘 다 똑같은 빅 오로 표기되는지 알아보았다. → 빅 오의 상수 무시하기 법칙 때문에.
상수무시하기가 무엇인지 이제는 알겠다. 이것때문에 N²/2이나 N²이나 같은 알고리즘 단계수로 표현 되는 것도 이제는 알겠다.
그런데
왜 빅 오는 상수를 무시할까?
➡️ 일반적인 카테고리로만 분류해도 현저한 차이를 나타내기 충분하기 때문이다. 빅 오는 일반적인 카테고리만 나타내기 위한 표기법이기 때문이다.
🟪 빅 오 카테고리 - 상수 무시하기 법칙의 이유
🔶 루프의 실행 횟수에 더 초점을 맞추게 된다.
아래는 주어진 숫자까지의 양의 정수에서 짝수만 찾아내 프린트 하는 함수이다.
public void printEvenNumbers (int upperLimit) {
int number = 2;
while (number <= upperLimit) {
if (number % 2)
System.out.prinln(number);
number++;
}
}upperLimit이 N일 때 루프가 N번 실행되고, 출력은 N과 상관없이 1번 되는 알고리즘이다.
따라서 알고리즘은 O(N+1)이라고 할 수 있고, 이는 상수 무시하기 법칙에 따라 결국엔 O(N)으로 표시된다.
이렇게 상수를 제거함으로써 루프 안에서 정확히 무슨 일이 일어나는지 보다는 실질적으로 루프가 실행되는 횟수에 더 초점을 맞추게 된다.
🔶 건물을 분류하는데 층수까지 표시할 필요는 없다

건물에 비유해서 「빅 오 카테고리」를 설명해보면,
건물의 종류는 매우 다양하다. 고층건물, 상가건물, 아파트, 공장 등등이 있다.
하나는 단독 주택이고 하나는 고층건물인 두 건물을 비교할 때 굳이 각각이 몇 층인지 언급할 이유가 없다.
두 건물의 크기와 기능이 현저히 달라서 "이 건물은 2층짜리 단독주택이고, 저 건물은 100층짜리 고층 건물이다."라고 말 할 필요가 없는 것이다.
그냥 하나는 집이고 하나는 고층 건물이라고 부르면 된다.
🔶 일반적인 카테고리로만 분류해도 현저한 차이를 나타내기 충분하다.
이러한 맥락으로 알고리즘의 효율성 역시 일반적인 카테고리의 알고리즘 속도만 고려하는 것이다.
O(N) 알고리즘과 O(N²) 알고리즘을 비교할 때 두 효율성 간 차이가 너무 커서 O(N)이 실제로 O(2N) 이든 O(N/2) 이든 O(100N) 이든 별로 중요하지가 않는 것이다.
빅 오 표기법은 단지 알고리즘에 필요한 단계 수만 의미하지 않는다. 데이터가 늘어날 때 알고리즘 단계 수가 장기적으로 어떤 궤적을 그리는지가 중요하다.
O(N)은 직선 성장straight growth을 보여준다.
즉 단계 수가 데이터에 일정 비율로 비례해 직선을 그리며 증가한다.
O(N²)은 지수 성장exponential growth의 하나다.
지수 성장은 어떤 형태의 O(N)-직선성장과도 비교되지 않는 완전히 다른 카테고리다.
O(N)에 어떤 수를 곱하든 데이터가 커지다 보면 언젠가 결국 O(N²)이 더 느려지기 때문이다.
O(2N)과 O(N²/50)을 비교하는 것은 2층 주택과 50층 고층건물을 비교하는 것과 다를 바 없다.
간단명료하게 O(N)과 O(N²)으로 비교하면 된다. 단독주택과 고층건물로 두 건물을 비교하면 되는 것과 마찬가지로.
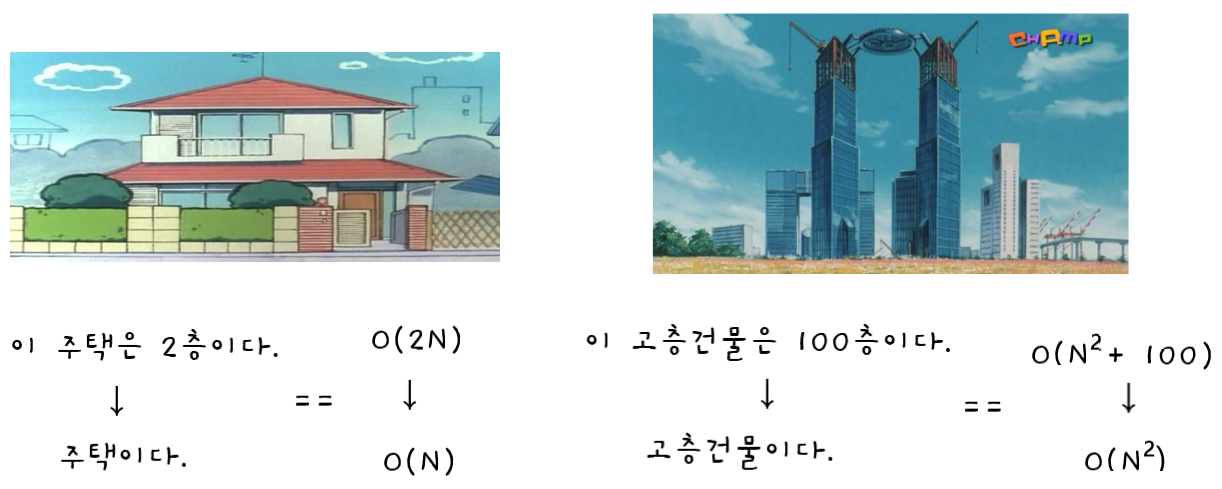
주택끼리, 고층건물끼리 비교하는 것도 아니고
주택과 고층건물 이 두 가지 다른 카테고리를 비교할 때는
주택이 몇 층이고 고층건물이 몇 층인지까지 언급할 필요가 없는 것 처럼
빅 오 또한 서로 다른 카테고리 일 때는 실제 어떤 상수가 곱해져 있고 더해져 있는지 상관없이 카테고리 자체로만 나타내고 비교하면 되는 것이다.
O(139N+11) -> O(N)
그래서 빅 오는 카테고리로만 표기하기 위해서 상수무시하기 법칙이 있는 것이다.
🔶 정리
O(1), O(logN), O(N), O(2N), O(2ⁿ), O(N²) 등과 같은 빅 오 유형은 서로 차이가 큰 일반적인 빅 오 카테고리다.
지수가 아닌 수로 단계 수를 곱하거나 나누거나 더한다고 카테고리가 바뀌지 않는다.
각각의 카테고리 간의 차이가 너무 커서 특정 카테고리에 속하는 어떤 알고리즘이 실제로는O(N²/2)이든O(logN+9)이든 별로 중요하지가 않아진다.
그래서O(N/2)이든O(100N)이든 같은O(N)카테고리로 분류하고,O(4)이든O(1000)이든 같은O(1)카테고리로 분류하는 것이다.그렇기 때문에
빅 오에서 서로 다른 카테고리에 속하는 두 효율성을 비교할 때 일반적인 카테고리로 분류하는 것으로 충분하다.
빅 오 표기법은 일반적인 카테고리의 알고리즘 속도만 고려할 뿐만 아니라.
일반적인 카테고리로만 분류해도 현저한 차이를 나타내기 충분하기 때문이다.그렇기 때문에
빅오의 상수무시하기 법칙이 있는 것이다.
🔶 두 알고리즘이 같은 카테고리에 속할 때는
하지만 두 알고리즘이 같은 카테고리에 속하더라도 서로 처리 속도가 다를 수 있다.
앞에서 계속 예시로 들었듯이 버블 정렬과 선택 정렬은 둘 다 같은 O(N²) 카테고리에 속하지만 실제로 더욱 깊게 비교해보면 버블 정렬은 선택 정렬보다 두 배 느리다.
따라서 빅오에서 서로 다른 카테고리에 속하는 알고리즘을 대조할 때는 빅 오가 완벽한 도구지만 같은 카테고리에 속하는 두 알고리즘이라면 어떤 알고리즘이 더 빠를지 알기 위해 더 분석 해야 한다.
🟪 함수의 효율성 맞춰보기
🔵 1.
주어진 배열의 모든 수를 두 배로 만든 후 그 합을 반환하는 함수
public int doubleThenSum (int[] array) {
int[] doubledArray = new int[array.length];
int sum = 0;
for (int idx = 0; idx < array.length; idx++) {
doubledArray[idx] = array[idx] * 2;
}
for (int num : doubledArray)
sum += num;
return sum;
}: array의 원소 갯수가 N일 때 2개의 for루프가 모두 각각 N번씩 수행되므로 O(2N) ➡️ O(N)이다.
🔵 2.
문자열 배열을 받아 각 문자열을 다양한 형태로 출력하는 함수
public void multipleCases (String[] array) {
for (String str : array) {
System.out.println(str.toLowerCase());
System.out.println(str.toUpperCase());
System.out.println(str.substring(0,1).toUpperCase() + str.substring(1));
}
}: array의 원소 갯수가 N일 때 출력이 3번씩 N번(for루프) 수행되므로 O(3N) ➡️ O(N)이다.
🔵 3.
주어진 배열의 인덱스가 짝수이면 배열 내 모든 수에 대해 그 인덱스의 수를 더해 출력하는 함수
public void everyOther(int[] array) {
for (int idx = 0; idx < array.length; idx++) {
if (idx % 2 == 0) {
for (int num : array)
System.out.println(num + idx);
}
}
}: array의 원소 갯수가 N일 때 출력이 N번씩 N/2번(중첩 for루프) 수행되므로 O(N²/2) ➡️ O(N²)이다.
🟦 출처
🔷 그림1

123RF사이트에서 marcopolo님의 에스프레소에서 현대적인 고층 건물에 이르기까지 다양한 종류의 건물게시물을 확인해보세요
🔷 글의 내용
이 글 내용은 '제인 웬그로우'의 '누구나 자료구조와 알고리즘 개정 2판' 책을 100% 참고하여 작성하였습니다. 설명에 전문적인 용어보다는 일상적인 용어를 사용하고 그림으로 원리를 설명해주어 왕초보인 저가 이해하기에 아주 좋았습니다. 가격이 많이 나가는 편이지만 꼭 배워야 하는 내용이 모두 들어있고 그것을 제가 이해할 수 있는 수준으로 쓰여있어 전혀 아깝지 않은 소비였습니다.



