🟪 정렬 알고리즘

정렬되지 않은 배열이 주어졌을 때, 어떻게 오름차순/내림차순으로 정렬할 수 있을까?

정렬 알고리즘은 컴퓨터 과학 분야에서 폭넓게 연구된 주제이며, 지난 수년간 수십 개의 정렬 알고리즘이 개발돼 왔다. 이러한 알고리즘 모두 "정렬되지 않은 배열이 주어졌을 때, 어떻게 오름차순/내림차순으로 정렬할 수 있을까?"라는 문제를 해결한다.

버블 정렬, 힙 정렬, 퀵 정렬, 트리 정렬 등 모두 정렬 알고리즘 중 하나이다.

🟪 🌟버블 정렬🌟

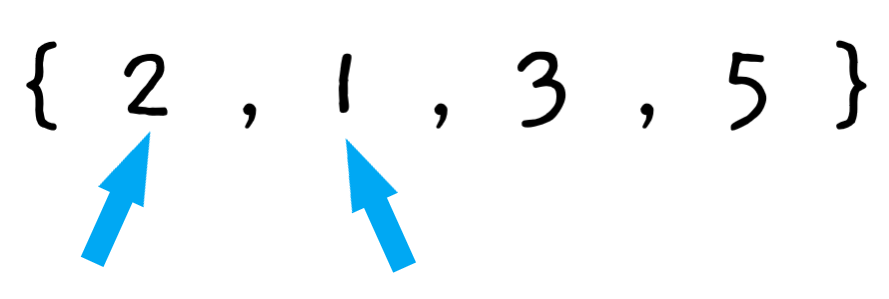
1단계 : 배열 내 연속된 두 항목을 비교한다.
처음에는 배열의 첫 번째 원소부터 시작하므로 첫 번째 항목과 두 번째 항목을 비교한다.

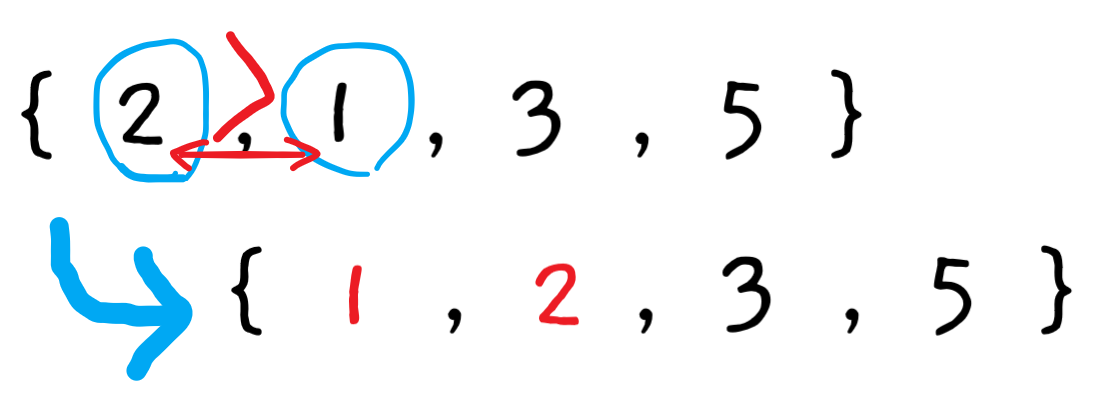
2단계 : 왼쪽 값이 오른쪽 값보다 크면 두 항목을 교환swap한다.
만약 순서가 올바르다면 아무것도 하지 않고 그 다음 항목으로 넘어간다.

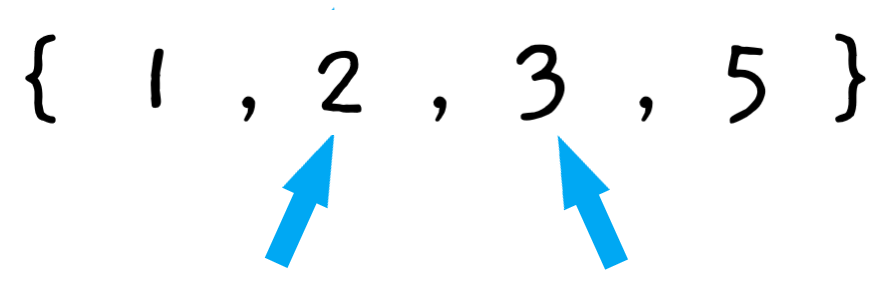
3단계 : "포인터"를 오른쪽으로 한 셀씩 옮긴다.

4단계 : 배열의 끝까지 또는 이미 정렬된 값까지 1단계부터 3단계를 반복한다. ➡️ 이미 정렬된 값 : 각 패스스루마다 정렬되지 않은 값 중 가장 큰 값 "버블"이 올바른 위치로 가게 된다.

이것이 배열의 첫 패스스루pass-through가 끝난 것이다.
즉 배열 끝까지(정렬된 값까지) 값을 하나하나 가리키며 배열을 "통과"한 것이다.

5단계 : 이제 두 포인터를 다시 배열의 처음 두 값으로 옮겨서 1단계부터 4단계를 다시 실행함으로써 새로운 패스스루를 실행한다.
교환이 일어나지 않는 패스스루가 생길 때까지 반복한다. ➡️ 패스스루에서 교환이 한 번이라도 수행되었다면 다음 패스스루도 수행해야 한다.
교환할 항목이 없다는 것은 배열이 완전히 정렬됐다는 뜻이다.

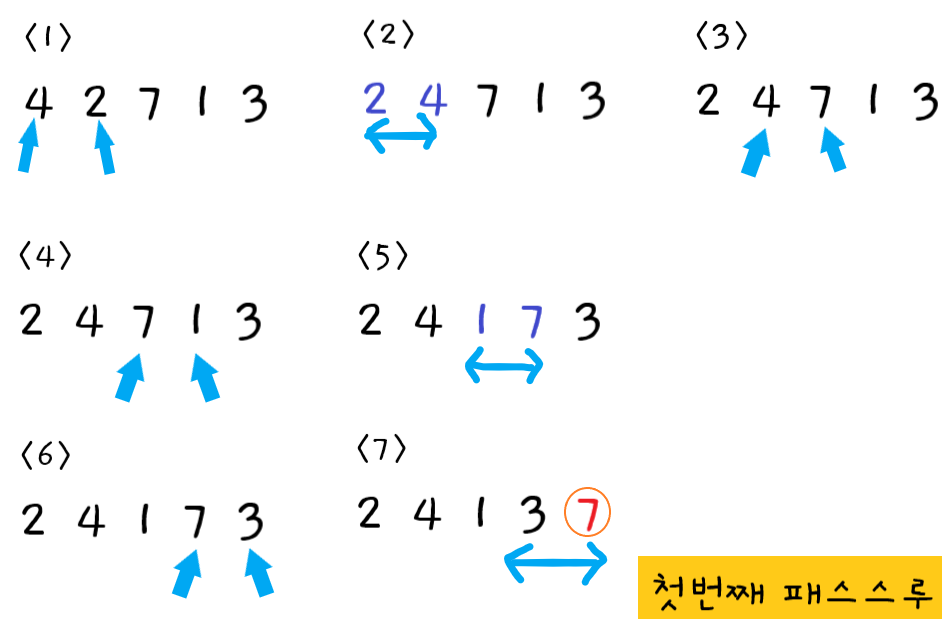
🔵 {4, 2, 7, 1, 3} 정렬 해보기

• 첫 번째 패스스루

  • 1단계 : 먼저 4와 2를 비교한다.

  • 2단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

  • 3단계 : 다음으로 4와 7를 비교한다. 순서가 올바르므로 교환하지 않고 다음 포인터로 넘어간다.

  • 4단계 : 다음으로 7와 1를 비교한다.

  • 5단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

  • 6단계 : 다음으로 7와 3를 비교한다.

  • 7단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

첫 번째 패스스루가 끝났으므로 정렬되지 않은 값 중 가장 큰 값 "버블7"이 확실히 올바른 위치에 있게 되었다.

이번 패스스루에서 교환을 한 번 이상 하였으므로 다음 패스스루도 수행해야 한다.

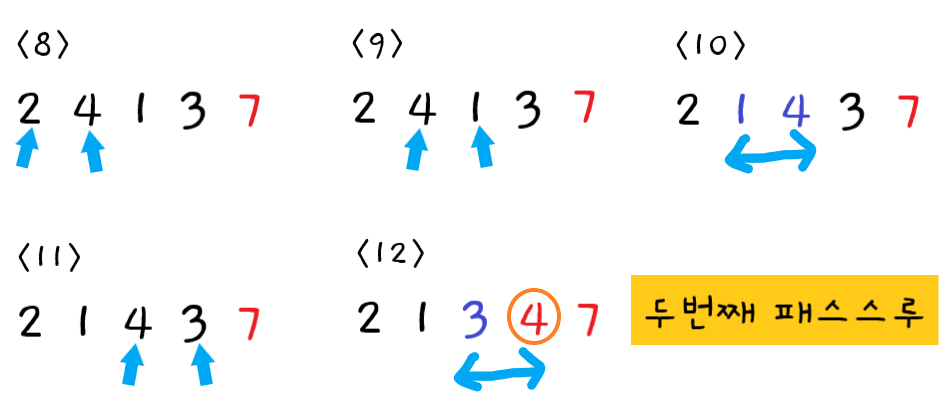
• 두 번째 패스스루

  • 8단계 : 먼저 2와 4를 비교한다. 순서가 올바르므로 교환하지 않고 다음 포인터로 넘어간다.

  • 9단계 : 다음으로 4와 1를 비교한다.

  • 10단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

  • 11단계 : 다음으로 4와 3를 비교한다.

  • 12단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

첫 번째 패스스루로 인해 7이 올바른 위치에 있으므로 4와 7은 비교할 필요가 없다.

두 번째 패스스루가 끝났으므로 정렬되지 않은 값 중 가장 큰 값 "버블4"가 확실히 올바른 위치에 있게 되었다.

이번 패스스루에서 교환을 한 번 이상 하였으므로 다음 패스스루도 수행해야 한다.

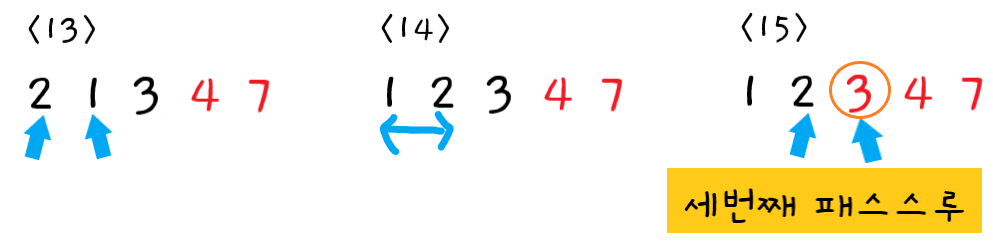
• 세 번째 패스스루

  • 13단계 : 먼저 2와 1를 비교한다.

  • 14단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

  • 15단계 : 다음으로 2와 3를 비교한다. 순서가 올바르므로 교환하지 않는다.

이때까지의 패스스루로 인해 4와 7이 올바른 위치에 있으므로 3과 4는 비교할 필요가 없다.

세 번째 패스스루가 끝났으므로 정렬되지 않은 값 중 가장 큰 값 "버블3"이 확실히 올바른 위치에 있게 되었다.

이번 패스스루에서 교환을 한 번 이상 하였으므로 다음 패스스루도 수행해야 한다.

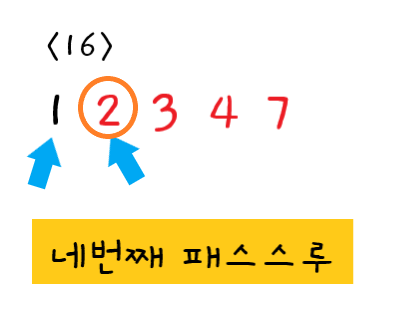
• 네 번째 패스스루

  • 16단계 : 먼저 1와 2를 비교한다. 순서가 올바르므로 교환하지 않는다.

이때까지의 패스스루로 인해 3과 4와 7이 올바른 위치에 있으므로 2와 3은 비교할 필요가 없다.

네 번째 패스스루가 끝났으므로 정렬되지 않은 값 중 가장 큰 값 "버블2"가 확실히 올바른 위치에 있게 되었다.

이번 패스스루에서는 어떤 교환도 하지 않았으므로 패스스루를 더 이상 수행하지 않고 종료한다. 이제 이 배열은 완전히 정렬되었다.

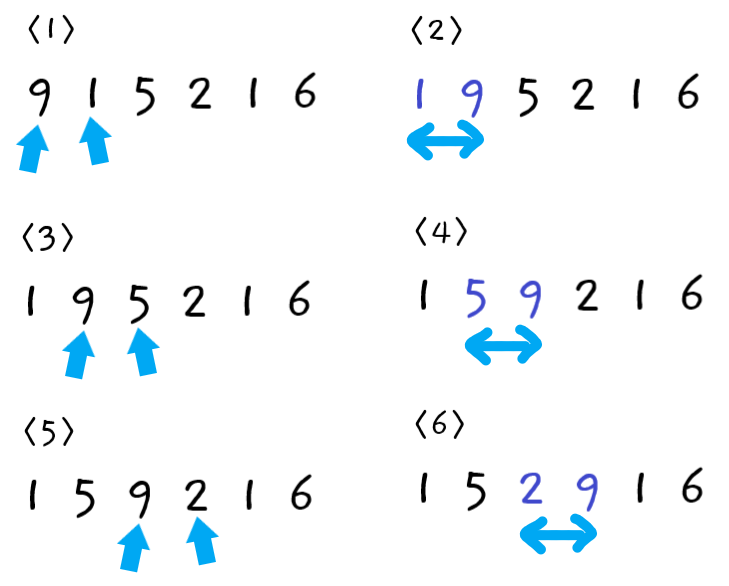
🔵 {9, 1, 5, 2, 1, 6} 정렬 해보기

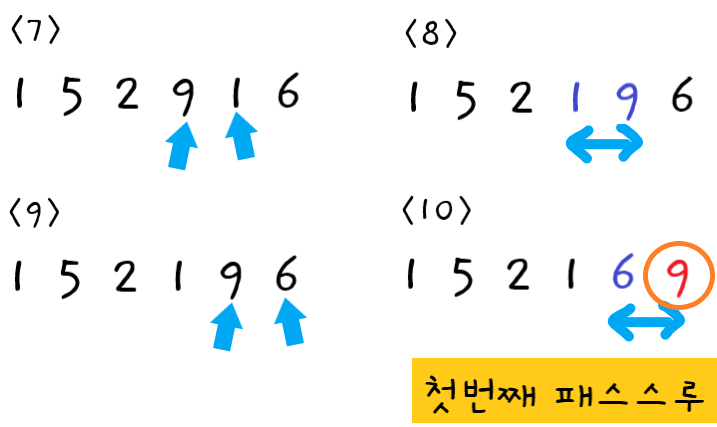
• 첫 번째 패스스루

  • 1단계 : 먼저 9와 1을 비교한다.

  • 2단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

  • 3단계 : 다음으로 9와 5를 비교한다.

  • 4단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

  • 5단계 : 다음으로 9와 2를 비교한다.

  • 6단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

  • 7단계 : 다음으로 9와 1를 비교한다.

  • 8단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

  • 9단계 : 다음으로 9와 6를 비교한다.

  • 10단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

첫 번째 패스스루가 끝났으므로 정렬되지 않은 값 중 가장 큰 값 "버블9"가 확실히 올바른 위치에 있게 되었다.

이번 패스스루에서 교환을 한 번 이상 하였으므로 다음 패스스루도 수행해야 한다.

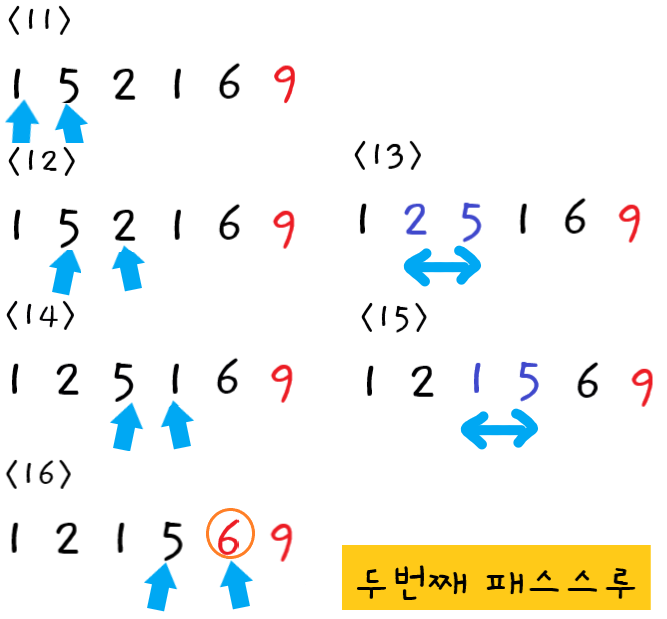
• 두 번째 패스스루

  • 11단계 : 먼저 1과 5를 비교한다. 순서가 올바르므로 교환하지 않고 다음 포인터로 넘어간다.

  • 12단계 : 다음으로 5와 2를 비교한다.

  • 13단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

  • 14단계 : 다음으로 5와 1을 비교한다.

  • 15단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

  • 16단계 : 다음으로 5와 6을 비교한다. 순서가 올바르므로 교환하지 않는다.

첫 번째 패스스루로 인해 9가 올바른 위치에 있으므로 6과 9는 비교할 필요가 없다.

두 번째 패스스루가 끝났으므로 정렬되지 않은 값 중 가장 큰 값 "버블6"이 확실히 올바른 위치에 있게 되었다.

이번 패스스루에서 교환을 한 번 이상 하였으므로 다음 패스스루도 수행해야 한다.

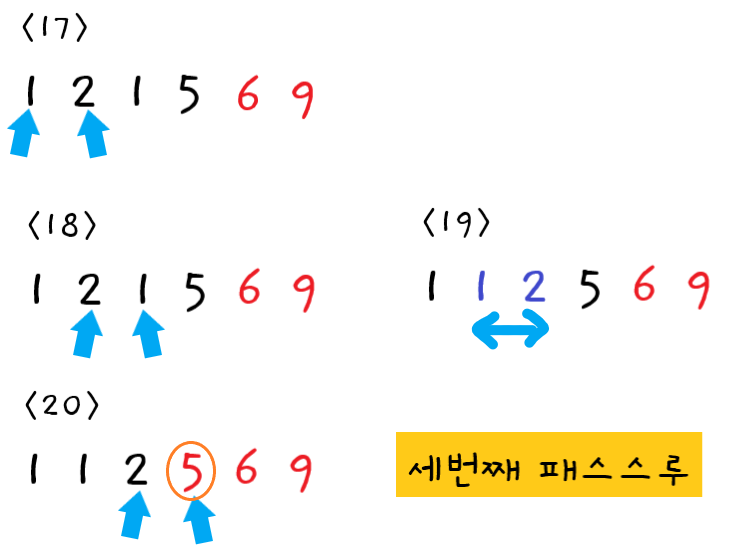
• 세 번째 패스스루

  • 17단계 : 먼저 1과 2를 비교한다. 순서가 올바르므로 교환하지 않고 다음 포인터로 넘어간다.

  • 18단계 : 다음으로 2와 1을 비교한다.

  • 19단계 : 왼쪽값 > 오른쪽값 이므로 둘을 교환한다.

  • 20단계 : 다음으로 2와 5를 비교한다. 순서가 올바르므로 교환하지 않는다.

이때까지의 패스스루로 인해 6과 9가 올바른 위치에 있으므로 5와 6은 비교할 필요가 없다.

세 번째 패스스루가 끝났으므로 정렬되지 않은 값 중 가장 큰 값 "버블5"가 확실히 올바른 위치에 있게 되었다.

이번 패스스루에서 교환을 한 번 이상 하였으므로 다음 패스스루도 수행해야 한다.

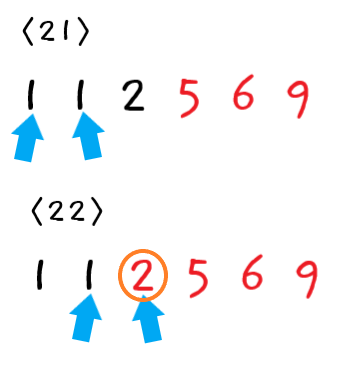
• 네 번째 패스스루

  • 21단계 : 먼저 1과 1을 비교한다. 순서가 올바르므로 교환하지 않는다.

  • 22단계 : 다음으로 1과 2를 비교한다. 순서가 올바르므로 교환하지 않는다.

이때까지의 패스스루로 인해 5와 6과 9가 올바른 위치에 있으므로 2와 5는 비교할 필요가 없다.

네 번째 패스스루가 끝났으므로 정렬되지 않은 값 중 가장 큰 값 "버블2"가 확실히 올바른 위치에 있게 되었다.

이번 패스스루에서는 어떤 교환도 하지 않았으므로 패스스루를 더 이상 수행하지 않고 종료한다. 이제 이 배열은 완전히 정렬되었다.

❕코드 구현 ❗

• 함수는 정렬되지 않은 배열을 전달하여 사용한다.

• 그러면 함수는 정렬된 배열을 반환한다.

• unsortedUntilIndex 변수 : 아직 정렬되지 않은 배열의 가장 오른쪽 인덱스를 기록한다.
  ( 알고리즘이 처음 시작할 때는 전체 배열의 마지막 인덱스로 변수를 초기화한다. )

• sorted 변수 : 배열의 정렬 여부를 기록한다.
  (알고리즘이 처음 시작할 때는 정렬되지 않았으므로 false로 초기화한다.)

• while루프
  • 배열이 정렬될 때까지 실행한다.
    ↳ while (!sorted) {}
  • 루프 한 번 실행이 배열의 한 패스스루에 해당한다.

⬇️ 루프안에서

• 각 패스스루 안에서는 교환이 일어나기 전까지 배열이 정렬되어 있다고 가정하고 교환이 일어났을 때 다시 false로 바꾸는 방식을 취한다.
  ↳ sorted = true;

• for루프 : 배열 내 모든 값 쌍을 가리킨다. i를 첫 포인터로 사용해 배열의 첫 인덱스부터 아직 정렬되지 않은 인덱스까지 수행한다.
  ↳ for(int pointer = 0; pointer < unsortedUntilIndex; pointer++) {}
  • for루프 내에서는 모든 인접 값 쌍을 비교하고 왼쪽값 > 오른쪽값이면 교환한다. ➡️ 교환이 일어났으므로 sorted = false

• 각 패스스루가 끝나면 버블이 이제 올바른 위치에 있게 된다. 즉 unsortedUntilIndex변수가 기존에 가리키고 있던 인덱스가 정렬된 상태이니 unsortedUntilIndex변수의 값을 1 감소 시킨다.

• sorted변수가 true인 채로 패스스루가 끝나면 while루프가 종료된다. 이 때 정렬된 배열을 반환한다.

public static ArrayList<Integer> bubbleSort(ArrayList<Integer> list) {
    int unsortedUntilIndex = list.size() - 1;
    boolean sorted = false;

    while (!sorted) {
        sorted = true;

        for (int pointer = 0; pointer < unsortedUntilIndex; pointer++) {
            int thisValue = list.get(pointer);
            int nextValue = list.get(pointer+1);
            if (thisValue > nextValue) {
                list.set(pointer, nextValue);
                list.set(pointer+1, thisValue);
                sorted = false;
            }
        }

        unsortedUntilIndex--;
    }

    return list;
}

• main 출력 테스트 통과!

public static void main(String[] args) {
    ArrayList<Integer> list1 = new ArrayList<>(Arrays.asList(4, 2, 7, 1, 3));
    ArrayList<Integer> list2 = new ArrayList<>(Arrays.asList(9, 1, 5, 2, 1, 6));

    bubbleSort(list1);
    for (int i : list1)
        System.out.print(i +" ");

    System.out.println("\n --------");

    bubbleSort(list2);
    for (int i : list2)
        System.out.print(i +" ");
}

🔶 효율성 : O(N²)

버블 정렬 알고리즘은 비교comparison과 교환swap의 두 가지 단계를 포함한다.

원소가 5개인 정렬되지 않은 배열을 생각해보자.

• 비교 comparison

  • 첫 번째 패스스루에서는 비교를 4번 일어난다.

  • 두 번째 패스스루에서는 비교를 3번 일어난다.

  • 세 번째 패스스루에서는 비교를 2번 일어난다.

  • 네 번째 패스스루에서는 비교를 1번 일어난다.

  • 총 10번의 비교다.

  ➡️ 배열의 원소가 N개일 때, (N-1) + (N-2) + (N-3) + … + 1 번의 "비교"를 수행한다.

• 교환 swap

  • 배열이 역순으로 정렬된 최악의 시나리오라면 비교할 때마다 교환을 해야한다.

  • 첫 번째 패스스루에서는 비교를 4번 했으니 교환도 4번 일어난다.

  • 두 번째 패스스루에서는 비교를 3번 했으니 교환도 3번 일어난다.

  • 세 번째 패스스루에서는 비교를 2번 했으니 교환도 2번 일어난다.

  • 네 번째 패스스루에서는 비교를 1번 했으니 교환도 1번 일어난다.

  • 총 10번의 교환이다.

  ➡️ 배열의 원소가 N개일 때, (N-1) + (N-2) + (N-3) + … + 1 번의 "교환"을 수행한다.

원소 5개가 역순으로 된 배열에서는 4+3+2+1 = 10번의 비교와 4+3+2+1 = 10번의 교환이 일어나므로 총 20단계다.

원소 10개가 역순으로 된 배열에서는 9+8+7+6+5+4+3+2+1 = 45번의 비교와 45번의 교환이 일어나므로 총 90단계다.

원소 20개가 역순으로 된 배열에서는 19 + 18 + 17 + 16 + 15 + 14 + 13 + 12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 190번의 비교와 교환이 일어나므로 총 380단계다.

원소 수가 증가할수록 단계 수가 기하급수적으로 늘어난다.

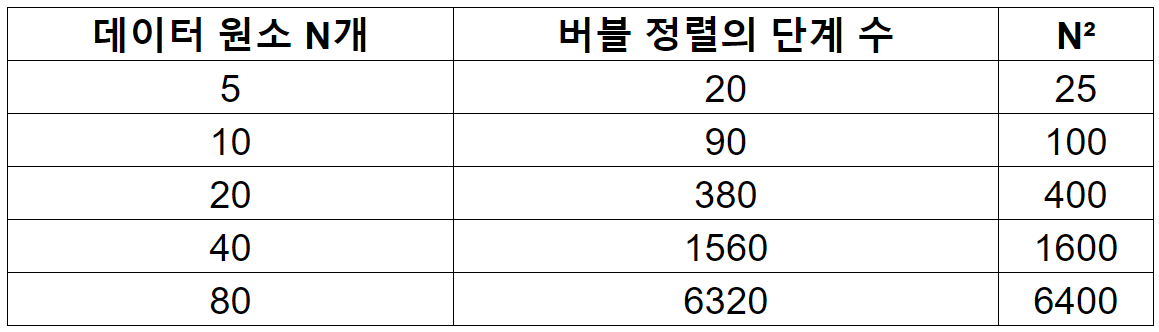
N이 증가할 때마다 단계 수가 대략 N²만큼 늘어남을 알 수 있다.

배열의 원소가 N개일 때 버블 정렬에는 N²단계가 필요하다. ➡️ O(N²)

🟪 O(N²)

🔶 버블정렬과 중첩루프

버블정렬과 중첩루프가 대표적인 O(N²)알고리즘의 예시이다.

버블정렬을 살펴보았고 중첩루프의 예시를 들겠다.

🔵 중첩루프 예시

주어진 배열의 모든 숫자 쌍의 최대곱the greatest product을 찾는다.

public static int greatestProduct(int[] array) {
    int greatestProduct = array[0] * array[1];

    for (int i = 0; i < array.length; i++) {
        for (int j = 0; j < array.length; j++) {
            int nowProduct = array[i] * array [j];
            if (i != j && ( nowProduct > greatestProduct))
                greatestProduct = nowProduct;
        }
    }

    return greatestProduct;
}

🔶 이차시간

O(N²)을 이차시간quadratic time 이라고도 부른다.

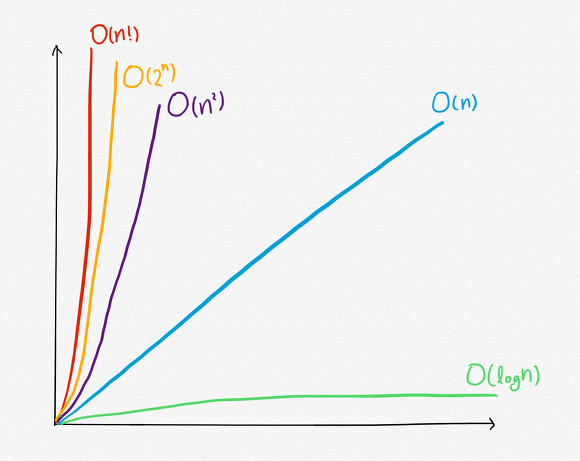
🔶 O(N²) vs O(N) 그래프

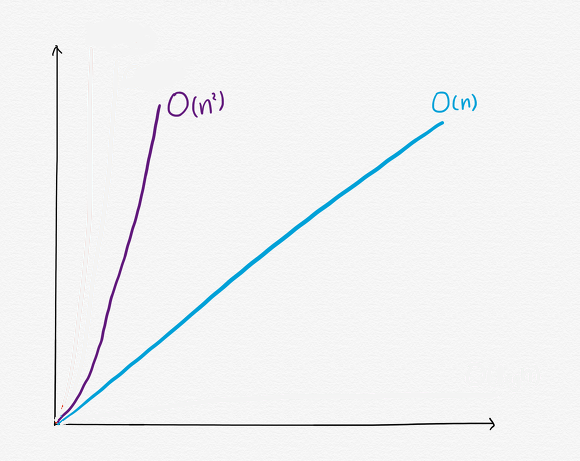
단순한 대각선을 그리는 O(N)과 대비되게 데이터가 늘어날수록 O(N²)의 단계 수가 매우 급격히 증가하고 있다. 그래서 O(N²)은 비효율적인 알고리즘으로 분류된다.

🔶 이차 문제

느린 O(N²) 알고리즘을 빠른 O(N) 알고리즘으로 대체하고자 하는 것을 이차문제라고 한다.

🔵 중첩루프 문제와 선형 해결법

루프 내에 다른 루프를 중첩하는 알고리즘은 O(N²)이다.
(항상은 아니다.)

O(N²)은 상대적으로 느린 알고리즘이다.

느린 알고리즘을 마주할 때는 시간을 들여 더 빠른 속도의 알고리즘 대안은 없을 지 고민해 보는 것이 좋다.

대안 중 하나로 선형 해결법을 고려해볼 수 있다.

선형 해결법은 중첩 루프를 쓰지 않는 것을 의미한다.

🟪 이차문제 연습

🔶 중복 값 확인하는 함수

( 사용자가 제품에 대해 1부터 10사이로 매긴 평점을 분석하는 애플리케이션에서 평점 ) 배열에 중복 숫자가 들어 있는지 확인하는 함수

예를 들어 배열 { 1, 5, 3, 9, 1, 4 } 에는 숫자 1이 중복되므로 true를 반환한다.

🔵 중첩루프로 구현한다. ➡️ O(N²)

: 함수는 반복해서 i와 j를 비교한다. 최악의 시나리오는 배열에 중복 값이 없는 경우다. 배열에 N개가 있을 때 함수는 N²번의 비교를 수행한다. ➡️ O(N²)

public static boolean hasDuplicateValue(int[] array) {
    for (int i = 0; i < array.length; i++) {
        for (int j = 0; j <array.length; j++) {
            if (i != j && array[i] == array[j])
                return true;
        }
    }
    return false;
}

🔵 선형해결법으로 구현한다. ➡️ O(N)

: 단 하나의 루프에서 단지 배열에 있는 원소 수만큼 순회하기 때문에 배열에 N개의 원소가 있을 때 N단계가 걸린다. ➡️ O(N)

• JS 코드
  • existingNumbers라는 빈 배열을 생성한다.
  • for루프를 사용해 array의 각 숫자를 확인한다.
  • 숫자가 나올 때마다 existingNumbers배열에 그 숫자 해당하는 인덱스에 임의의 값 1을 넣는다.
    • 예시) {3, 5, 8}배열에서 3이 나오면 existingNumbers배열의 인덱스3에 1을 대입한다.
    • 그러면 existingNumbers배열은 이렇게 된다.
      : { null , null , null , 1 }
  • 본질적으로 existingNumbers의 인덱스를 사용해 지금까지 array에서 어떤 숫자들이 나왔는지 알 수 있다.
  • 해당 인덱스에 1을 저장하기 전에 이 인덱스의 값이 이미 1인지 확인한다.
  • 해당 인덱스의 값이 1이면, 중복값이라는 뜻이므로 true를 반환한다.
  • 루프 끝까지 갔다면 중복 값이 없다는 뜻이므로 false를 반환한다.

function hasDuplicateValue(array) {
  let existingNumbers = [];
  
  for(let i = 0; i < array.length; i++) {
    if(existingNumbers[array[i]] === 1)
      return true;
    else
      existingNumbers[array[i]] = 1;
  }
  
  return false;
}

• Java 코드
  • existingNumbers라는 ArrayList을 생성한다.
  • ❗ArrayList는 리스트의 끝으로만 추가할 수 있기 때문에,
    array의 값을 인덱스로 하여 임의의 값 1을 추가 할 수 없다.
    • {3,5,8}에서 ArrayList.add(3, 1)이렇게 하면
      (인덱스는 {3,5,8}의 3, 값은 임의의 값 1)
      IndexOutOfBoundsException: Index: 3, Size: 0라는 에러가 뜬다.
    • 그래서 그냥 array의 값을 넣는 식으로 해야한다.
    • {3,5,8}에서 ArrayList.add(3)이런 식으로.
  • for루프를 사용해 array의 각 숫자를 확인한다.
  • 숫자가 나올 때마다 existingNumbers배열에 그 숫자를 추가add()한다.
    • 예시) {3, 5, 8}배열에서 3이 나오면 existingNumbers배열에 3을 대입한다.
      : existingNumbers.add(3)
    • 그러면 existingNumbers배열은 이렇게 된다.
      : { 3 }
  • 해당 값을 ArrayList에 저장하기 전에 이미 있는 값인지 확인한다. 있으면 true를 반환한다.
    : existingNumbers.contains(3)
  • 루프 끝까지 갔다면 중복 값이 없다는 뜻이므로 false를 반환한다.

public static boolean hasDuplicateValue2(int[] array) {
    ArrayList<Integer> existingNumbers = new ArrayList<>();

    for (int value : array) {
        if (existingNumbers.contains(value))
            return true;
        else
            existingNumbers.add(value);
    }

    return false;
}

🔶 최댓값 찾는 함수

배열에서 가장 큰 수를 찾는 함수이다.

🔵 중첩루프로 구현한다. ➡️ O(N²)

• 우선 첫번째 for루프로 나오는 숫자가 제일 크다고 가정한다
  : isNumber1GreatestNumber = true
• 첫번째 for루프로 나오는 숫자가 두번째 for루프로 나오는 숫자보다 작으면 제일 큰 값이 아니게 된다.
  : isNumber1GreatestNumber = false
• 첫번째 for루프로 나오는 숫자가 두번째 for루프로 나오는 숫자들 모두 확인했는데도 제일 크면, 전체 배열에서 가장 큰 수 이므로 return한다.
• java에서는 if문에서 return하면 else문 또는 메소드 자체에서 return값이 있어야 하므로 int failResult = 0;을 선언하여 마지막에 return failResult;한다.

public static int greatestNumber(int[] array) {
    int failResult = 0;
    for (int number1 : array) {
        boolean isNumber1GreatestNumber = true;
        for (int number2 : array) {
            if (number1 < number2)
                isNumber1GreatestNumber = false;
        }
        if (isNumber1GreatestNumber)
            return number1;
    }
    return failResult;
}

🔵 선형해결법으로 구현한다. ➡️ O(N)

• greatestNumber을 임의로 정해서 for루프로 나오는 숫자들과 비교하여 결과에 맞춰 greatestNumber값을 계속 바꾸다가 마지막에 return한다.

public static int greatestNumber2(int[] array) {
    int greatestNumber = array[0];
    
    for (int number : array) {
        if (number > greatestNumber)
            greatestNumber = number;
    }
    
    return greatestNumber;
}

---

🟦 출처

🔷 그림 1

티스토리 사이트의 베카의에러뿌시기 블로그의 '빅오표기법(Big O notation)' 게시글 보러가기

🔷 글의 내용

이 글 내용은 '제인 웬그로우'의 '누구나 자료구조와 알고리즘 개정 2판' 책을 100% 참고하여 작성하였습니다. 설명에 전문적인 용어보다는 일상적인 용어를 사용하고 그림으로 원리를 설명해주어 왕초보인 저가 이해하기에 아주 좋았습니다. 가격이 많이 나가는 편이지만 꼭 배워야 하는 내용이 모두 들어있고 그것을 제가 이해할 수 있는 수준으로 쓰여있어 전혀 아깝지 않은 소비였습니다.

🖱 클릭! | '제인 웬그로우'의 '누구나 자료구조와 알고리즘' 책 구경하러 가보기