
🟪 배열
✔️ 자료구조
✔️ 데이터 원소들의 단순한 리스트
배열은 컴퓨터 과학에서 기초적인 자료 구조 중 하나예요. 배열은 데이터 원소들의 단순한 리스트입니다.
🔶 배열의 크기
배열의 크기는 배열에 데이터 원소가 얼마나 들어있는지 알려준다.
배열의 크기를 보면 배열에 데이터 원소가 얼마나 들어있는지 알 수 있어요.
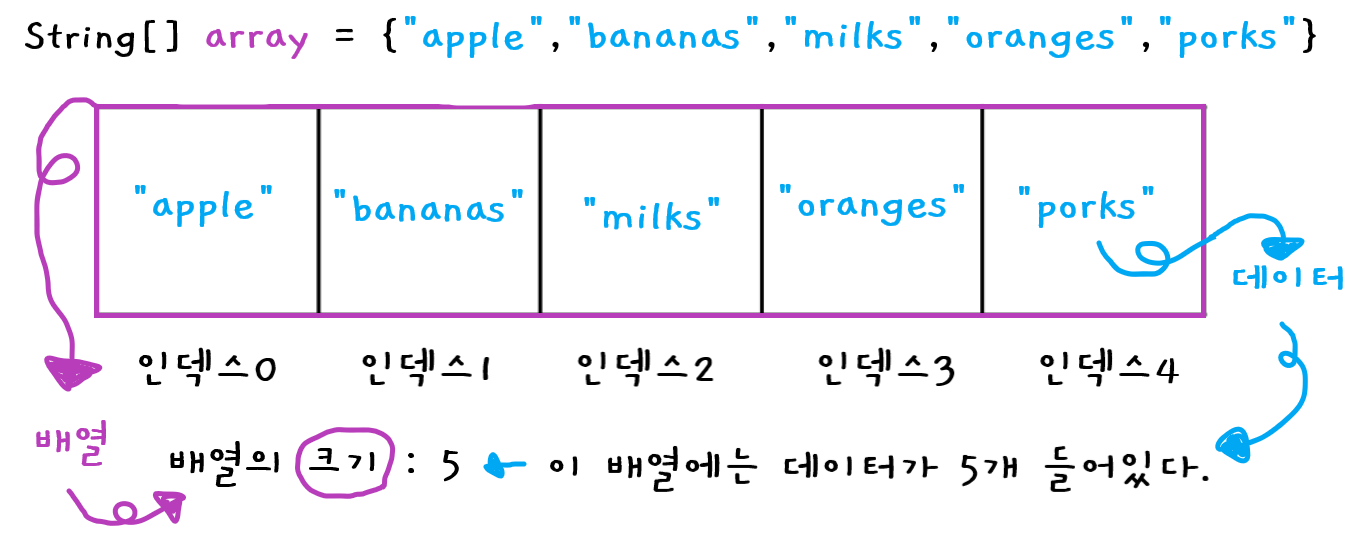
String[] array = {"apple", "bananas", "milks", "oranges", "porks"}
⬆️한개 ⬆️두개 ⬆️세개 ⬆️네개 ⬆️다섯개
✔️ 총 다섯개의 값이 들어있으므로
✔️ 배열의 크기 = 5예를 들어 이 배열에는 값이 5개가 들어있으니 배열의 크기는 크기가 5입니다.
🔶 배열의 인덱스
배열의 인덱스는 특정 데이터가 배열의 어디에 있는지 알려준다. 보통 인덱스는 0부터 시작한다.
배열의 인덱스는 특정 데이터가 배열의 어디에 있는지 알려주는 숫자입니다. 대부분의 프로그래밍 언어에서 인덱스는 0부터 시작해요.
String[] array = {"apple", "bananas", "milks", "oranges", "porks"}
⬆️인덱스0 ⬆️인덱스1 ⬆️인덱스2 ⬆️인덱스3 ⬆️인덱스4
✔️ 데이터 "apple"은 인덱스0에 있다.
✔️ 데이터 "milks"는 인덱스 2에 있다.예를 들어 이 배열에 들어있는 5개의 데이터 중에서 "porks"라는 데이터는 배열의 인덱스4에 있다. "bananas"라는 데이터는 배열의 인덱스1에 있다.
🟪 집합

집합은 중복 값을 허용하지 않는 자료구조다.
집합은 중복 데이터가 없어야 할 때 유용한 자료구조다.
중복된 값이 전혀 없어야 하는 전화번호부가 좋은 예시이다.
집합의 종류는 꽤 다양하지만 여기서는 배열 기반 집합을 다룹니다.배열 기반 집합은 값들의 단순 리스트로 중복 금지라는 제약이 하나 더 추가된 배열입니다. 이러한 규칙이 하나 추가됨으로써 집합의 효율성이 크게 달라집니다. (효율성이 어떻게 달라지는지는 아래의 집합의 연산에서 이해할 수 있습니다.)
🟪 연산과 연산의 속도
🔶 자료구조의 연산
자료구조의 성능을 알려면 코드가 자료 구조와 어떻게 상호작용하는지 분석해야 합니다. 대부분의 자료구조는 네 가지 기본 방법 : 읽기, 검색, 삽입, 삭제를 사용하며 이를 연산이라 부릅니다.
- 읽기
: 읽기는 자료구조 내 특정 위치를 찾아보는 것이다. 값을 반환한다.- 검색
: 검색은 자료 구조 내에서 특정 값을 찾는 것이다. 인덱스를 반환한다.- 삽입
: 삽입은 자료 구조에 새로운 값을 추가하는 것이다.- 삭제
: 삭제는 자료 구조에서 값을 제거하는 것이다.
🔶 자료구조의 속도 측정
연산이 얼마나 빠른가 측정할 때는 '시간 관점'이 아니고 '얼마나 많은 단계 [ step ] 가 필요한가' 라는 관점이 기준이다.
-
왜 코드의 속도를 단계로 측정할까?
: 정확히 몇초 몇분이 걸린다고 단정할 수 없기 때문입니다. 같은 연산이라도 어떤 컴퓨터에서는 5초가 걸리고, 구형 하드웨어에서는 더 오래 걸릴 수도 있습니다. 미래의 신형 컴퓨터에서는 1초가 걸릴 수도 있습니다.➡️ 시간은 연산을 실행하는 하드웨어에 따라 항상 바뀌므로 시간을 기준으로 속도를 측정하면 신뢰할 수 없다.
- 대신 연산의 속도를 "얼마나 많은 계산 단계
step가 필요한가"로 측정한다면?
: 연산 A가 5단계가 필요하고 연산 B에 500단계가 필요하면, 모든 하드웨어에서 연산 A가 연산 B보다 항상 빠를 거라고 가정할 수 있습니다.
🟪 🌟 배열 연산의 속도 🌟
🔶 읽기 : [ ①단계 ]
배열의 읽기 연산은 한 단계로 끝나는 가장 빠른 연산 유형이다.
❗컴퓨터는 딱 한 단계로 배열에서 읽을 수 있다. 배열 내 특정 인덱스에 한 번에 접근해서 볼 수 있기 때문이다.
↳ 예를 들어 배열의 인덱스 2를 찾아본다면 컴퓨터는 인덱스 2로 바로 가서 어떠한 값이 있다고 알려줄 것이다.
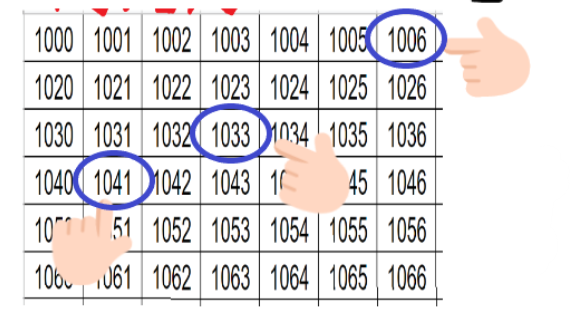
❗컴퓨터의 메모리는 셀로 구성된 거대한 컬렉션이라고 볼 수 있는데, 메모리 내에 각 셀에는 특정 주소가 있다. 각 셀의 메모리 주소는 앞 셀의 주소에서 1씩 증가한다
❗컴퓨터는 모든 메모리 주소에 한 번에 갈 수 있다.
↳ 예를 들어 메모리 주소 1063에 있는 값을 조사하라고 요청하면 검색 과정없이 한 번에 바로 즉시 가서 찾아낸다.
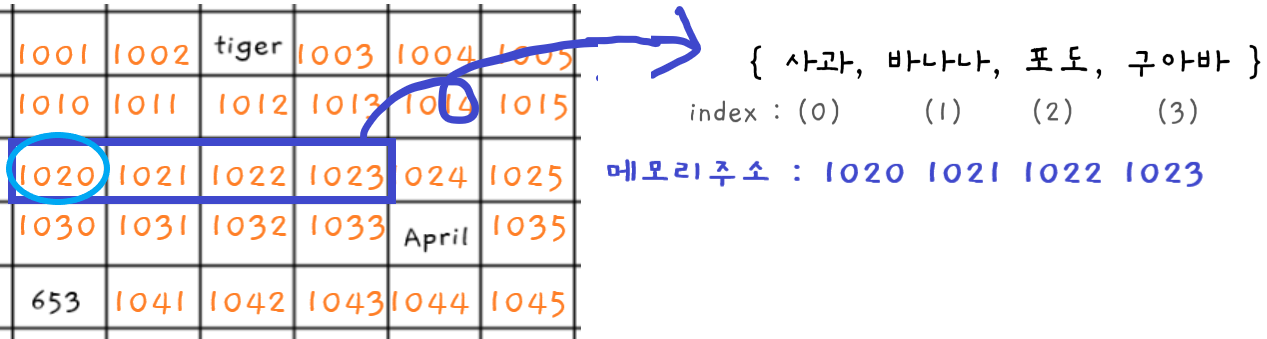
❗프로그램에서 배열을 선언하면 컴퓨터는 프로그램이 쓸 수 있는 연속된 빈 셀들의 집합을 할당한다. 컴퓨터는 배열을 할당할 때 어떤 메모리 주소에서 시작하는지도 기록해둔다.
↳ 예를 들어 원소 4개를 넣을 배열을 생성하면 컴퓨터는 한 줄에서 4개의 빈 셀 그룹을 찾아 사용자가 사용할 배열로 정한다. 그리고 이 배열이 메모리 주소 1020에서 시작하는 것을 기억해둔다.
❗컴퓨터는 배열의 어떤 인덱스에 있는 값이든 간단한 덧셈을 수행해 찾을 수 있다. 배열의 인덱스 3의 값을 읽으라고 명령하면 인덱스 0의 메모리 주소를 가져와 3을 더한다.
↳ 예를 들어 아래의 배열은 메모리 주소 1020에서 시작한다.
배열의 첫 번째 값은 한 번에 1020으로 가서 찾는다.
배열의 세 번째 값은 1020+3을 하여 1023 메모리 주소로 가서 찾는다.
String[] fruits = { "사과", "바나나", "포도", "구아바"}; System.out.println( fruits[2] )↳ fruits 배열을 선언하였을 때, 컴퓨터는 [ 1020 ~ 1023 ] 까지의 4개의 연속된 셀들의 집합을 할당하고, 이 배열이 1020에서 시작함을 기억한다.
fruits[2], fruits배열의 2번 째 인덱스를 읽기 했을 때, 컴퓨터는 메모리의 1020번을 바로 찾아가,+2를 하여 1022번에 있는 값을 읽는다.
단 한 단계만에 컴퓨터는 읽기를 완료하였다.
🔶 검색 : 🌟 선형검색 🌟 : [ ⓝ단계 ]
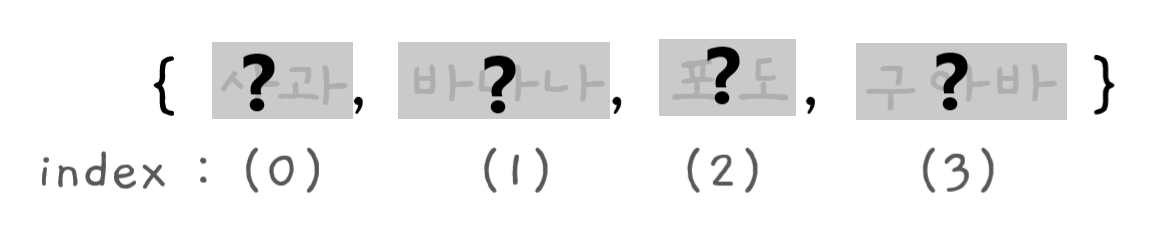
컴퓨터는 각 셀에 실제 어떤 내용이 들어 있는지 바로 알 수 없다.
배열에서 해당 값을 검색해 보려면 하나씩 전부 조사하는 방법 밖에 없다.
❗컴퓨터가 한 번에 한 셀씩 확인하는 방법을 선형검색이라 부른다.
배열에서 "포도"라는 값을 찾아보자.

1단계 : 인덱스 0의 값을 확인한다. fruit[0]은 "사과"이다. 검색값과 일치하지 않으므로 다음 인덱스로 이동해서 검색을 계속한다.
2단계 : 인덱스 1의 값을 확인한다. fruit[1]은 "바나나"이다. 검색값과 일치하지 않으므로 다음 인덱스로 이동해서 검색을 계속한다.
3단계 : 인덱스 2의 값을 확인한다. fruit[2]은 "포도"이다. 검색값과 일치하므로 마친다.
컴퓨터는 찾으려는 값을 발견할 때까지 선형검색을 통해 3단계가 걸렸다.
예를 들어 검색값이 배열의 마지막 인덱스에 위치하고 있다면,
배열의 길이가 5이면 5단계가, 500이면 500단계가 걸린다.
❗배열의 원소가 N개일 때, 배열의 검색은 선형 검색을 하므로, 최대 N단계가 필요하다.
배열의 원소가 몇 개이든 한 단계만 걸리는 읽기 연산보다 검색 연산은 훨씬 비효율적임을 알 수 있다.
🔶 삽입 : [ ⓝ+①단계 ]
배열에 새 데이터를 삽입하는 연산은 배열의 어디에 데이터를 삽입하는 가에 따라 효율성이 다르다.
배열의 맨 끝에는 오직 한 단계만 걸린다. 이것은 컴퓨터는 배열을 할당할 때 항상 배열의 크기와 시작 메모리 주소를 기록한다는 특징에 기인한다.
예를 들어 배열이 메모리 주소 1010에서 시작하고 크기가 5면 마지막 메모리 주소가 1014이다. 따라서 다음 메모리 주소인 1015에 항목을 추가하면 배열의 맨 끝에 삽입이 된 것이다.
배열의 맨 처음에 삽입 시 배열의 원소 개수 만큼의 단계가 걸린다. 이는 삽입할 공간을 만들기 위해 배열 내 모든 값을 한 셀씩 오른쪽으로 옮겨야 하기 때문이다.
🔵 배열의 맨 끝에 삽입할 때 : [ ①단계 ]

❓ 컴퓨터는 애초에 배열에 4개의 메모리 셀을 할당했고 5번째 원소를 추가하려면 이 배열에 셀을 추가로 할당해야 한다. 대부분의 프로그래밍 언어가 내부적으로 자동 처리하지만 언어마다 방식이 다르므로 이 부분은 생략하겠다.
JAVA같은 경우는 배열에 삽입이나 삭제를 할 때 마다 배열을 새로 만든다. 즉, 메모리에 다시 할당을 한다.
🔵 배열의 처음/중간에 삽입 할 때 : [ ⓝ+①단계 ]

"딸기"를 넣을 공간을 만들기 위해서 마지막 셀부터 뒤로 옮긴다.
1단계 : "구아바"를 오른쪽으로 옮긴다.
2단계 : "포도"를 오른쪽으로 옮긴다.
3단계 : "바나나"를 오른쪽으로 옮긴다.
4단계 : "사과"를 오른쪽으로 옮긴다.
4단계 : "딸기"를 넣을 인덱스0이 비었으므로 이제 삽입할 수 있다.
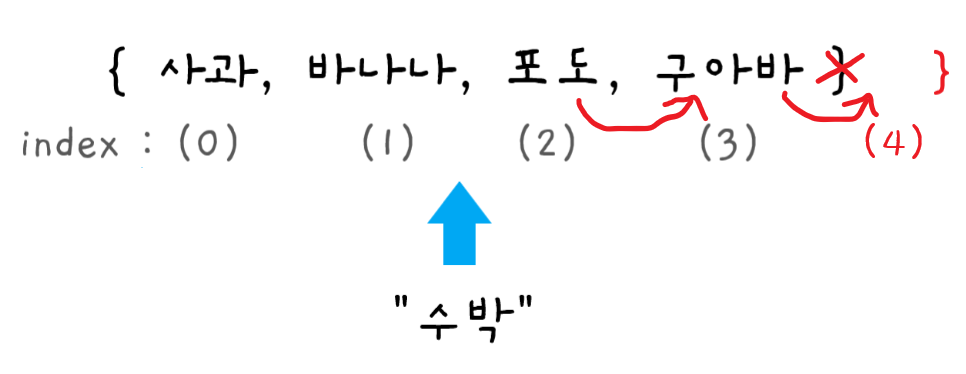
배열의 중간에 삽입할 때도 마찬가지이다. 삽입하고 싶은 인덱스를 비우기 위해서 기존의 데이터들을 뒤로 옮긴다.
1단계 : "구아바"를 오른쪽으로 옮긴다.
2단계 : "포도"를 오른쪽으로 옮긴다.
3단계 : "포도"를 넣을 인덱스1이 비었으므로 삽입한다.
❗원소가 N개인 배열에서 최악의 시나리오인 배열의 맨 앞에 삽입할 때는 N+1단계가 걸린다. N개의 원소를 전부 이동시키고 끝으로 실제 삽입 단계를 실행해야 하기 때문이다.
🔶 삭제 [ ⓝ단계 ]
삽입과 과정이 비슷하다.
배열에서 "사과"라는 값을 삭제 해보자.

1단계 : "사과"를 삭제한다.
1단계 : "바나나"를 왼쪽으로 옮긴다.
2단계 : "포도"를 왼쪽으로 옮긴다.
3단계 : "구아바"를 왼쪽으로 옮긴다.
데이터를 해당 인덱스에서 삭제를 하고 나면, 배열에 빈 공간이 생긴다.
빈 공간의 오른쪽에 있는 데이터들을 왼쪽으로 옮겨 이 문제를 해결한다.
첫 번째 원소를 삭제하는 것이 인덱스 0이 비게 되고, 남아 있는 모든 원소를 왼쪽으로 이동 시켜야 하므로 최악의 시나리오이다.
원소 5개이면, 1단계는 원소 삭제, 나머지 4단계는 남은 4개의 원소 이동이다.
원소가 500개일 때도 마찬가지, 1단계는 원소 삭제, 나머지는 남은 499개의 데이터 이동이다.
따라서 ❗원소가 N개인 배열의 삭제에 필요한 최대 단계 수는 N단계이다. 첫 번째 단계가 삭제이고, 나머지 단계는 빈 공간을 메꾸는 데이터 이동이기 때문이다.
🟪 집합의 연산의 속도
🔶 읽기 : [ ①단계 ]
배열 읽기와 완전히 똑같다. 1단계가 걸린다.
컴퓨터는 특정 인덱스에 들어 있는 값을 한 단계 만에 찾는다. 컴퓨터는 메모리 주소를 쉽게 계산해서 접근할 수 있으므로 집합 내 어떤 인덱스든 갈 수 있다.
🔶 검색 : [ ⓝ단계 ]
배열 검색과 완전히 똑같다. 집합에서 어떤 값을 찾는 데 최대 N단계가 걸린다.
🔶 삭제 : [ ⓝ단계 ]
배열 삭제와 완전히 똑같다. 값을 삭제하고 데이터를 왼쪽으로 옮겨 빈 공간을 메꾸는데 최대 N단계가 걸린다.
🔶 🌟 삽입 🌟 : [ ②ⓝ+①단계 ]
집합의 읽기, 검색, 삭제와 배열의 일기, 검색, 삭제는 동일하지만 "삽입"연산에서는 집합과 배열은 다르다. 결론부터 말하자면 집합의 삽입이 배열의 삽입보다 느리다.
배열의 맨 앞에 "딸기"를 삽입해보자.
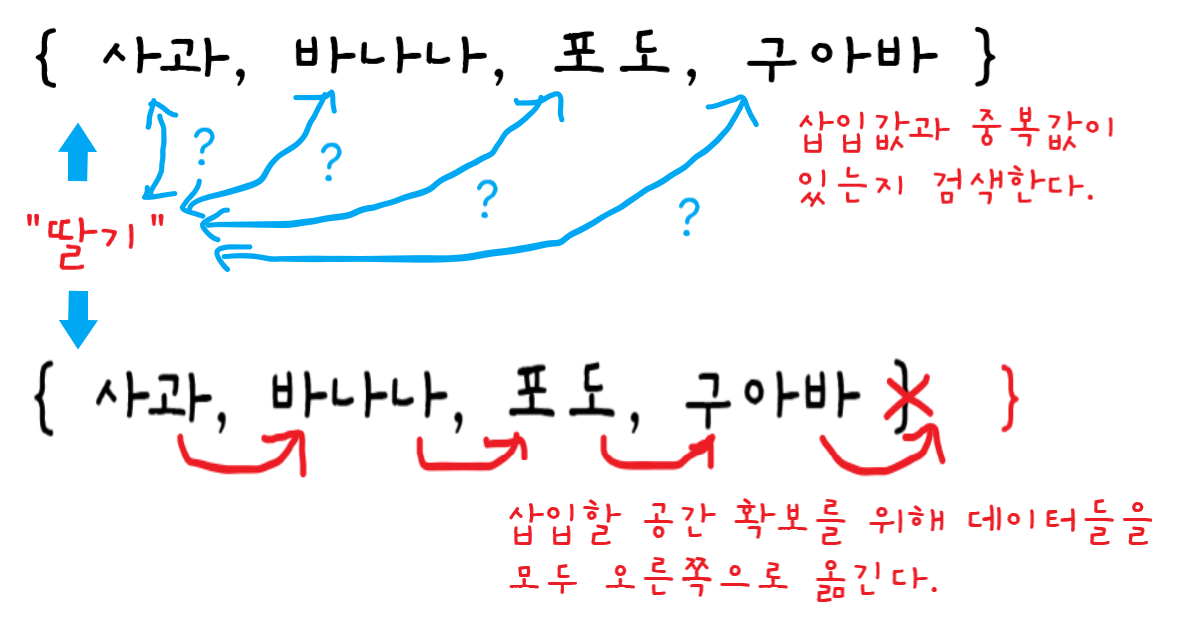
1단계 : 인덱스 0에서 "딸기" 검색한다.
2단계 : 중복값이 없으므로 인덱스 1을 검색한다.
3단계 : 인덱스 2을 검색한다.
4단계 : 인덱스 3을 검색한다.
5단계 : 집합을 전부 검색해도 중복값이 없으므로 "딸기"를 삽입할 수 있다. 0번째 인덱스에 딸기를 삽입하기 위해서는 비어있어야 한다. 0번째 인덱스를 비우기 위해 집합의 모든 데이터들을 오른쪽으로 옮긴다. "구아바"를 오른쪽으로 옮긴다.
6단계 : "포도"를 오른쪽으로 옮긴다.
7단계 : "바나나"를 오른쪽으로 옮긴다.
8단계 : "사과"를 오른쪽으로 옮긴다.
9단계 : 배열의 첫 번째 셀에 "딸기"를 삽입한다.
❗집합에서 삽입할 때는 먼저 이 값이 이미 집합에 들어 있는지 검색해야 하는 것이 우선이다. 중복 데이터를 막는 게 바로 집합의 역할이기 때문이다.
❗집합의 끝에 삽입하면 원소 N개에 대해 최대 N+1단계가 필요하다. N단계의 중복 검색을, 삽입에 1단계를 쓰기 때문이다.
맨 끝에 삽입 시 1단계만 걸리던 배열보다 느리다.
집합의 맨 앞에 삽입하는 것이 최악의 시나리오인데, 이 때 컴퓨터는 N개의 원소를 모두 검색하여 중복 검사를 한 후, 또 다른 N단계로 모든 데이터를 오른쪽으로 옮겨야 하며, 마지막으로 삽입에 1단계가 걸리므로 총 2N+1단계가 필요하다.
맨 앞 삽입 시 N+1단계만 걸리던 배열보다 느리다.
🟦 출처
🔷 글의 내용
이 글 내용은 '제인 웬그로우'의 '누구나 자료구조와 알고리즘 개정 2판' 책을 100% 참고하여 작성하였습니다. 설명에 전문적인 용어보다는 일상적인 용어를 사용하고 그림으로 원리를 설명해주어 왕초보인 저가 이해하기에 아주 좋았습니다. 가격이 많이 나가는 편이지만 꼭 배워야 하는 내용이 모두 들어있고 그것을 제가 이해할 수 있는 수준으로 쓰여있어 전혀 아깝지 않은 소비였습니다.

