🟪 정렬된 배열

ordered array

정렬된 배열과 일반 배열의 차이점은 "값이 항상 순서대로 있어야 한다" 는 점이다.
❗값을 추가할 때마다 적절한 위치에 삽입하여 값을 정렬된 상태로 유지한다.

🔶 삽입 : [ ⓝ+②단계 ]

아래의 정렬된 배열에 75를 삽입해보자.

일반 배열이라면 배열의 맨 끝에 75를 삽입하여 한 단계만 삽입이 처리 된다.

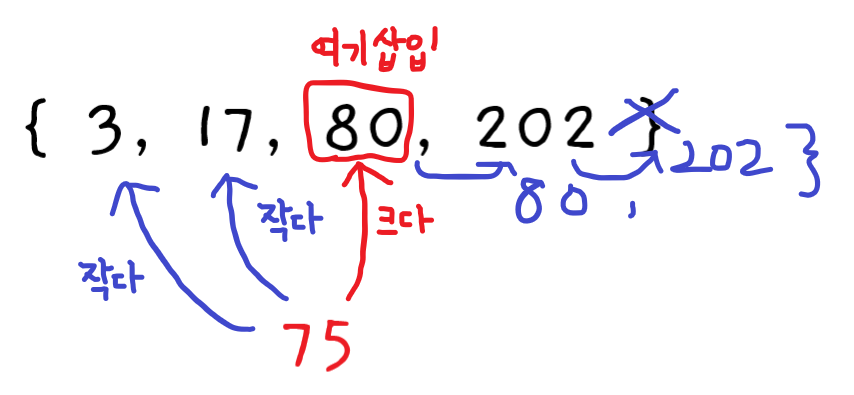
하지만 정렬된 배열에서는 값을 오름차순으로 유지해야 하기 때문에 적절한 위치를 찾고 다른 값들을 옮겨 그 위치를 빈 공간으로 만드는 과정이 추가로 필요하다. 그 다음에 삽입을 처리할 수 있는 것이다.

• 1단계 : [ 비교 ] 인덱스0의 값을 확인하여 삽입값 75와 비교한다. 75는 3보다 크므로 오른쪽에 들어가야 한다. 하지만 정확한 삽입 위치를 알 수 없으므로 다음 셀을 확인해야 한다.

• 2단계 : 인덱스1의 값을 확인한다. 75가 더 크므로 다음 셀을 확인한다.

• 3단계 : 인덱스2의 값을 확인한다. 75보다 더 큰 값이 나왔다! 앞 셀은 75보다 작고 지금 셀은 75보다 큰 첫 값이다. 그러므로 여기 인덱스2에 75를 삽입하면 정렬된 배열을 유지할 수 있다 는 것을 알 수 있다.

• 4단계 : [ 옮기기 ] 인덱스2를 빈 공간으로 만들기 위해 마지막 값인 인덱스3의 값을 오른쪽으로 옮긴다.

• 5단계 : 인덱스3을 오른쪽으로 옮긴다.

• 6단계 : [ 삽입 ] 인덱스2가 적절한 위치이고 빈공간이 되었다. 여기에 75를 삽입한다.

여기서 원소가 4개 였고 비교에 3단계 옮기기에 2단계 삽입에 1단계, 총 6단계가 걸렸다.

그래서 ❗N개의 원소를 가진 정렬된 배열에서 삽입의 연산은 N+2단계가 걸린다고 볼 수 있다.

삽입의 위치가 어디든 단계 수는 비슷하다. 배열 앞 부분일수록 비교가 줄어들지만 이동이 늘어나고, 뒷 부분일수록 비교가 늘어나도 이동이 줄어들기 때문이다.

배열의 맨 끝에 놓이면 이동이 필요없으므로 제일 빠른 경우이다. 이 때는 비교에 N단계와 삽입에 1단계, 총 N+1단계가 걸린다.

가장 느릴 때 N+2단계, 가장 빠를 때 1단계가 걸리는 일반 배열의 삽입에 비해 정렬된 배열의 삽입이 느림을 알 수 있다.

🔶 검색_선형검색 : [ ⓝ단계 ]

"선형검색"으로 정렬된 배열을 검색연산 해보자.
아래의 정렬된 배열에서 존재하지 않는 값 22를 검색해본다면?

정렬된 배열에서는 22보다 큰 값이 나오면 바로 검색을 중단하고 해당 값이 없다고 판단할 수 있다.

선형검색은 정렬된 배열에서 보통은 일반 배열보다 단계 수가 더 적게 걸린다.
하지만 만약 찾으려는 값이 배열에서 제일 큰 값이라면 정렬된 배열과 일반 배열 모두 모든 셀을 검색해야 한다.

그러므로 선형검색으로 정렬된 배열을 검색 연산 한다면 일반배열과 똑같이 ❗N단계가 걸린다.

❕코드 구현 ❗

• 메서드는 두 인수를 받는다.
  • orderedArray : 검색할 정렬된 배열
  • searchValue : 찾으려는 값

• 배열의 모든 원소를 순회한다.

• 원하는 값을 찾으면 그 인덱스를 반환한다.

• 찾고 있던 값보다 큰 원소에 도달하면 루프를 종료한다.

• 배열에서 값을 찾지 못하면 null을 반환한다.

public static Integer linearSearch(int[] orderedArray, int searchValue) {
    for (int index = 0; index < orderedArray.length; index++) {
        if (orderedArray[index] == searchValue)
            return index;

        else if (orderedArray[index] > searchValue)
            break;
    }

    return null;
}

• JUNIT TEST 통과!

import org.junit.Test;
import static org.junit.Assert.*;

@Test
public void linearSearchTest() {
    int[] array1 = {1, 3, 9, 10};

    Integer expectedNull = null;
    Integer expected0 = 0;
    Integer expected1 = 1;
    Integer expected2 = 2;
    Integer expected3 = 3;

    // 예상값 , 실제값
    assertEquals(expectedNull,linearSearch(array1,11));
    assertEquals(expectedNull,linearSearch(array1,2));
    assertEquals(expectedNull,linearSearch(array1,8));

    assertEquals(expected0,linearSearch(array1,1));
    assertEquals(expected1,linearSearch(array1,3));
    assertEquals(expected2,linearSearch(array1,9));
    assertEquals(expected3,linearSearch(array1,10));
}

🔶 검색_🌟이진검색🌟 : [ ⓛⓞⓖⓃ단계 ]

원소가 9개인 정렬된 배열이 있다. 이 배열에 어떤 값들이 있는지 전혀 모르는 상태에서 값 7을 찾아보자.

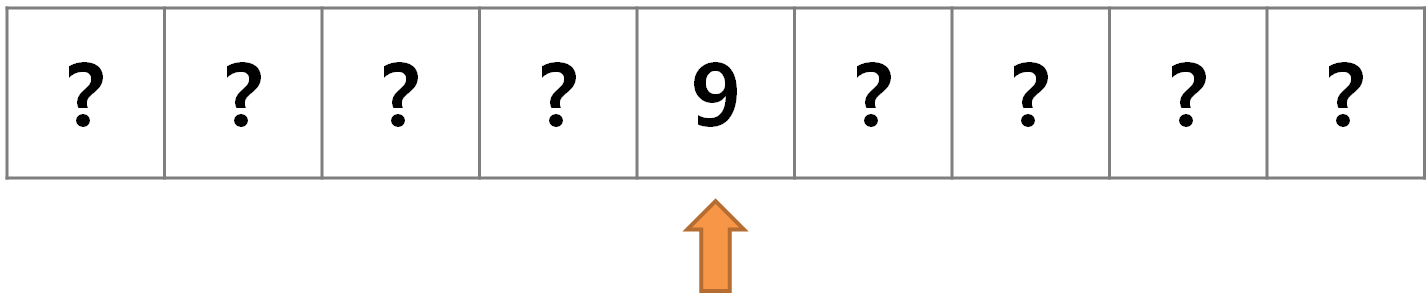
• 1단계 : 가운데 셀부터 검색을 시작한다. 배열의 길이를 2로 나누어 가운데 셀의 인덱스를 계산한다.

가운데 셀의 값은 9이므로 7은 왼쪽 어딘가에 있다. 9와 9보다 오른쪽의 있는 셀 모두가 제거 되었으므로 이로써 배열의 절반이 제거됐다.

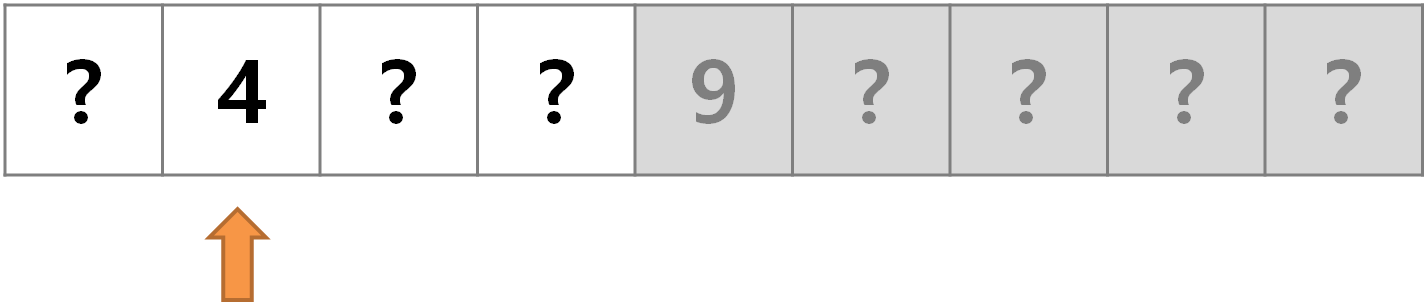
• 2단계 : 9의 왼쪽 셀들 중 가운데 값을 확인한다. 가운데 값이 두 개이므로 임의로 왼쪽 값을 선택한다. 셀의 값이 4이므로 7은 오른쪽 어딘가에 있다. 4와 4의 왼쪽 셀 모두가 제거 되었다.

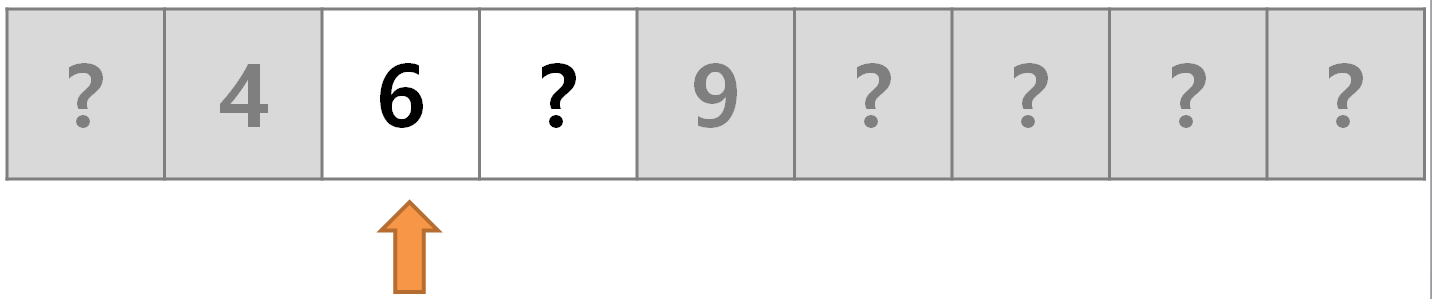
• 3단계 : 7일 수 있는 두 개의 셀 중 임의로 왼쪽 셀을 선택한다. 값이 6이므로 7은 바로 오른쪽에 있다. 만약 거기도 없다면 이 배열에는 7은 없는 것이다.

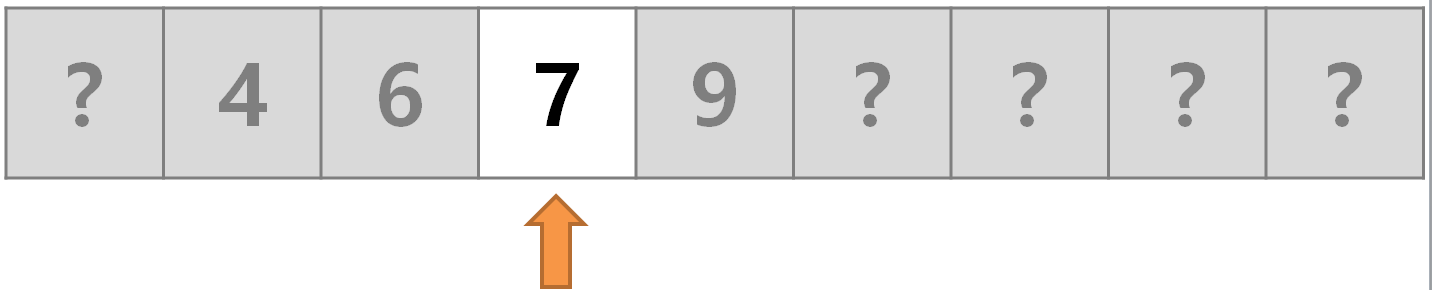
• 4단계 : 4단계만에 검색이 완료됐다.

이진 검색은 정렬된 배열에만 쓸 수 있다.
이진 검색을 쓸 수 있다는 것이 정렬된 배열의 장점 중 하나이다.

검색 값이 배열의 원소 중 가장 큰 값이면 이진 검색에 최대 단계수가 걸린다.
배열의 크기가 3일 때 이진 검색에 필요한 최대 단계 수는 2다.
배열의 크기를 두 배로 늘리면 크기가 7이 되고, 이진 검색에 필요한 최대 단계 수는 3이 된다.
배열의 크기를 두 배로 늘리면 크기가 15가 되고 이진 검색에 필요한 최대 단계 수는 4가 된다.

❗이진 검색을 쓰면 추측할 때마다 검색해야 할 셀 중 절반을 제거할 수 있다. 그러므로 데이터를 두 배로 늘릴 때마다 이진 검색 알고리즘에서는 최대 한 단계만 더 추가된다. 이것을 logN단계가 걸린다고 한다.

❕코드 구현 ❗

• 먼저 찾으려는 값이 있을 수 있는 상한선과 하한선을 정한다.

• 최초의 상한선은 배열의 첫 번째 값, 하한선은 마지막 값이다.

• 상한선과 하한선 사이의 가운데 값을 계속해서 확인하는 루프를 시작한다.

• 루프를 상한선과 하한선이 같아질 때까지만 실행한다.
  • 상한선과 하한선이 같아지면 검색값이 이 배열에 없다는 뜻이므로,

⬇️ 루프안에서

• 상한선과 하한선 사이에 중간 지점을 찾는다.
  • 결괏값이 정수가 아닐 때는 올림한다.
    ↳ java의 ceil함수

• 중간 지점의 값을 확인한다.

• 중간 지점의 값이 찾고 있던 값이면 검색을 끝낸다.

• 아니라면 검색값이 중간지점값보다 작은지, 큰지 확인하여 상한선이나 하한선을 바꾼다.

• 루프를 빠져나오면 배열에 값이 없다는 뜻이므로 null을 반환한다.

public static Integer binarySearch(int[] orderedArray, int searchValue) {
    int lowerBound = 0;
    int upperBound = orderedArray.length - 1;

    while (lowerBound <= upperBound) {
        int midpoint = (int) Math.ceil( ((double) upperBound + lowerBound) / 2 );

        if (searchValue == orderedArray[midpoint])
            return midpoint;
        else if (searchValue < orderedArray[midpoint])
            upperBound = midpoint - 1;
        else if (searchValue > orderedArray[midpoint])
            lowerBound = midpoint + 1;
    }

    return null;
}

• JUNIT TEST 통과!

import org.junit.Test;
import static org.junit.Assert.*;

@Test
public void binarySearchTest() {
    int[] array = {3, 10, 37, 39, 44, 81, 659};

    Integer expectedNull = null;
    Integer expected0 = 0;
    Integer expected1 = 1;
    Integer expected2 = 2;
    Integer expected3 = 3;
    Integer expected4 = 4;
    Integer expected5 = 5;
    Integer expected6 = 6;

    //예상값, 실제값
    assertEquals(expectedNull, binarySearch(array, 788));
    assertEquals(expectedNull, binarySearch(array, 45));
    assertEquals(expectedNull, binarySearch(array, 2));
    assertEquals(expected0, binarySearch(array, 3));
    assertEquals(expected1, binarySearch(array, 10));
    assertEquals(expected2, binarySearch(array, 37));
    assertEquals(expected3, binarySearch(array, 39));
    assertEquals(expected4, binarySearch(array, 44));
    assertEquals(expected5, binarySearch(array, 81));
    assertEquals(expected6, binarySearch(array, 659));
}

🟪 선형검색 vs 이진검색

작은 크기의 배열이라면 이진 검색 알고리즘이 선형 검색 알고리즘보다 크게 나은 점은 없다. 하지만 배열이 더 커질 수록 이진 검색이 훨씬 선형 검색보다 빨라진다.

100개의 원소를 가진 배열에서 검색 연산에 필요한 최대 단계수 :

• 선형 검색 : 100단계
• 이진 검색 : 7단계

원소가 10,000개일 때 :

• 선형 검색 : 10,000단계
• 이진 검색 : 13단계

원소가 1,000,000개 일 때 :

• 선형 검색 : 1,000,000단계
• 이진 검색 : 20단계

선형 검색에서는 원소 수만큼의 단계가 필요하다. 배열의 원소 수를 두 배로 늘릴 때마다 단계 수도 두 배로 늘어난다. 반면 이진 검색에서는 한 단계만 늘어난다.

⬇️ 선형 검색과 이진 검색의 이러한 성능 차이를 그래프로 표현하면

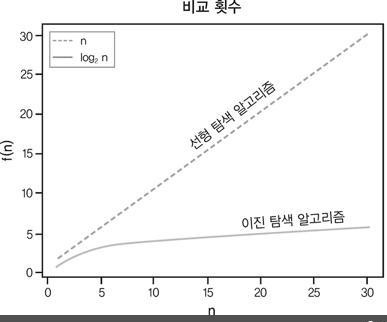
선형 검색에 해당하는 선을 보면 배열에 원소가 많아질수록 그에 비례해 검색에 걸리는 단계 수도 늘어난다. 기본적으로 배열에 원소 하나가 늘어날 때마다 선형 검색에는 4단계가 더 걸린다. 그래서 대각선 형태의 직선이 만들어진다.

이진 검색에 해당하는 선을 보면 데이터가 많아질수록 알고리즘의 단계 수는 아주 조금만 늘어난다. 이진 검색이 한 단계 늘어나려면 데이터 크기를 두 배로 늘려야 한다는 사실에 완벽히 부합한다.

🟪 알고리즘이란

알고리즘은 특정 과제를 달성하기 위해 컴퓨터에 제공되는 명령어 집합이다.
어떤 코드를 작성하든 컴퓨터가 따르고 실행할 알고리즘을 만드는 것이다.

• 예시

public static void printThings() {
    String[] things = {"apples", "chairs", "files", "notes"};

    for (String thing : things)
        System.out.printf("Here's a thing : %s \n", thing);
}

복잡하지 않을지라도 뭔가를 하는 코드는 모두 엄밀히 알고리즘, 즉 문제를 풀어나가는 절차다. 이 코드는 리스트의 모든 항목을 출력하고 싶다는 문제를 해결한다. 이 문제를 푸는 데 사용한 알고리즘은 print문이 포함된 for 루프다.

🟪 알고리즘이 중요한 이유

선형 검색과 이진 검색의 성능 차이처럼, 같은 자료구조와 같은 연산을 하더라도 선택한 알고리즘에 의해서 속도 차이가 확연하게 날 수 있기 때문이다.

---

🟦 출처

🔷 그림1

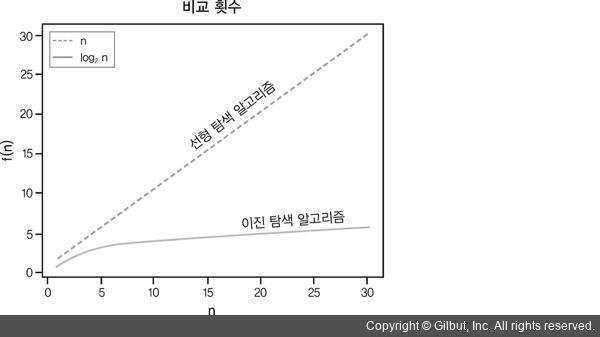
🖱 클릭! | '더 북'사이트의 '컴퓨터 사이언스 부트캠프 with 파이썬' 게시글의 '그림 15-4 선형 탐색 알고리즘 vs. 이진 탐색 알고리즘'표 보러가기

🔷 글의 내용

이 글 내용은 '제인 웬그로우'의 '누구나 자료구조와 알고리즘 개정 2판' 책을 100% 참고하여 작성하였습니다. 설명에 전문적인 용어보다는 일상적인 용어를 사용하고 그림으로 원리를 설명해주어 왕초보인 저가 이해하기에 아주 좋았습니다. 가격이 많이 나가는 편이지만 꼭 배워야 하는 내용이 모두 들어있고 그것을 제가 이해할 수 있는 수준으로 쓰여있어 전혀 아깝지 않은 소비였습니다.

🖱 클릭! | '제인 웬그로우'의 '누구나 자료구조와 알고리즘' 책 구경하러 가보기