레드블랙 트리 구현 ( 삭제 )
오늘은 레드-블랙 트리의 삭제 연산에 대해서 공부를 해봤는데요
자, 한번 시작해볼까요
우리 지난 시간에 레드-블랙 트리의 개념을 공부했죠?
레드-블랙 트리의 조건
- 모든 노드는 red or black
- 트리의 루트 노드는 black, 모든 nil 노드는 black
- 노드의 색이 red 이면 그 노드의 자식은 black
- 어떤 노드에서 nil 까지 black노드의 수는 same = same
개념을 안 보고 오셨다구요? 그럼 아래 링크에 제가 다 정리를 해놨죠-
[개념] 레드-블랙 트리
위에 링크를 가지 않은 사람들이 있다는 것을 저는 알고있답니다.
그래서 제가 삭제 연산의 케이스들을 가져와봤어요-
아래의 케이스들은 삭제 후, 트리들을 재조정하기 위해 사용되는 조건들ez요
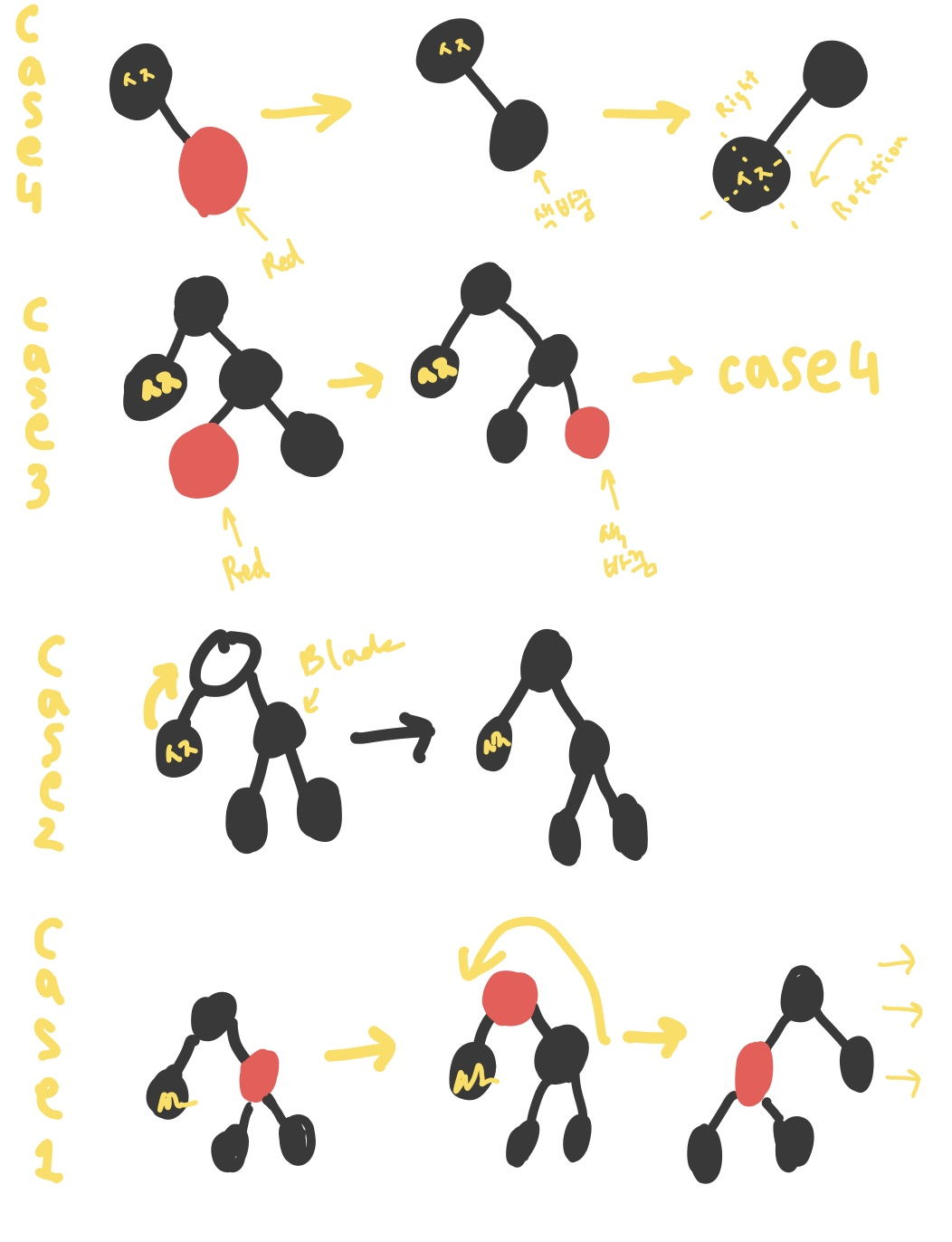
삭제 연산 4 cases
case 4. doubly black 의 형제가 black, 그 형제의 오른 자식이 red일 경우
오른 자식의 색을 바꾸고 doubly black의 부모를 기준으로 left rotation
더블리가 루트가 되면 loop 종료-
case 3. doubly black 의 오른쪽 형제가 black, 그 형제가 왼 자식이 red일때
오른 자식이 블랙일때→
doubly black 의 형제의 오른 자식이 red가 되게 만들어야함
왼 자식과 바꾸고 오른쪽으로 회전하고 case 4의 해결방식을 적용-
case 2. doubly black 형제가 black, 자식도 모두 black일때
부모에게 extra black위임
case 1. doubley black의 형제가 red, 형제와 부모의 색을 바꾸고,
부모 노드를 기준으로 왼쪽으로 회전→ 앞의 case들 중 하나로 해결-↓ 아래와 같이 그림으로 표현할 수 있습니다 ↓
코드를 구현하면서 가장 힘들었던 부분
책에서 더블리 블랙이라는 개념이 나왔었는데 그 개념을 코드에 입히는 과정이 조금 어려웠다
블로그 코드 자료들을 찾아 보니 따로 더블리 블랙이라는 걸 지정해주지 않고 삭제 할 색을 저장해두는 형식으로 연산을 진행하는 방식으로 해결했습니다
혹싀 저의 레드-블랙 트리의 전체 소스 코드가 보고 싶으시다면?
친절한 제가 링크를 달아놨답니다~

