문제 풀러 가기

최대공약수와 최소공배수 (Lv.1)

---

문제

두 수를 입력받아 두 수의 최대공약수와 최소공배수를 반환하는 함수, solution을 완성해 보세요. 배열의 맨 앞에 최대공약수, 그다음 최소공배수를 넣어 반환하면 됩니다. 예를 들어 두 수 3, 12의 최대공약수는 3, 최소공배수는 12이므로 solution(3, 12)는 [3, 12]를 반환해야 합니다.

제한 사항

• 두 수는 1이상 1000000이하의 자연수입니다.

입출력 예

n	m	return
3	12	[3,12]
2	5	[1,10]

입출력 예 설명

입출력 예 #1
위의 설명과 같습니다.

입출력 예 #2
자연수 2와 5의 최대공약수는 1, 최소공배수는 10이므로 [1, 10]을 리턴해야 합니다.

---

접근

최대공약수(Gratest Common Divisor; GCD)

두 수, 혹은 그 이상의 여러 수의 공통인 약수를 뜻함

최소공배수(Least Common Multiple; LCM)

두 수, 혹은 그 이상의 수들의 공통인 배수를 말한다

유클리드 호제법

최대공약수, 최소공배수를 구할 수 있는 공식을 찾으면 비교적 코드로 응용하기 좋은 유클리드 호제법이 나온다.
출처

최대공약수 구하기

다시 말해 두 개의 상수 a가 b보다 크다는 가정하에 a를 b로 나눈 나머지 값 r이 0이면 b가 최대공약수가 된다고 한다.
만약 0으로 나누어지지 않는다면 작은 상수 b와 r을 (r = 0)이 될때까지 계속해서 나누면 마지막 상수 b가 최대공약수다.

입력값 1	입력값 2	나머지
72	60	12
60	12	0

72와 60의 최대공약수는 12

입력값 1	입력값 2	나머지
72	30	12
30	12	6
12	6	0

72와 60의 최대공약수는 6

따라서 나머지가 0이 나올때까지 입력값과 나머지를 계속해서 나누는 반복문 또는 재귀함수를 사용해야 한다는 결론 도출

최소공배수 구하기

원리까지 이해하기엔 수학적 지식이 모자라기에 최소공배수를 구하기 위한 아래 공식만을 응용하기로 했다.

최소공배수(LCM) = (입력값 A * 입력값 B) / 최대공약수(GCD)

참조

int Gcd(int a, int b) {
	int r = a % b;
	if (r == 0)
		return b;
	else
		return Gcd(b, r);
}

---

풀이

풀이 (1): while Loop

// 반복문
function solution(int1, int2) {
    // 최초 입력값의 곱을 미리 할당
    const GCD = int1 * int2;
    // 나머지r값이 0이 될때까지 remainder 수행
    while (int2 !== 0) {
        const r = int1 % int2;
        int1 = int2;
        int2 = r;
    };
    // [최대공약수, 최소공배수] 반환
    return [int1, GCD / int1];
}

0에 수렴할때까지 계속해서 공식을 수행하는 while을 사용했다.
r에는 나머지 값을, 작은 상수에는 r 값을 재할당해서 반복 연산

풀이 (2): Recursion (미완성)

// 재귀문
const solution3 = function(a, b) {
  const GCD = a * b;
  // 쵀대공약수 구하기
  const findLCM = (a, b) => {
    let r = a % b;
    return r === 0 ? b : findLCM(b, r);
  };
  const LCM = findLCM(a, b)
  // 최소공배수 구하기
  return [LCM, GCD / LCM];
};

console.log(solution3(72, 60));
// Expected output: [12, 360]
console.log(solution3(2, 5));
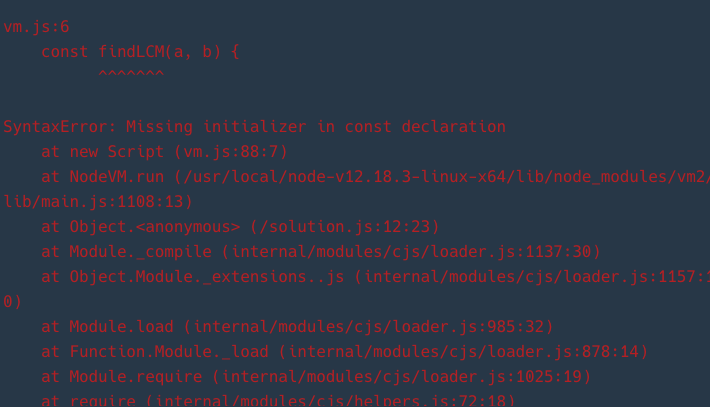
// Expected output: [1, 10]

vs 코드에선 결과값이 잘 나오는데, 프로그래머스 콘솔에선 계속해서 오류가 나온다. 내가 잘못한거겠지

---

다른 사람의 풀이

다른 풀이 (1)

function greatestCommonDivisor(a, b) {return b ? greatestCommonDivisor(b, a % b) : Math.abs(a);}
function leastCommonMultipleOfTwo(a, b) {return (a * b) / greatestCommonDivisor(a, b);}
function gcdlcm(a, b) {
    return [greatestCommonDivisor(a, b),leastCommonMultipleOfTwo(a, b)];
}

console.log(gcdlcm(3,12));

함수명이 너무 길어서 가독성이 떨어지긴 하지만 간단해보이는 방법

• 첫번째 함수는 삼항 연산자와 재귀 함수를 사용하여 최대공약수를 구하는 함수. Math.abs의 용도는 잘 모르겠다
• 두번째 함수는 두 개의 수를 곱한 후 최대공약수로 나누어 최소공배수를 구하는 함수
• 세번째 함수는 위 두 함수를 순차적으로 실행하여 배열안에 담아 반환하기 위한 함수

다른 풀이 (2)

function gcdlcm(a, b) {
    var r;
    for(var ab= a*b;r = a % b;a = b, b = r){}
    return [b, ab/b];
}

생각 없이 썼던 for문의 조건식을 제대로 응용한 방법
for (초기화식; 조건식; 증감식)
두번째 조건식 r = a % b가 0(falsy)이 될때까지 다시 a에 b를, b에 r을 할당하여 반복하는 방법이 참 간단하고 멋지다