제 1장) 추상화에서 보편만능기계까지(2)

5. 정지문제

• 모든 문제는 정지 문제로 귀결된다.

  정지 문제

  • 준비물
    1) A 머신 : 숫자를 입력받아 합을 출력해주는 기계로 숫자가 아닌 다른 것이 들어오면 멈춤
    2) C 머신 : 체스판 그림을 입력받아 말을 어떻게 놓아야 할 지를 알려주는 그림을 출력해주는 기계로 체스판이 아닌 다른 것이 들어오면 멈춤
    3) H 머신 : 머신과 값을 입력받아 머신이 입력값에 대해 멈출지, 멈추지 않을 지 판단할 수 있는 기계
    4) N 머신 : 입력값이 ‘멈춤’이라면 ‘멈추지 않음’을 출력하고, 입력값이 ‘멈추지 않음’이라면 ‘멈춤’을 출력하는 기계
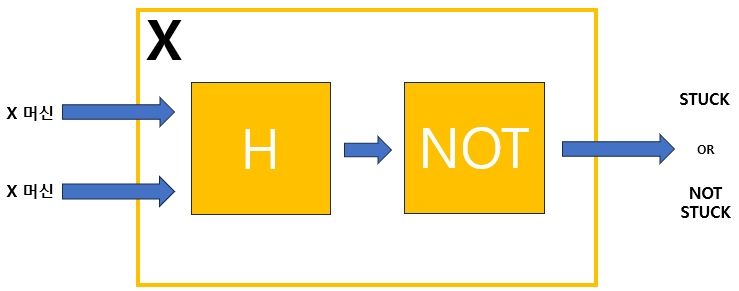
    5) X 머신 : H 머신과 N 머신을 순서대로 결합한 기계
  • Question
    : H 머신이 모든 것을 true, false로 판단할 수 있는 기계라면 컴퓨터는 모든 문제를 해결할 수 있는가?
  • Answer
    : 답은 ‘no’이다.
    만약, H 머신에다가 A 머신과 3+5를 입력해보자. H 머신의 출력값은 ‘멈추지 않음’일 것이다.
    이번엔 H 머신에다가 C 머신과 체스판 그림을 입력해보자.
    이번에도 H 머신은 ‘멈추지 않음’을 출력할 것이다.
    그렇다면 반대로 A 머신과 체스판 그림을, C 머신과 3+5를 넣어보자.
    이번에는 두 경우 모두 ‘멈춤’을 출력할 것이다.
  • 드디어 X 머신이다.
    1) X 머신에다가 X 머신과 X 머신을 넣어보자.
    X 머신 안에 있는 H 머신이 X 머신과 X 머신을 입력받아 출력값으로 ‘멈춤’을 출력하면 X 머신은 N 머신 때문에 ‘멈추지 않음’을 출력할 것이다.
    2) 반대로 H 머신이 X 머신과 X 머신을 입력받아 출력값으로 ‘멈추지 않음’을 출력하면 X 머신은 N 머신 때문에 ‘멈춤’을 출력할 것이다.
    3) X 머신에다가 X 머신과 X 머신을 입력했을 때 H머신은 ‘멈춤’이 나온다고 했지만 실제로 X 머신에다가 X 머신과 X 머신을 입력한 결과 ‘멈추지 않음’이 나오는 것을 볼 수 있다.
    → 이를 통해, 컴퓨터는 모든 문제를 해결할 수는 없다는 결론에 도달하게 된다.
    

6. 튜링머신

• 영국의 수학자 앨런 튜링이 만들어 낸 기계이다. 오늘날 컴퓨터 이론의 시초라고 볼 수 있다.
  정지문제를 통하여 힐베르트의 주장이 틀렸다는 것을 증명하기 위해 발명하였다.

  힐베르트의 주장

  1. 수학은 완전하다
  2. 수학은 일관적이다
  3. 수학은 결정가능하다.

  수학자 괴델은 힐베르트의 주장이 모두 틀렸다는 것을 증명해냈고, 튜링은 이에 더하여 ‘수학은 결정가능하다’는 주장이 틀렸다는 것을 다시 한 번 [정지문제의 모순]을 통하여 증명해냈다.

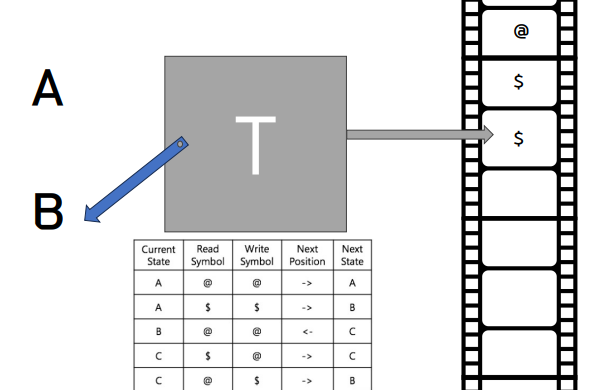
• 위 사진은 튜링머신을 아주 간략하게 나타낸 것이다.

  1. 현재의 값을 읽는다.
  2. 읽은 그 자리의 값에 지시하는 값을 덮어쓴다.
  3. 지시하는 방향대로 움직인다.
  4. 지시하는 다음 상태로 변환한다.

7. 컴퓨터 구조

• 튜링은 힐베르트의 결정가능이론이 틀렸다는 것을 증명하기 위해 정지문제를 고안해 냈으며 이를 통해 튜링머신을 만들어 냈다. 정지문제와 튜링머신의 그림을 보면 매우 유사하다는 것을 알 수 있다.
  컴퓨터 구조는 매우 간단히 <메모리, 프로그램, 판단장치, 입출력장치>로 구분할 수 있는데, 튜링머신에서 그 역할들을 찾아볼 수 있다.
  • 튜링머신

    메모리 - 필림
    프로그램 - 지시 표
    판단 - T 머신
    입출력장치 - 스캐너

• 따라서 우리는 현재의 컴퓨터 구조가 튜링의 컴퓨터 구조와 크게 다르지 않다는 것을 알 수 있으며, 현재의 컴퓨터 이론이 튜링 머신의 구조로부터 시작되었다는 것을 알 수 있다.

< 제 1장을 마치며>

• 컴퓨터 공부를 시작하기 전 영화 이미테이션 게임을 2번 봤었다. 무슨 내용인지는 잘 모르겠는데 그냥 재밌어서 봤었던 것 같다.
  수업 내용을 정리하며 한 번 더 보게 되었는데 그래도 관련 내용을 좀 더 배웠다고, 혹시 아는 내용이 나올 수도 있지 않을까, 왠지 모르게 더 기대감을 가지고 흐뭇하게 영화를 볼 수 있었다.
  참 신기하다. 수학은 완전하지 않다는 것을 증명하기 위해 만든 이론을 통해 거의 완벽에 가까운 기계를 만들어냈기 때문이다.
  겨우겨우 첫 내용을 정리해 봤는데 처음 해보는 정리라 이렇게 하는 게 맞는 건지는 잘 모르겠지만 일단 강의를 들으면서 생각나는 것들을 최대한 깔끔하게 정리해보았다.
  이만 첫 포스팅을 마치겠다.
  안녕~