[EECS 498-007 / 598-005] 강의정리 - 20강 Generative Models II
[CS231n] + [EECS 498-007 / 598-005]

Generative Models II
- Variational Autoencoders
1.1) VAE : Train
1.2) VAE : Generating Data
1.3) VAE : Editing with z\bold zz
1.4) VAE : Summary
1.5) Autoregressive models vs Variational models - Vector-Quantized Variational Autoencoder (VQ-VAE2)
- Autoregressive model, VAE, GANs Overview
- Generative Adversarial Networks
4.1) GANs : Training Objective
4.2) GANs : Optimality
4.3) GANs : DC-GAN
4.4) GANs : Vector Math
4.5) GAN Improvments - Conditional GANs
5.1) Conditional Batch Normalization
5.2) Spectral Normalization
5.3) Self-Attention
5.4) BigGAN
5.5) Generating Videos with GANs
5.6) Conditioning on more than labels! Text to Image
5.7) Image Super-Resolution: Low-Res to High-Res
5.8) Image-to-Image Translation: Pix2Pix
5.9) Unpaired Image-to-Image Translation: CycleGAN
5.10) Label Map to Image
5.11) GANs: Not just for images! Trajectory Prediction - Generative Models Summary
1. Variational Autoencoders
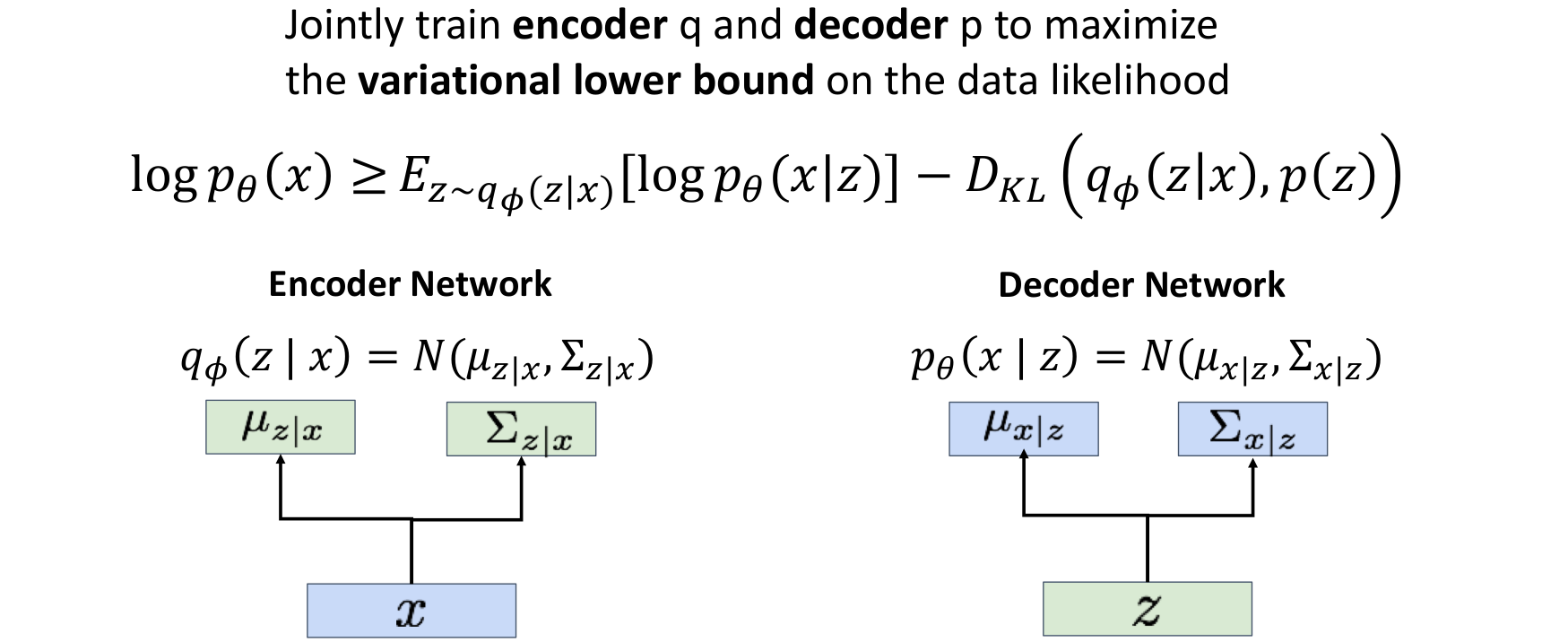
✅️ Example : Fully-Connected VAE
MNIST Dataset
:28 x 28image, flattened to784-dim vector
:20-dim vector (hyper-parameter)
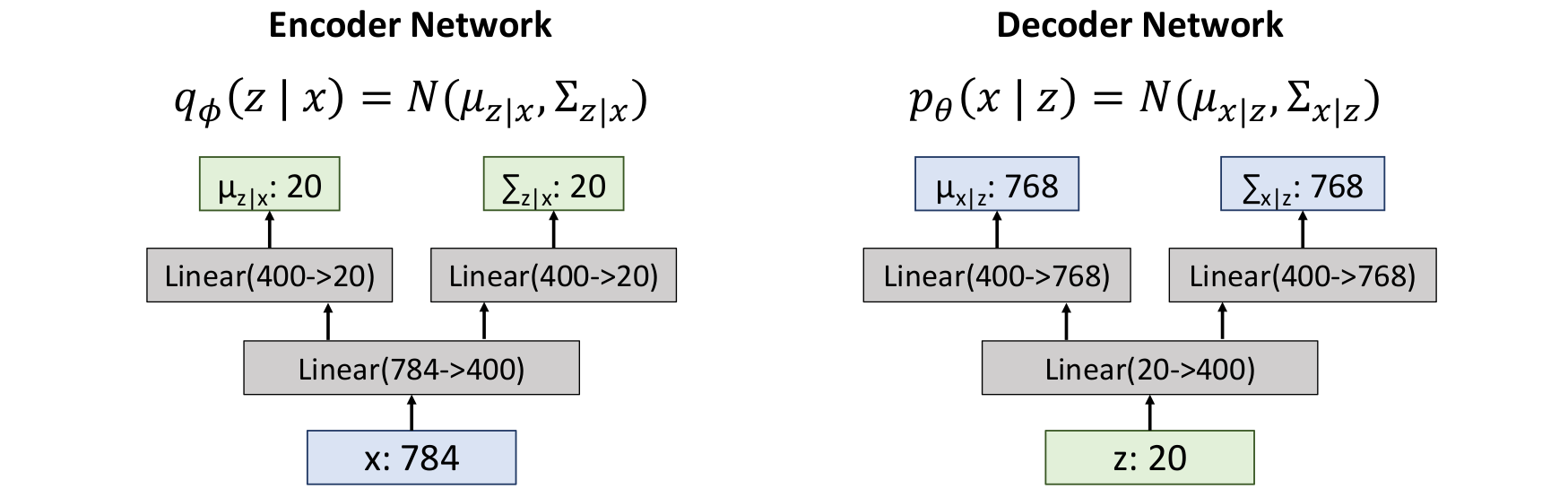
Decoder에서 output은 768이 아니라 784임.
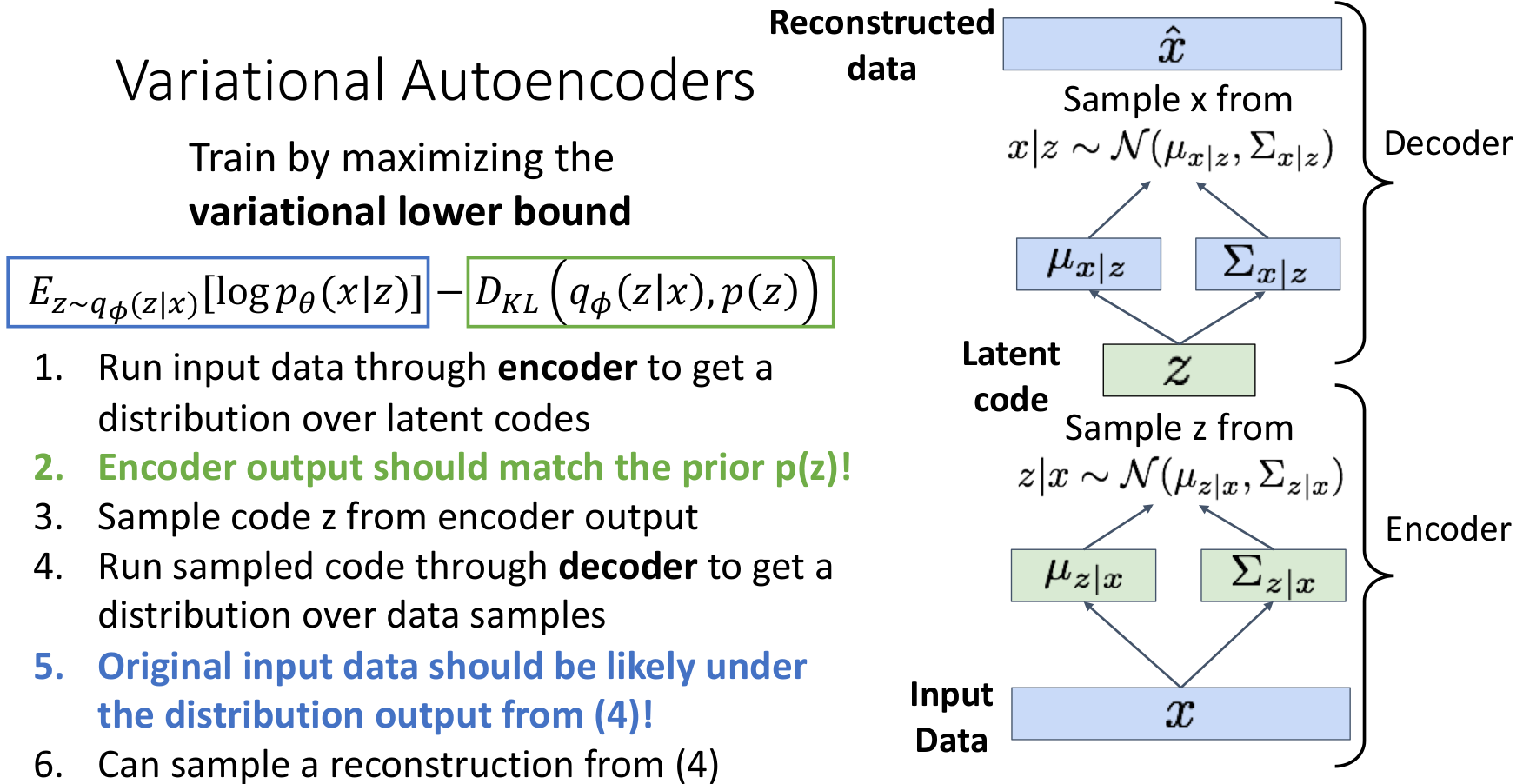
1.1) VAE : Train
그렇다면 어떻게 이 모델을 학습시킬까?
Maximize Variational lower bound
-
input data 를
encoder에 넣어서x에 대한z의 distribution을 얻는다.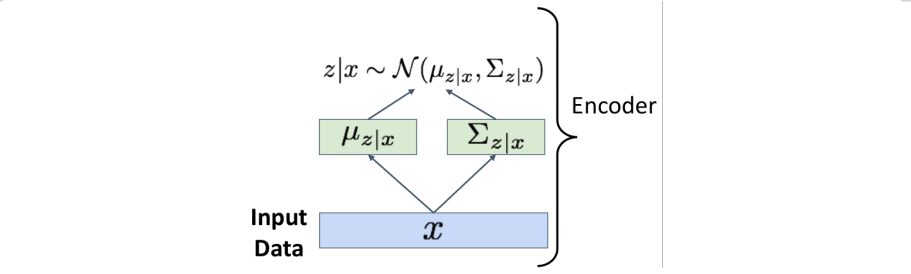
-
Encoderoutput should match the prior !
2번에서는를 계산할 수 있다.
encoder의 output은 이고, 우리가 학습하기 전 unit gaussian으로 정해놓은 의 prior distribution이 이다.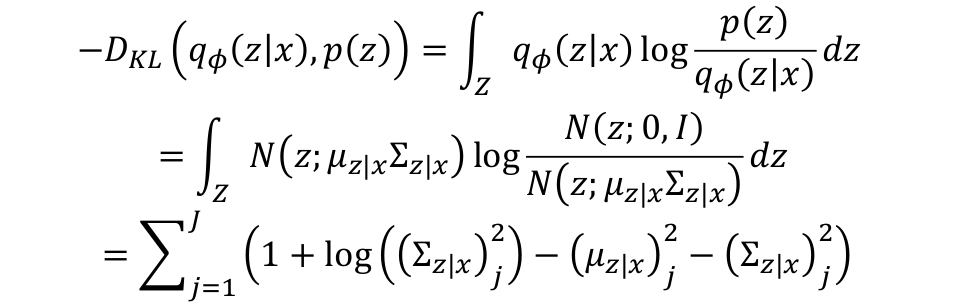 모든 distribution을 Gaussian으로 설정했기 때문에 가 diagonal Gaussian이고, 가 unit Gaussian일 때, closed form solution을 구할 수 있다.
모든 distribution을 Gaussian으로 설정했기 때문에 가 diagonal Gaussian이고, 가 unit Gaussian일 때, closed form solution을 구할 수 있다. -
앞서 구한 distribution
들로 부터, 각각 를 sampling하여 Latent code 를 구한다.
-
Decoder에z를 통과시켜 data samples 에 대한 distributions를 구한다. -
Original input data 는 4번의 output distribution에 존재해야한다.(존재할 가능성이 높아야 한다.) Original input data should be likely under the distribution output from (4)!
이에 대한 식은 아래와 같다.
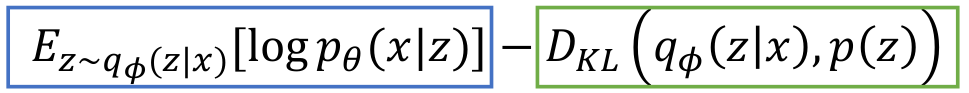 두가지 term은 서로 대립관계에 놓여서 학습된다.
두가지 term은 서로 대립관계에 놓여서 학습된다.
-
파란색 term : data reconstruction term
input data를 받아서 latent code를 생성하면, 이 latent code를 가지고 원래 data를 쉽게 reconstruct할 수 있게끔 한다. -
초록색 term : constraint
latent variables 의 distribution들이 simple하고 gaussian이게끔 한다. 이는 latent code에 constraint를 주는 것과 같다.
즉, 초록색 term은 latent code가 prior distribution처럼 최대한 간단하게끔 만들려고 하고,
파란색 term은 input data를 잘 reconstruct할 수 있도록 latent code가 최대한 충분한 정보를 갖고 있게끔 한다.
- 4번에서 구한 의 distribution에서 sampling하여 reconstruction을 구할 수 있다.
✅️ Summary
1.2) VAE : Generating Data
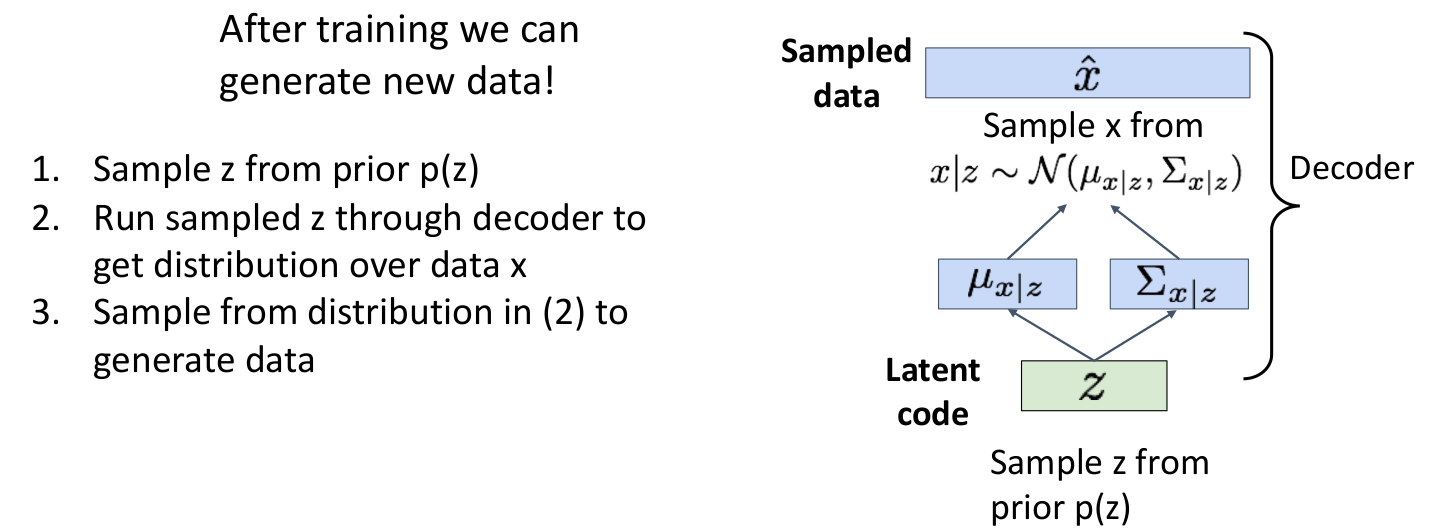 이제
이제 Decoder만을 사용하여 새로운 이미지를 생성할 수 있다.
- prior 에서 를 샘플링한다.
- 를
decoder에 통과시켜 새로운 에 대한 distribution을 얻는다. - 위에서 얻은 distribution으로부터 를 샘플링하여 새로운 이미지를 생성한다.
이는 Trainig 과정에서 학습한 이미지와 비슷한 새로운 이미지를 생성시킨다.
✅️ 생성 결과
 서로 다른 image dataset으로 학습시켰을 때 생성된 결과이다. 학습 데이터셋과 유사한 이미지를 생성하고 있다.
서로 다른 image dataset으로 학습시켰을 때 생성된 결과이다. 학습 데이터셋과 유사한 이미지를 생성하고 있다.
1.3) VAE : Editing with
 우리는 prior 를 Diagonal Gaussian distribution으로 가정하였기 때문에 이는 의 차원을 서로 독립적으로 만든다.
우리는 prior 를 Diagonal Gaussian distribution으로 가정하였기 때문에 이는 의 차원을 서로 독립적으로 만든다.
Disentangling factors of variation
- 가로축 를 보면 좌측은 7, 우측으로 갈수록 8 등으로 자연스럽게(smoothly) 변하는 것을 볼 수 있다.
- 세로축도 같은 양상을 확인할 수 있다.
- 따라서 이 를 변화시키면 모델이 생성하는 이미지를 조정할 수 있다.
✅️ Edit Images
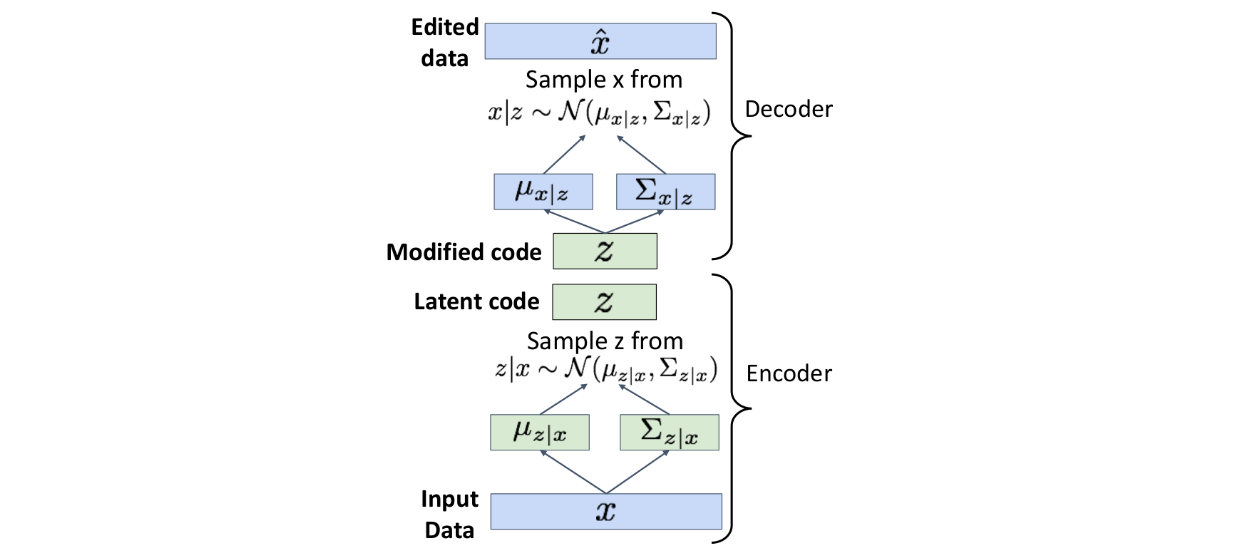
1. input data를 encoder에 통과시켜 latent codes의 distribution 를 얻는다.
- 위의 distribution에서 를 샘플링한다.
- 샘플링한 에서 몇몇 dimensions를 수정한다. (Modified code )
- Modified code 를
decoder에 통과시켜 새로운 에 대한 distribution을 얻는다. - 위의 distribution에서 새로운 를 샘플링하여 이미지를 생성한다.
 를 변형함으로써 얼굴의 표정이나 방향을 수정할 수 있다.
를 변형함으로써 얼굴의 표정이나 방향을 수정할 수 있다.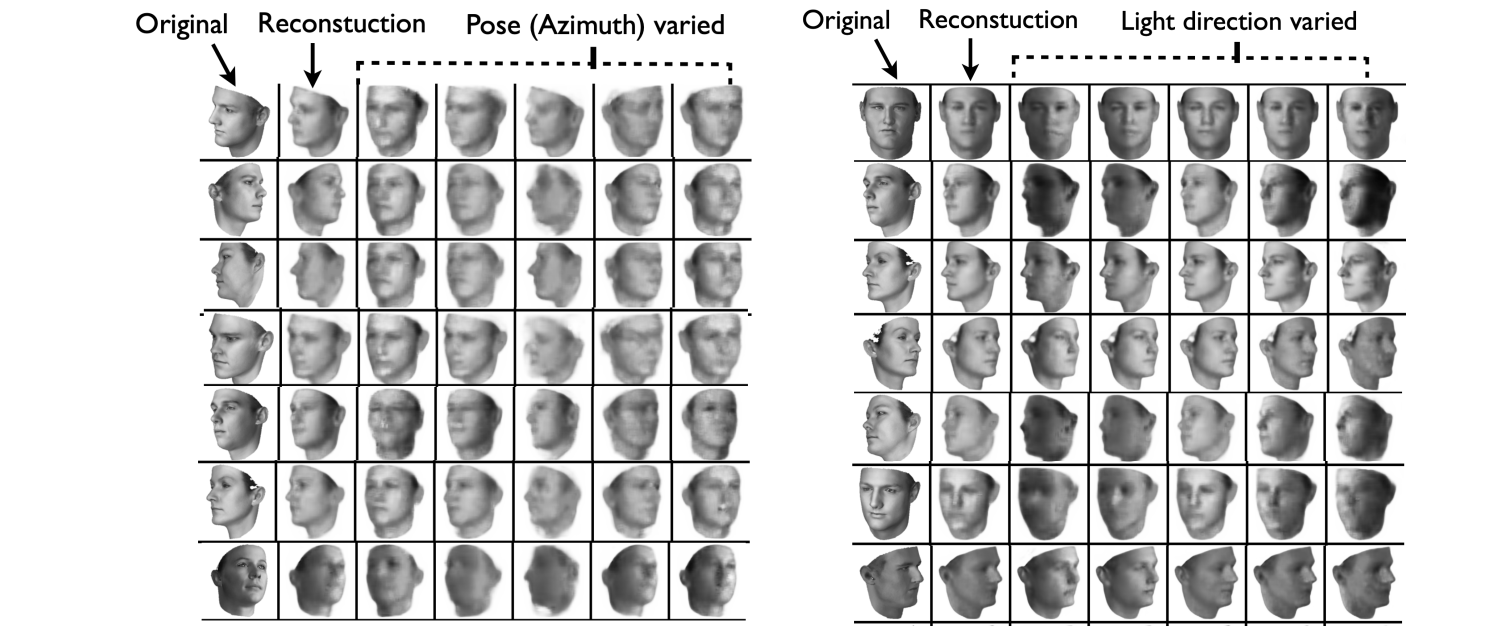
1.4) VAE : Summary

VAE는AE에 확률성을 집어넣음으로써 데이터의 생성이 가능하도록 하였다.
| 장점 | 단점 |
|---|---|
| Generative model의 원칙적인 접근방식이다. | likelihood의 lower bound를 최대화시키므로 실제 를 최대화시키는지 확신할 수 없다. 따라서 PixelRNN/PixelCNN에 비해 좋지 않다. |
| 를 추론하기 때문에 다른 task에 이 feature representation을 사용할 수 있다. | SOTA모델 GANs에 비해 블러리하고 낮은 퀄리티의 이미지를 생성한다. |
1.5) Autoregressive models vs Variational models

2. Vector-Quantized Variational Autoencoder (VQ-VAE2)
Autoregressive models와 Variational models는 각각의 장단점이 존재했다. 만약 이 둘을 합친다면?
Razavi et al, “Generating Diverse High-Fidelity Images with VQ-VAE-2”, NeurIPS 2019
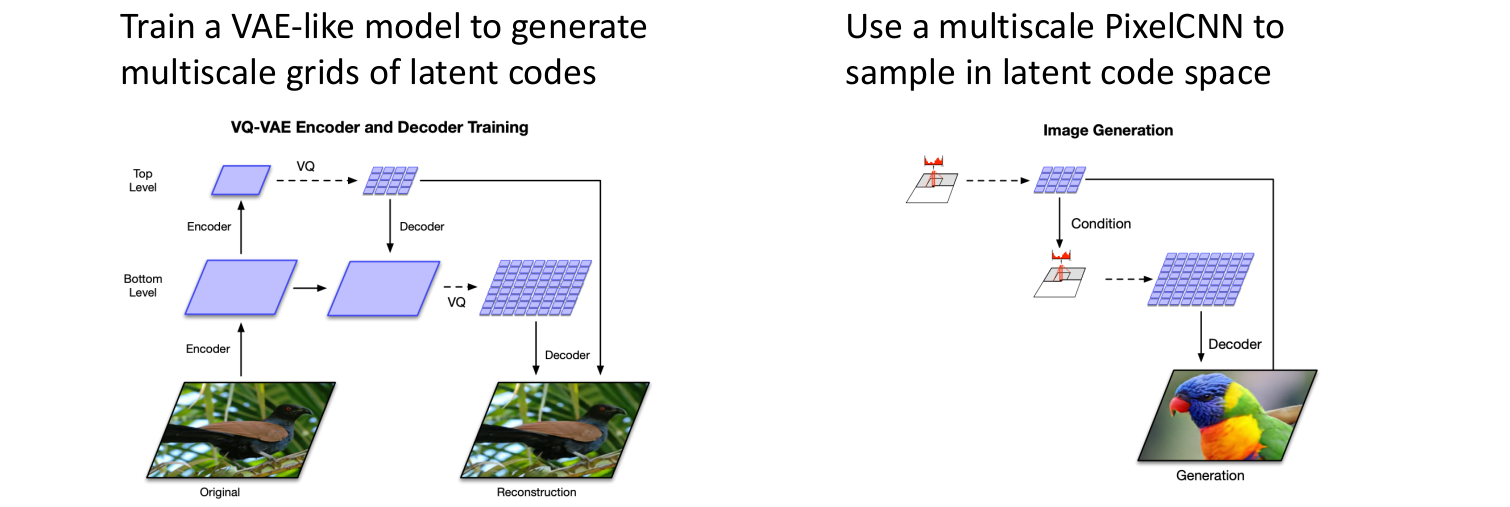
VAE모델을 학습시키는데 이때 latent vectors가 아니라 latent vectors의 multiscale grids를 학습한다.- 그리고
multiscale PixelCNN(Autoregressive model)을 사용하여 image space가 아니라 latent code space에서 샘플링한다.
VQ-VAE를 통해 매우 좋은 결과를 얻을 수 있다.


3. Autoregressive model, VAE, GANs Overview
| Models | 설명 |
|---|---|
| Autoregressive models | training data의 likelihood를 직접(directly) maximize한다. |
| VAE | latent 를 추가하였고, likelihood의 lower bound를 maximize한다. |
| GANs | 를 모델링하는 것을 포기한다. 그러나 로부터 샘플링할 수 있도록 한다. |
4. Generative Adversarial Networks
-
Setup
데이터들의 실제 distribution을 라고 하자.
그리고 우리의 학습 데이터들은 로부터 나온 라고 하자. -
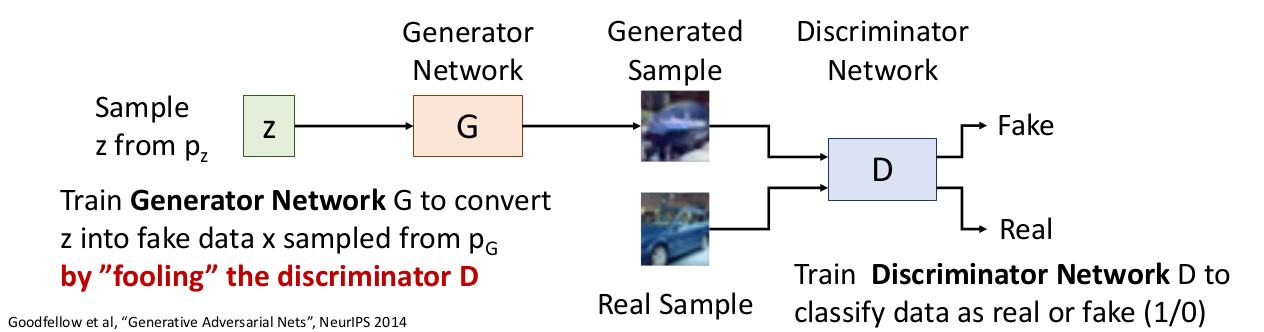
Idea
간단한 prior (diagonal gaussian, uniformed distribution 등)인 를 가진 latent variable 를 가정하자.
에서 를 샘플링하고 이를 Generative Network G에 통과시킨다.그렇다면 이 는 Generative distribution 에서 나온 것이다.
따라서 우리는 가 되기를 원한다. (실제 데이터들의 분포가 되기를 원함.)
-
Generator
로부터 를 샘플링하여 Discriminator이 에서 샘플링했다고 생각하도록 학습한다. -
Discriminator
생성된 샘플과 실제 샘플 사이에 real/fake(1/0)을 구분하도록 학습한다.
위 두 네트워크를 jointly하게 학습한다. 그렇게 된다면 가 로 converge될 것이다.
4.1) GANs : Training Objective
Generator G와 Discriminator D를 minimax game을 통해 jointly하게 학습시킨다.
수식을 더 자세히 살펴보면,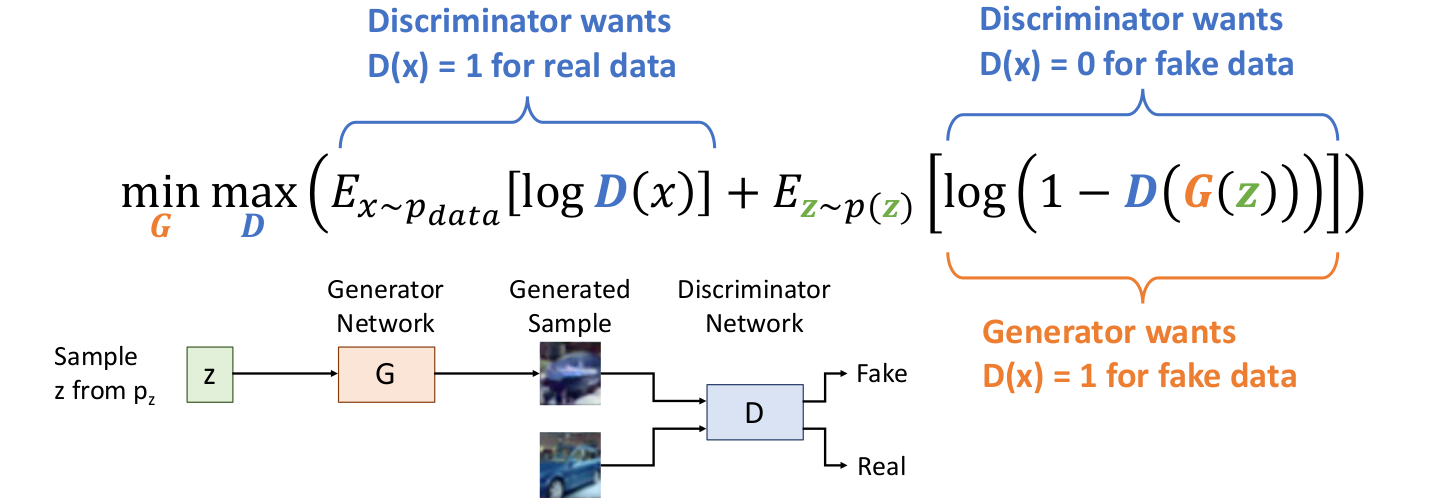
-
왼쪽 term
에서 샘플링한 , 즉 실제 data를 Real이라고 분류하도록 만드는 식이다.
이면 를 통과하여 매우 작은 음수가 되므로 이 되도록 학습하여 전체 식이 에 대해서 최대가 되도록 한다. -
오른쪽 term
에서 샘플링한 를 가지고 Generator G에 통과시킨 Generated sample 를 Discriminator D가 Fake라고 분류하도록 학습한다. 즉 생성된 이미지를 가짜라고 판별하도록.
Generator G는 Discriminator D가 를 Real이라고 분류하도록 학습한다. 즉 생성된 이미지가 진짜라고 판별되도록.
✅️ 학습과정과 문제점들
 수식의 편리성을 위해 식을 라고 하자.
수식의 편리성을 위해 식을 라고 하자.
우리는 G와 D를 alternating gradient updates를 통해 학습시킨다.
-
D에 대한 미분을 통해 Gradient ascent로 D에 대해서 식을 maximize시킨다.
-
G에 대한 미분을 통해 Gradient descent로 G에 대해서 식을 minimize시킨다.
-
그리고 1, 2 과정을 T번 반복한다.
-
문제점 1
그러나 D에 대해서는 maximize, G에 대해서는 minimize시키며
전체 loss가 없이 각각에 대한 loss값이 주어진다. 따라서 우리는 전체 loss를 최소화시키는 것이 아니다!
만약 D가 매우 잘 학습이 되었다면, G는 매우 안 좋을 것이다. 이 상태라면 D에 대해서는 낮은 loss를 가질 것이고 G에 대해서는 높은 loss를 가질 것이다.일반적인 전체 loss가 아래로 우하향하는 그래프로 주어지는 것이 아니라,
G와 D가 결합되어 불규칙한 전체 loss값이 나오는 그래프로 나올 것이다. -
문제점 2
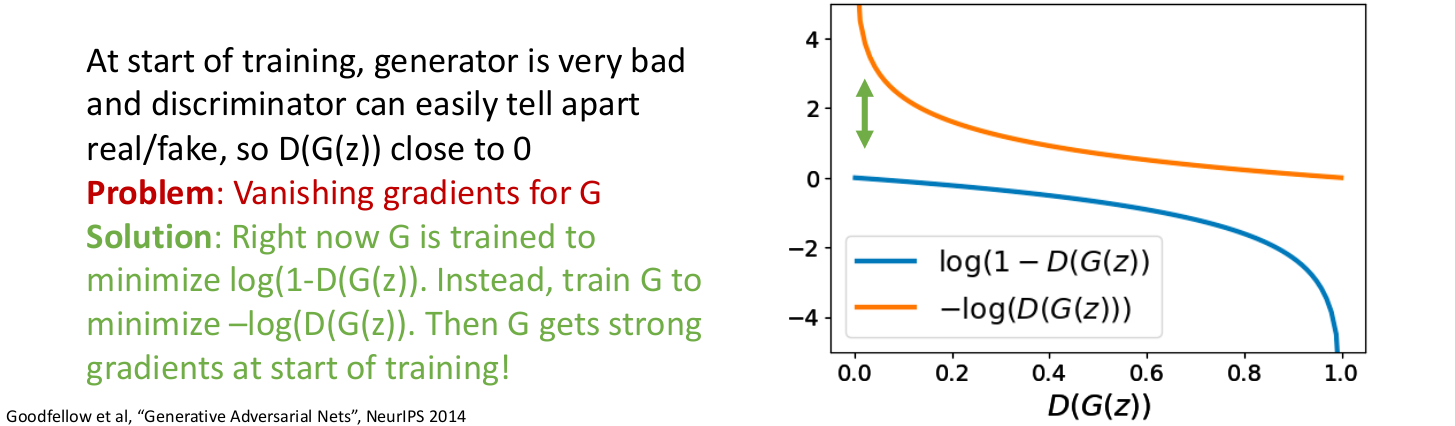 식의 오른쪽 term에서
식의 오른쪽 term에서을 그래프로 그려보면 위의 파란색 그래프와 같다.
학습 초반에는 Generator이 안 좋을 것이므로 가 0에 가까울 것인데, 이러면 이때의 그래프가 평평하여 Vanishing Gradients문제가 발생한다.이를 해결하기 위해 minimize 대신에
minimize 를 사용한다.
이러면 학습 초반에 강한 gradients를 얻을 수 있다.
4.2) GANs : Optimality
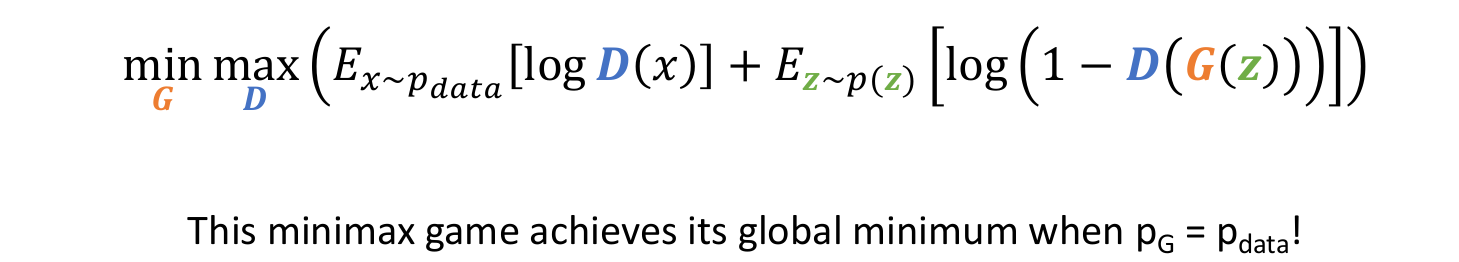 우리의 minimax game은 를 만족할 때 global minimum에 도달한다.
우리의 minimax game은 를 만족할 때 global minimum에 도달한다.
그렇다면 어떻게...
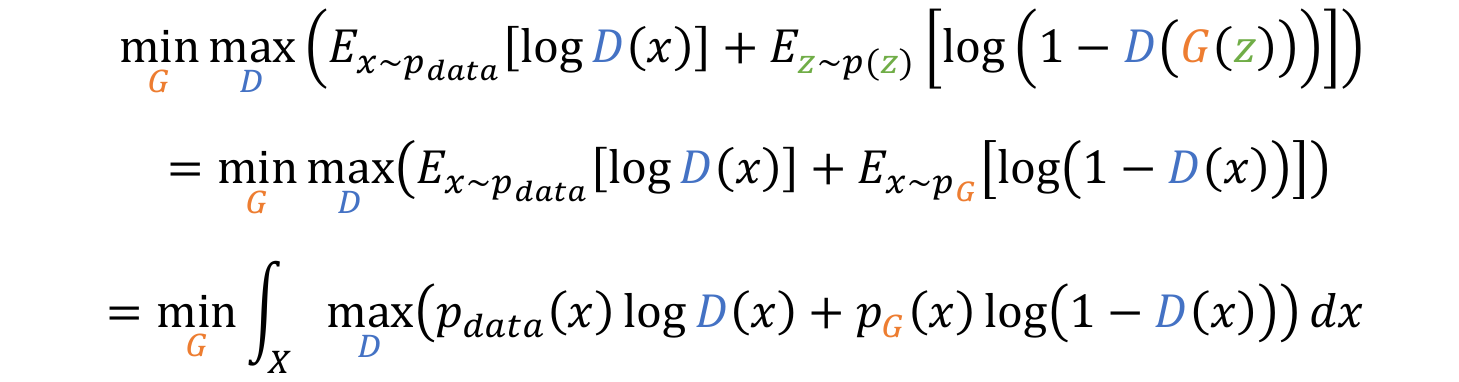
- 먼저 생성된 를 에서의 로 변수를 바꾼다.
- Expectation의 정의에 따라 integral형식으로 식을 변환한다. (?이부분 잘 모르겠음. 수학공부하자..)
- term을 integral 안으로 이동시킨다.
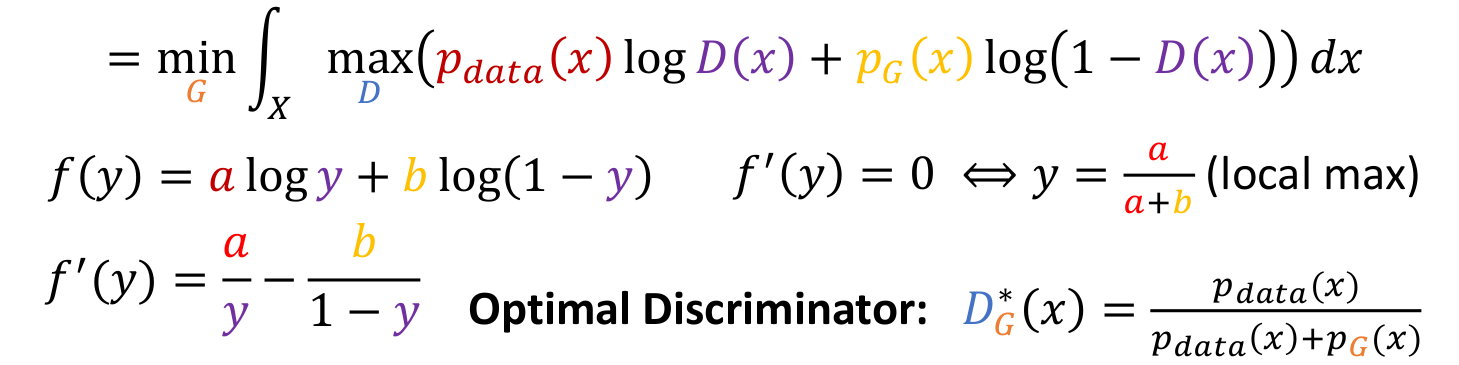
- 그러면 위의 식이 의 형태인 것을 알 수 있다.
- 그리고 우리는 인 값도 구할 수 있다.
- 이 값은 Optimal Discriminator 값이지만, 우리는 를 계산할 수 없다.. 하지만 우리는 이 값이 Optimal Solution이라는 것을 알고 이를 활용할 것이다.
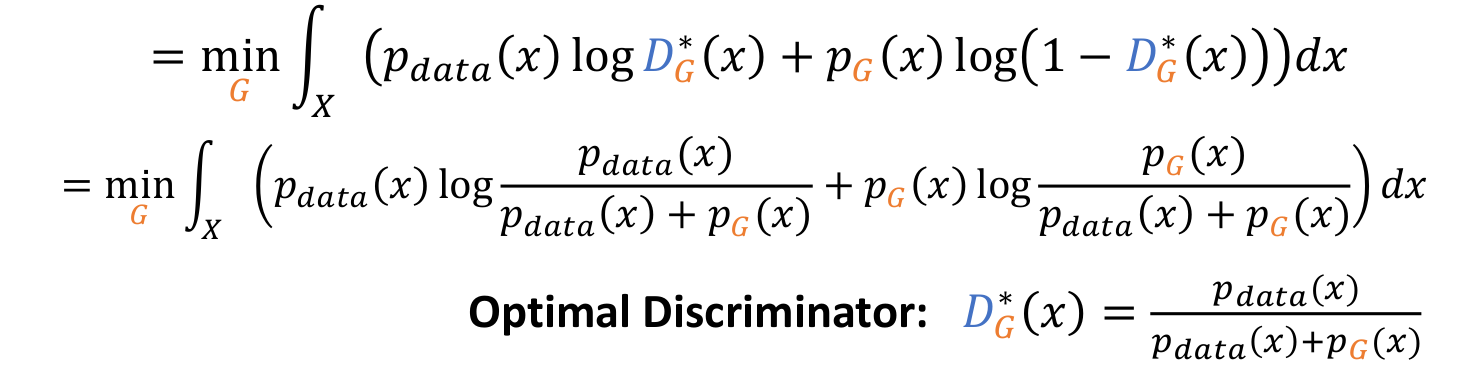
- 를 Optimal solution인 로 교체하여 term을 없앤다.
- 그리고 에 그 값을 대입시킨다.
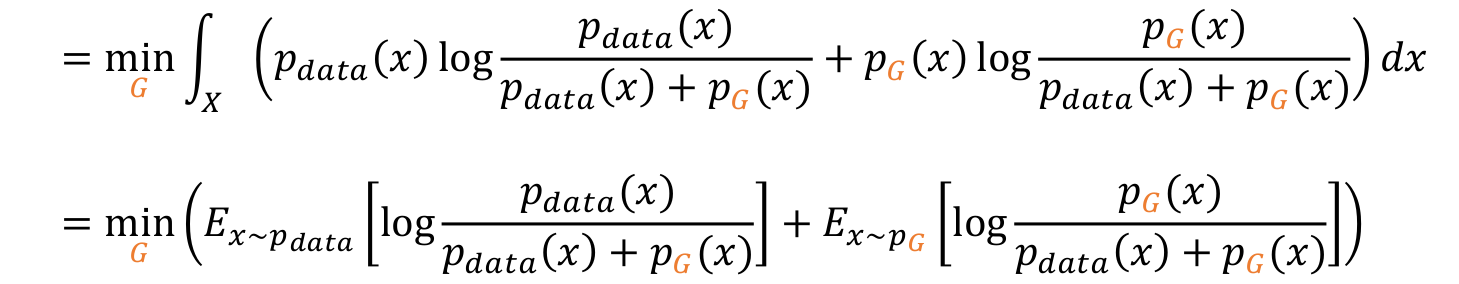
- Expectation의 정의대로 integral을 다시 변형시킨다.
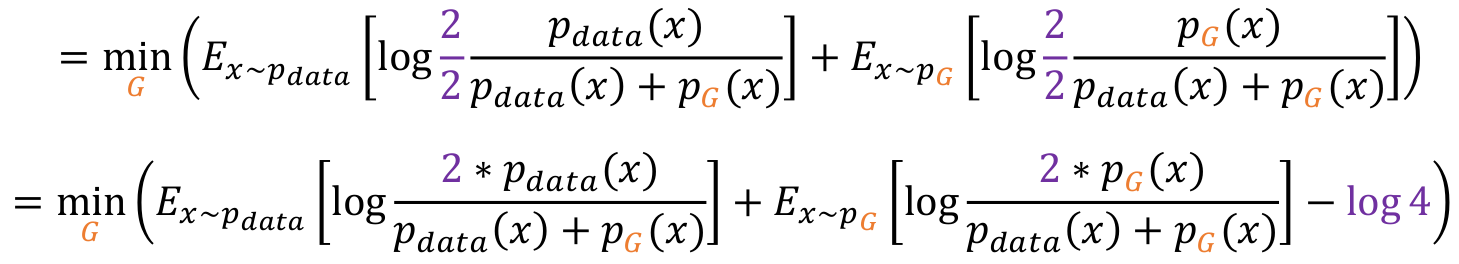
- 분자, 분모에 각각 2를 곱해준다.

- 그러면 KL Divergence의 형태가 되어 KL식으로 변형할 수 있다.
- KL Divergence는 distribution과 distribution사이의 거리를 측정하는 계산식이다.
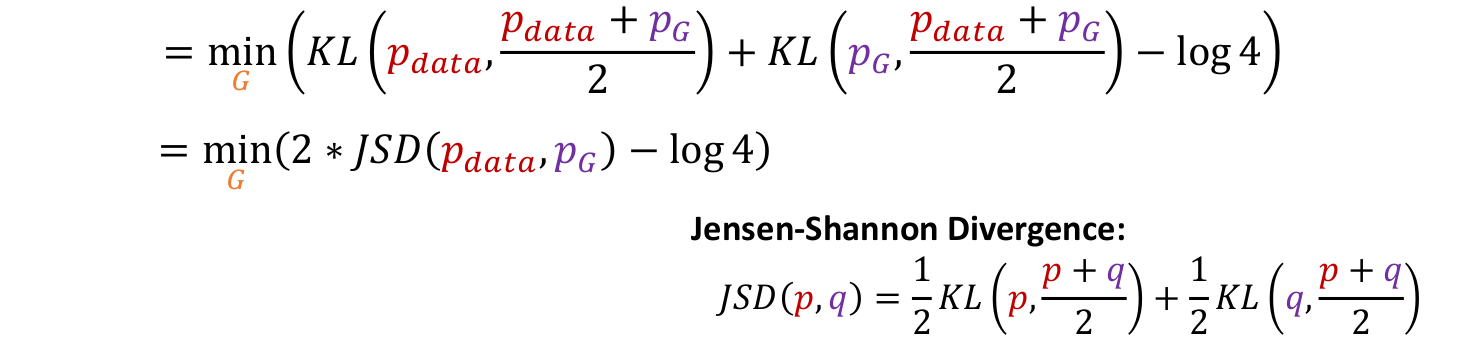
- 이는 다시 Jensen-Shannon Divergence의 형태가 되어 JSD연산으로 교체할 수 있다.
minmax game이었던 식을 최종적으로 의 식으로 변형하여 optimize할 수 있다.
JSD는 항상 0이상의 값을 가지며, 0의 값을 가지는 경우는 두 distribution이 같을 때이므로, 일 때가 global minimum임을 확인할 수 있다.
✅️ Summary
 Global minimum은
Global minimum은
- 이고,
- 일때 발생한다.
그러나
- G, D는 정해진 Neural network이므로, 이 네트워크가 Optimal solution으로 이끌지는 모른다. 즉, 가 되도록 를 represent할 수 있을지 모른다.
- 그리고 Optimal solution으로 converge될지도 모른다.
✅️ Results

4.3) GANs : DC-GAN
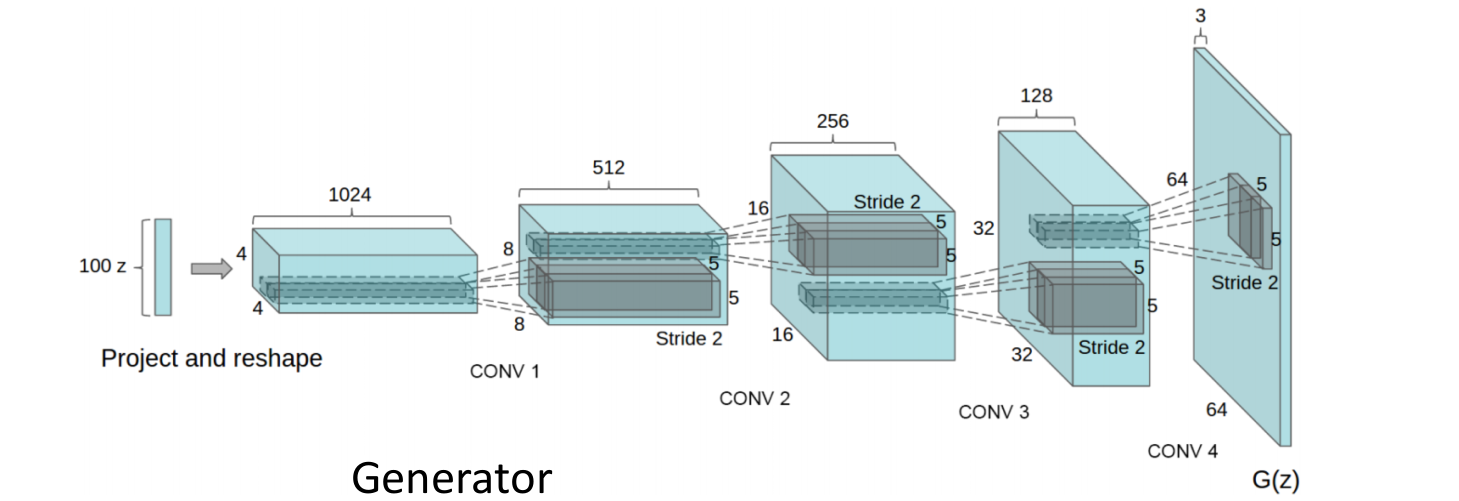
- Generator와 Discriminator를 5개의 Conv를 사용한 아키텍쳐로 설정하였다.

- 침대 사진으로 학습시킨 모델의 결과이다.

- 또한, 여러
latent vector z를 linearly interpolate하여 non-trivial solution을 얻을 수 있다. (여러 침대가 합쳐지는.??)
4.4) GANs : Vector Math

- Generated images를 종류별로 분류하여 각 카테고리에 사용된
latent vector z들을 Average한다. - 그리고 이들에 대해 +, - 연산을 진행하여 각 카테고리가 가지고 있는 특징들을 더하고 뺄 수 있다.
- 위 사진은 웃는 여자 - 웃지 않는 여자 + 웃지 않는 남자 = 웃는 남자 를 보이고 있다.

- 안경쓴 남자 - 안경안쓴 남자 + 안경안쓴 여자 = 안경쓴 여자
4.5) GAN Improvments
매우 많은 GAN 논문들이 나오고 있는 상황이다.
✅️ Improved loss functions

- GAN loss function을 변형하여 더 좋은 결과를 내었다.
✅️ Higher resolution

Progressive GAN

Style GAN- latent vector을 interpolate하여 자연스럽게 스타일을 변형할 수 있다.
- https://drive.google.com/drive/folders/1NFO7_vH0t98J13ckJYFd7kuaTkyeRJ86
5. Conditional GANs
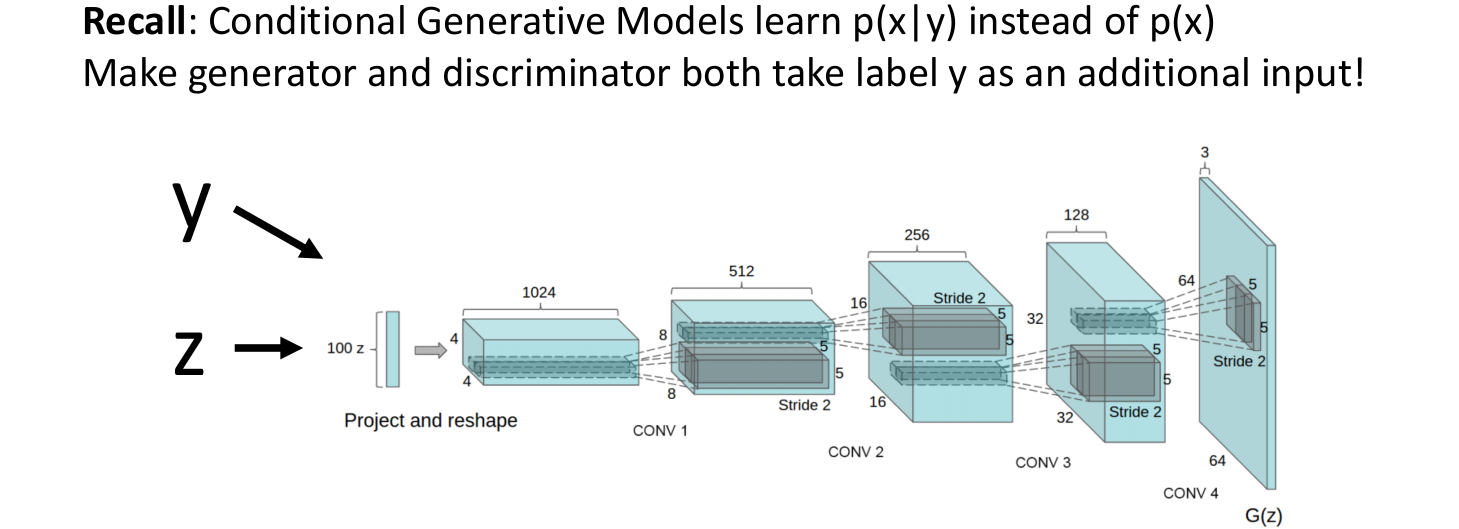
- 기존의 GAN은 training datasets로 학습시키고 그와 비슷한 새로운 data를 무작위로 생성한다.
- Conditional GAN은 우리가 어떤 카테고리의 이미지를 생성할지 정할 수 있다.
- 이를 위해 카테고리를 나타내는 label y를 input으로 추가한다.
5.1) Conditional Batch Normalization
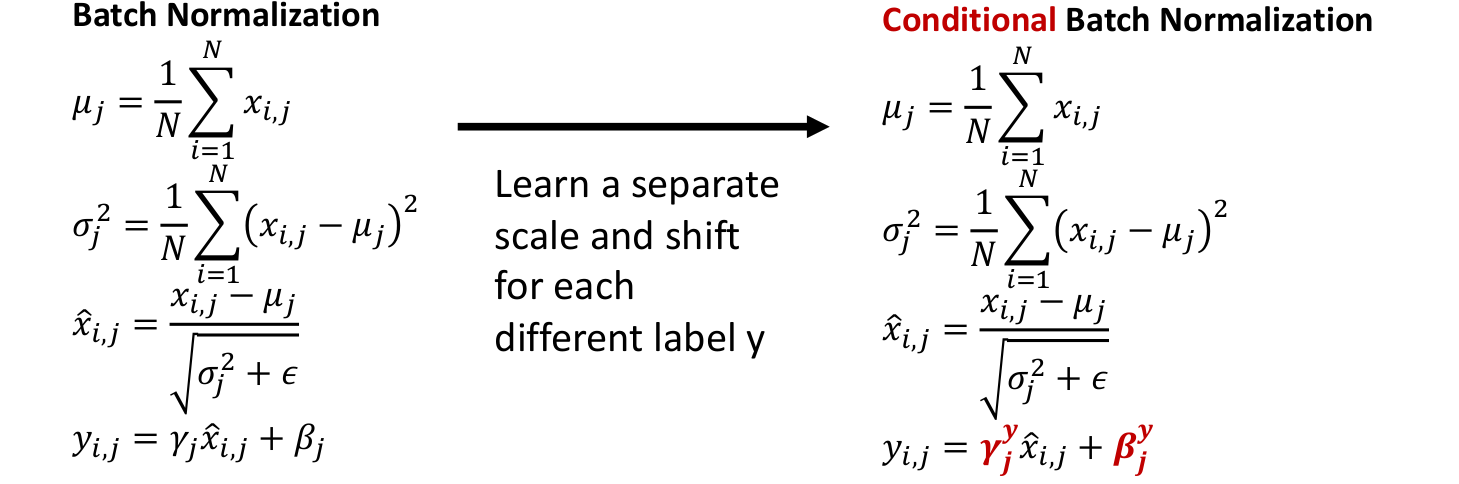
- 기존 Batch Norm에 비해, 다른 label을 나타낼 수 있도록 에 label을 추가한다.
- 이를 통해 test time에 우리가 label을 주면 그에 맞는 이미지를 생성할 수 있다.
5.2) Spectral Normalization

- Spectral Norm을 사용하여 label에 맞는 이미지를 생성하는 모델.
5.3) Self-Attention

- Self-Attention을 통해서도 이미지 label을 잘 학습하는 것을 알 수 있다.
5.4) BigGAN

- 2019년 당시 SOTA모델이었다. Justin Johnson이 GAN에서 꼭 읽어보라는 논문이다.
5.5) Generating Videos with GANs

- GAN을 사용하여 비디오를 생성할 수도 있다.
5.6) Conditioning on more than labels! Text to Image

- 이미지 label y가 아니라 더욱 복잡한 Text를 주어 이미지를 생성한다.
- 문장 y를 주면 그에 맞는이미지를 생성한다.
5.7) Image Super-Resolution: Low-Res to High-Res

- 자기 자신 이미지를 y로 주어 Resulolution을 upsampling할 수 있다.
5.8) Image-to-Image Translation: Pix2Pix
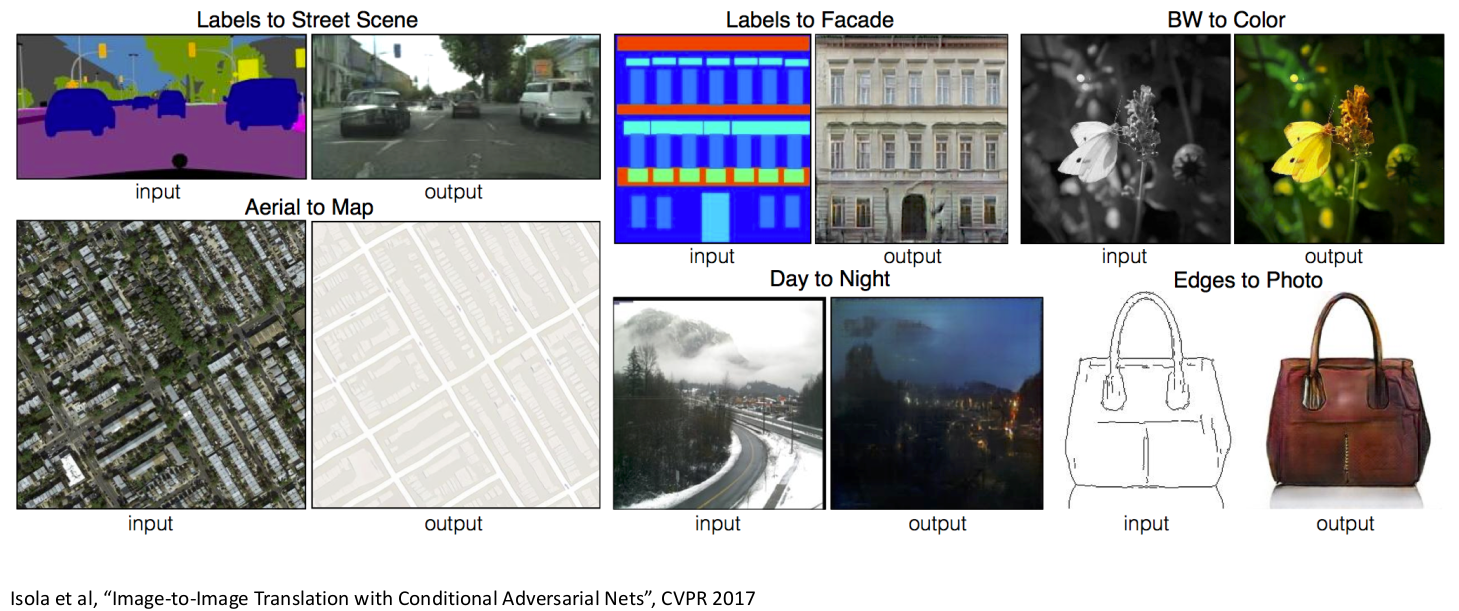
- 이미지를 다른형태의 이미지로 변형할 수 있다.
5.9) Unpaired Image-to-Image Translation: CycleGAN


- unpaird horse, zebra 이미지에 대해서도 각 특징들을 전환시킬 수 있다.
5.10) Label Map to Image

- 두개의 y를 input으로 사용한다.
- semantic map과 style을 합칠 수 있다.
5.11) GANs: Not just for images! Trajectory Prediction
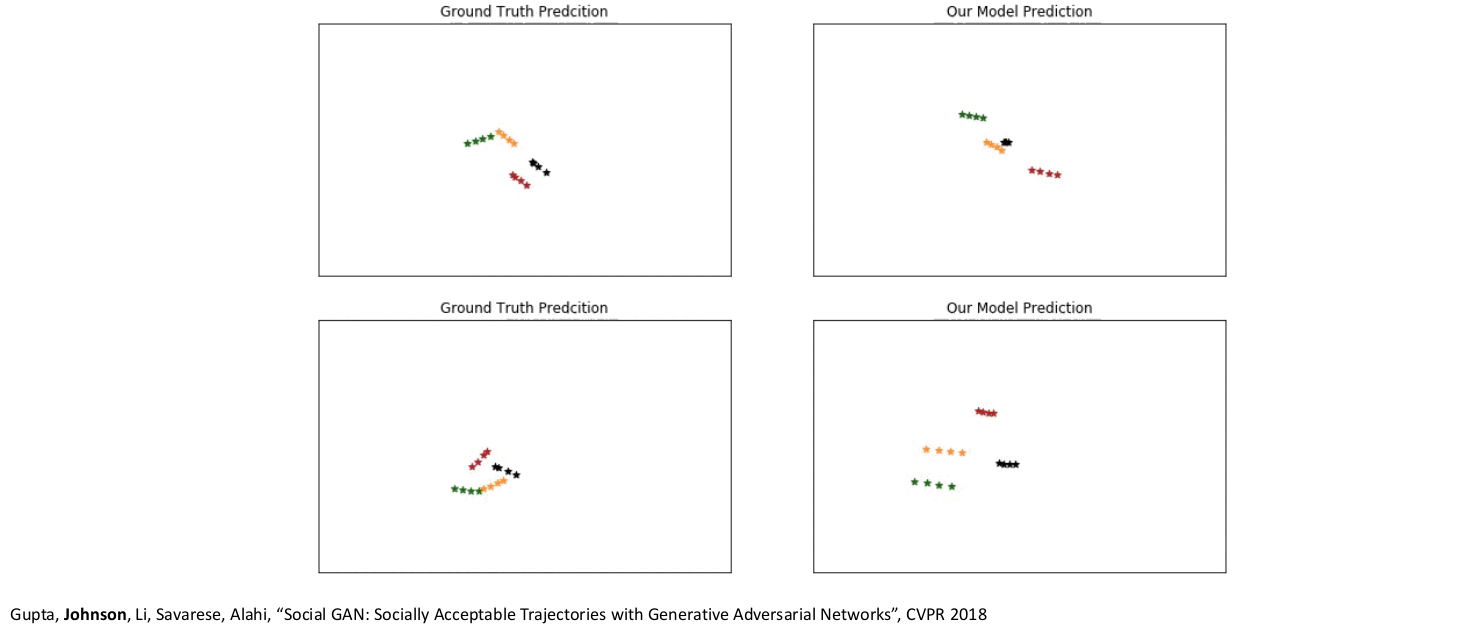
- 사람들의 이전 이동경로를 y로 input시키고, 미래의 이동지점을 예측하여 생성한다.
6. Generative Models Summary


유익해요~