Generative Models I

---

1. Supervised Learning vs Unsupervised Learning
2. Discriminative vs Generative Models
   2.1) 위 Models을 가지고 무엇을 할 수 있을까
   2.2) Taxonomy of Generative Models
3. Autoregressive Models
   3.1) Explicit Density Estimation
   3.2) Explicit Density: Autoregressive Models
   3.3) PixelRNN
   3.4) PixelCNN
   3.5) 결과 및 결론
4. Variational Autoencoders
   4.1) (Regular, non-variational) Autoencoders
   4.2) Variational Autoencoders Overview
   4.3) Variational Autoencoders

---

1. Supervised Learning vs Unsupervised Learning

	Supervised Learning	Unsupervised Learning
Data	$(x, y):\ x\text{ is data},\ y\text{ is label}$	$x$
Goal	$x\rightarrow y$ 로 가는 function을 학습	Learn some underlying hidden structure of the data
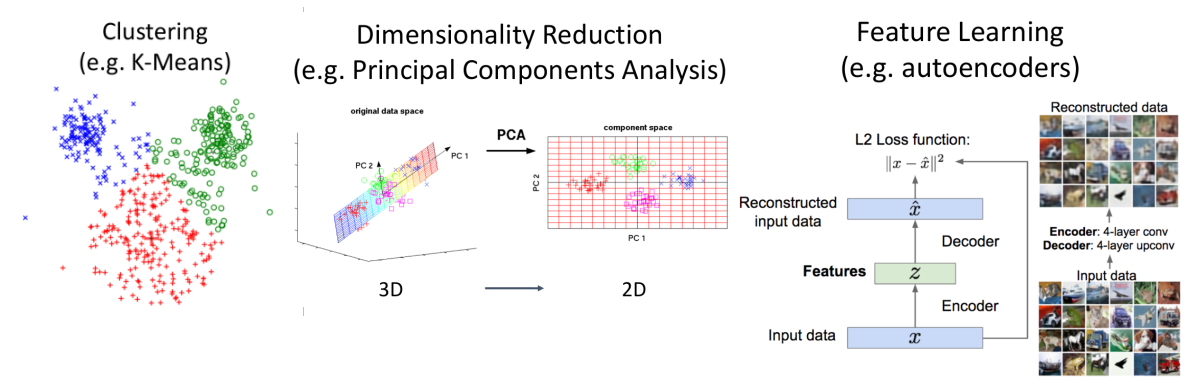
Examples	Classification, regression, object detection, semantic segmantation, image captioning, etc.	Clustering, dimensionality reduction, feature learning, density estimation, etc.

• Unsupervised Learning 예시

---

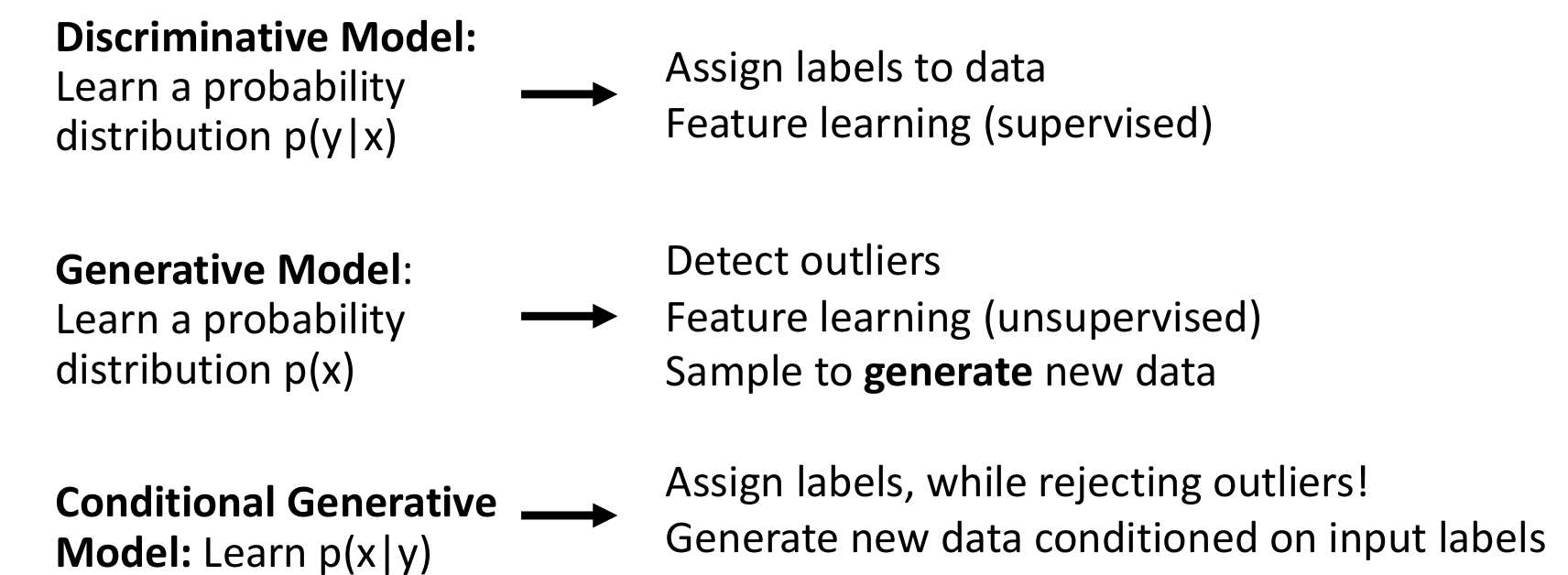
2. Discriminative vs Generative Models

---

Density Function

$p(x)$ 는 각 가능한 $x$에 대해 양의 값을 가진다. 더 클수록 $x$가 더 그럴듯 하다.
Density Functions는 nomalized되어있다:

확률의 합이 1이 되므로 만약 하나의 확률이 크다면 다른 확률들은 줄어들게 된다. (compete each other)

---

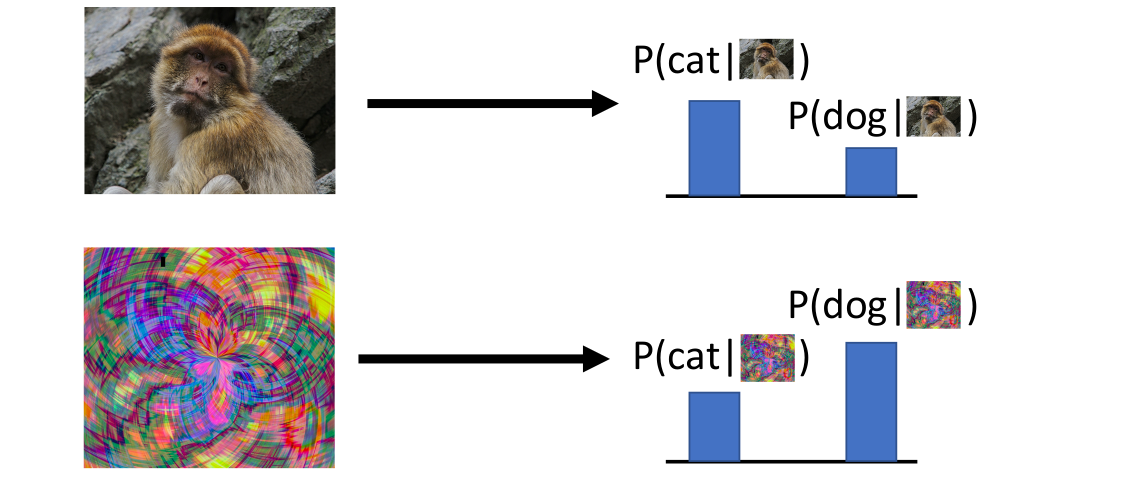
• ✅️ Discriminative Model

  Learn a probability distribution $p(y|x)$ that predicts probability of the label $y$ conditioned on the input image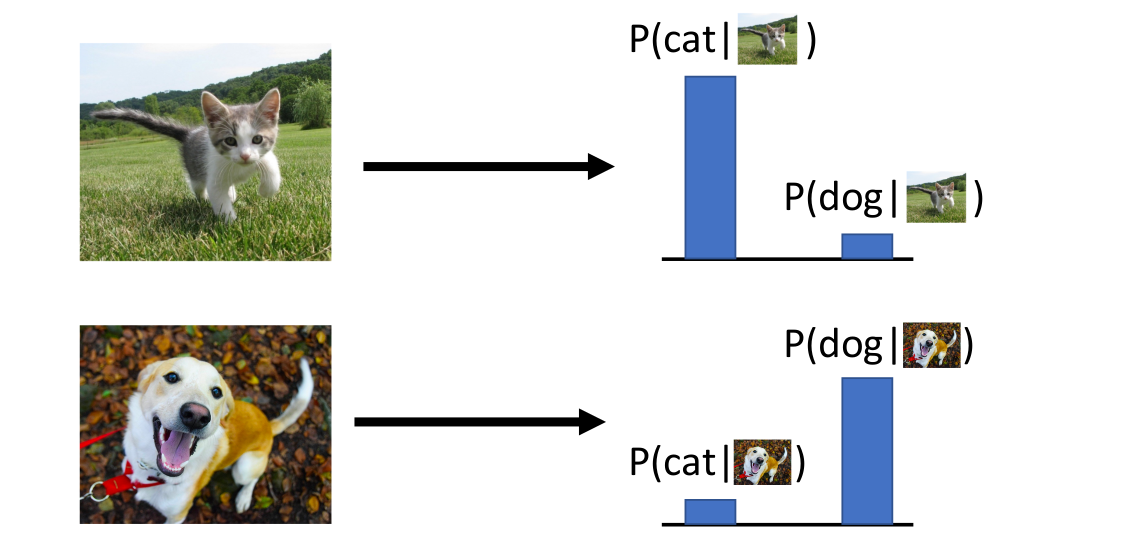 $x$

  • input $x$를 입력받아서 그에 대한 label이 나올 확률을 구한다.

  • 각 input에 대한 가능한 labels사이에서 probability에 대해 compete한다.

  • 그러나 input images 사이에서는 compete하지 않는다.

    

  • 정해놓은 labels와 다른 input이 주어져도 확률을 계산한다.

• ✅️ Generative Model

  Learn a probability distribution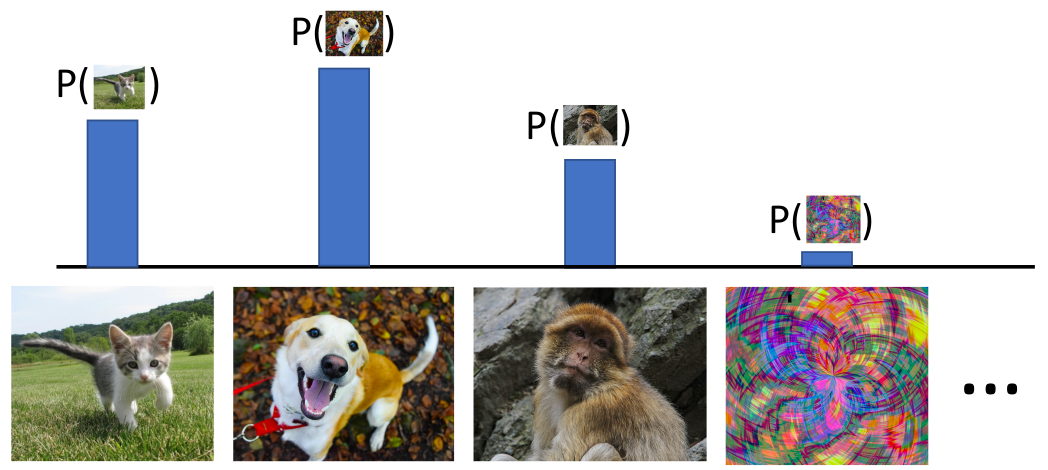 $p(x)$
  • 모든 가능한 images가 probability mass에 대해 compete한다.
  • 이미지에 대한 깊은 이해가 필요하다. (개가 앉은것 vs 일어선 것 중 어느 것이 더 그럴듯한가?)
  • 모델은 불합리적인 inputs에 매우 작은 값을 부여하여 reject할 수 있다.

• ✅️ Conditional Generative Model

  Learn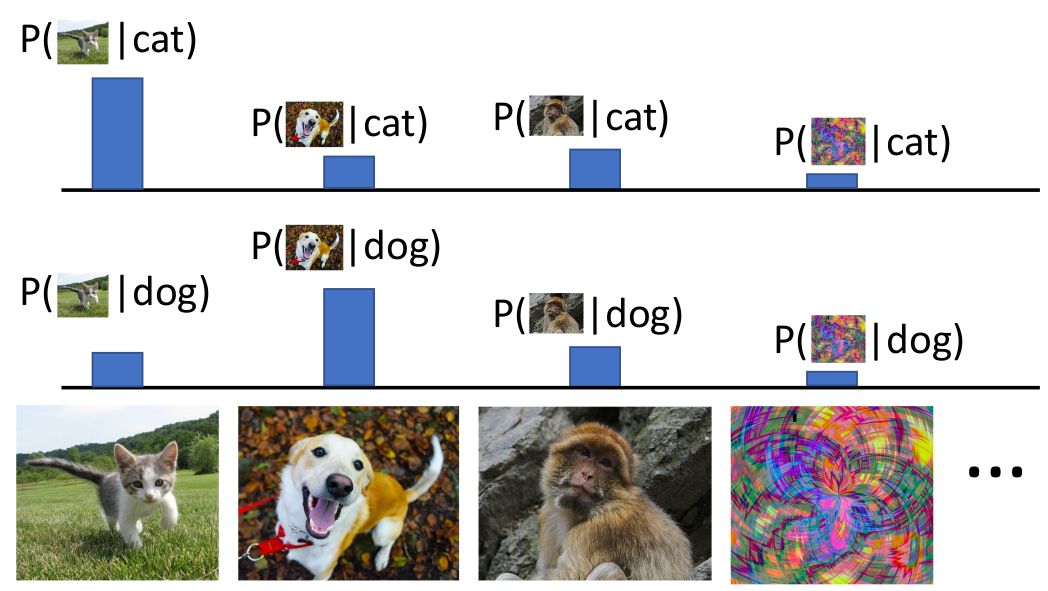 $p(x|y)$

2.1) 위 Models을 가지고 무엇을 할 수 있을까

2.2) Taxonomy of Generative Models

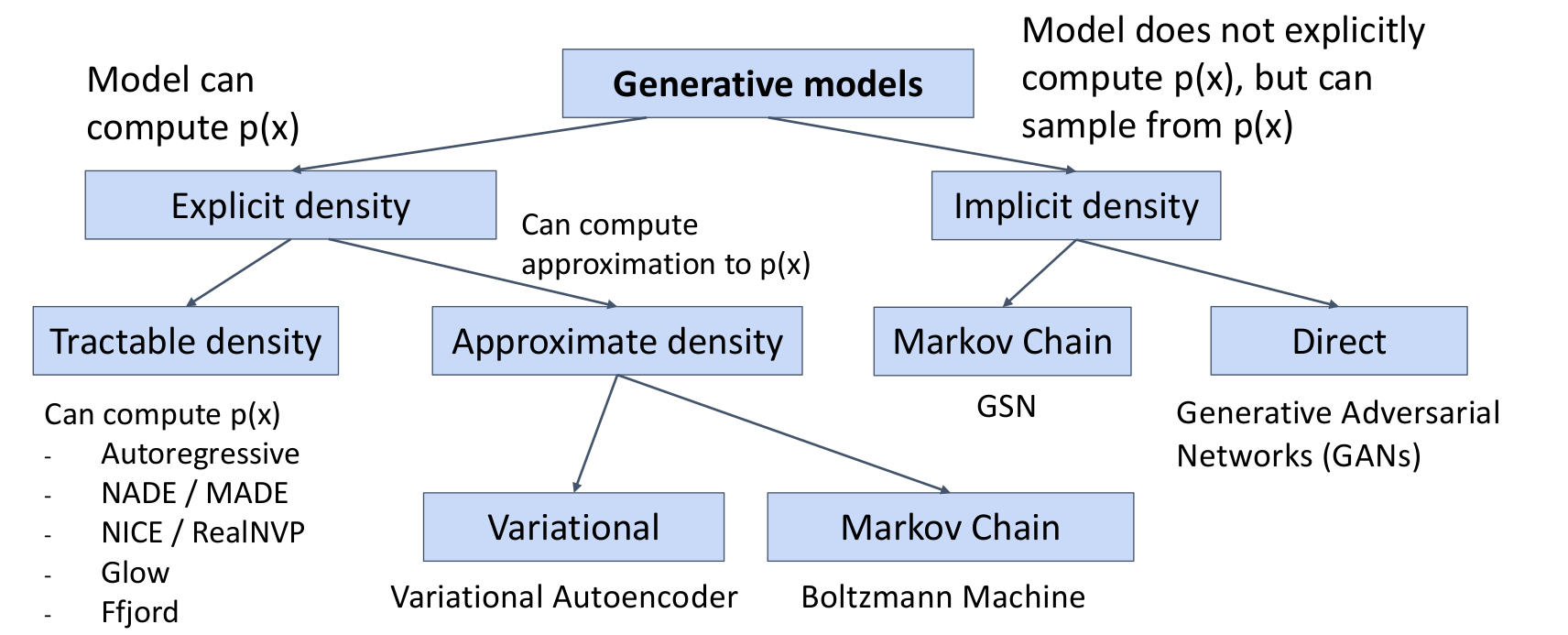
• Explicit density : desity function $p(x)$을 계산한다.

  • Tractable density
  • Approximate density : $p(x)$를 근사한다.
    • Variational
    • Markov Chain

• Implicit density : $p(x)$를 계산하지는 않지만 $p(x)$로부터 샘플링한다. ($p(x)$의 값을 얻을 수는 없다. $p(x)$가 큰 값을 가지는 것에서 샘플링한다.)

  • Markov Chain
  • Direct

---

3. Autoregressive Models

3.1) Explicit Density Estimation

Goal : Write down an explicit function for $p(x)=f(x,W)\\ \ x:\text{data},\ W:\text{learnable weight matrix}$

$x^{(1)}, x^{(2)},..., x^{(N)}$ 의 dataset이 주어졌을 때, 아래의 식을 해결하여 모델을 학습한다.

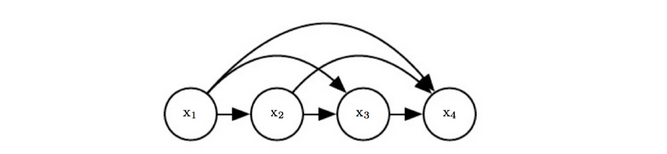
3.2) Explicit Density: Autoregressive Models

자기 자신을 입력으로 하여 자기 자신을 예측하는 모형 (출처)

• $x$가 여러 subparts로 이루어져있다고 가정한다. $x$가 이미지라고 하면, subparts는 각 픽셀이다.
  $x=(x_1, x_2, x_3,...,x_T)$
• chainrool을 사용하여 probability를 계산한다.
  $\begin{aligned}p(x)&=p(x_1,x_2,...,x_T)\\ &=p(x_1)\ p(x_2|x_1)\ p(x_3|x_1,x_2)\\ &=\prod_{t=1}^Tp(x_t|x_1,...,x_{t-1}) \end{aligned}$
  즉, sequence의 확률 $p(x)$는 이전 sequence가 주어졌을 때 다음 sequence가 나올 확률을 전부 곱한 것이다.
  대체 무엇이 probability distribution이고 어떻게 계산이 된다는 것인지 개념이 잘 이해가 안간다면 이 링크를 보고 다시 깨우보자..

이는 이전 subparts를 모두 가지고 다음 subpart를 계산하는 RNN모델과 유사하다.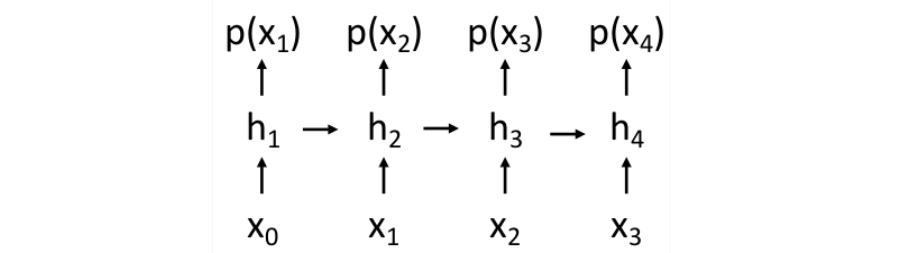

3.3) PixelRNN

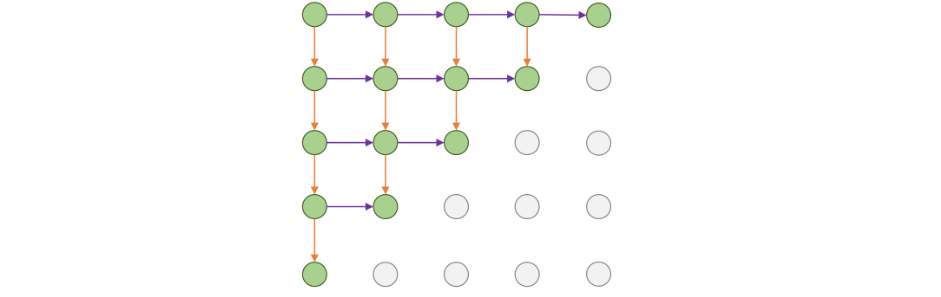왼쪽 위의 pixel에서부터 시작하여 RNN을 통해 한번에 하나의 pixel을 생성한다.

각 pixel의 hidden state는 왼쪽과 위쪽의 hidden state와 RGB values에 의존한다.

그리고 channel은 R, G, B의 순서로 정의하여 계산한다. (출처)

그러나 NxN이미지는 2N-1의 sequential steps를 필요로 하므로 training과 testing에서 모두 매우 느리다.

3.4) PixelCNN

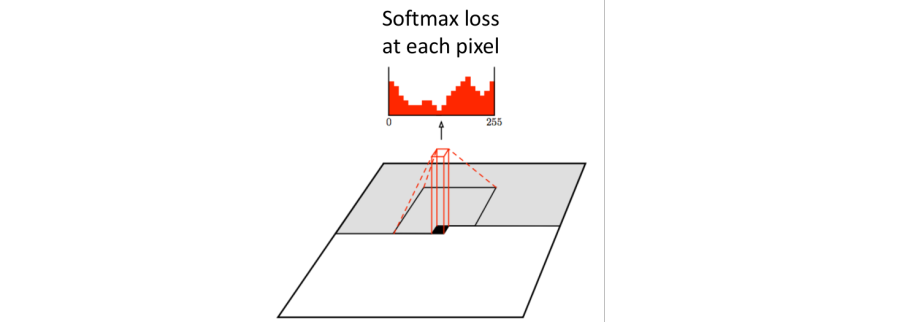이전 pixel들로부터 의존성을 가져오기 위해 convolution을 사용한다. PixelRNN에서처럼 왼쪽 위 pixel에서 시작하여 하나하나 pixel을 생성한다.

그러나 미래 정보를 반영하면 안되기 때문에 convolution연산에 반영하지 않을 부분에 0을 곱해서 제외한다.

PixelRNN보다 Training시 더 빠르다.(Training 이미지에서 context region 이후의 값들을 알기 때문에 convolution을 병렬계산할 수 있다.

그러나 Generation 시에는 sequential하게 작동하므로 여전히 느리다.

3.5) 결과 및 결론

위 사진은 PixelRNN으로 생성한 이미지이다.

• 겉으로 보기에는 합리적으로 보이지만 사실 자세히 보면 거지같다..
• 그래도 edges, colors를 꽤나 그럴싸하게 생성하는 것에 의의를 가진다.
• 이는 unconditional generation이므로 test time에 내가 무엇을 생성하고 있는지 정할 수 없다.

✅️ Autoregressive Models 장단점

• Pros
  • Likelihood $p(x)$를 명시적으로 계산할 수 있다.
  • 위의 장점 덕분에 좋은 evaluation metric을 얻는다. (training data와 유사한, 즉 얼마나 그럴듯한지에 대한 $p(x)$ 값을 얻을 수 있기 때문이다.)
  • 나름 괜찮은 결과를 얻을 수 있다. (진짜 사진같지는 않지만..)
• Cons
  • Sequential Generation 이므로 느리다.

---

4. Variational Autoencoders

PixelRNN과 PixelCNN에서는 parametric densitiy function $p(x)=f(x,W)$을 정의하여 각 input에 대해 계산하고 각 input에 대해 값을 최대화하도록 학습하였다.

VAE에서는 실제 density 값을 최대화하는 대신, density의 lower bound를 최대화시킨다.

4.1) (Regular, non-variational) Autoencoders

Unsupervised method로, labels 없이 raw data $x$로부터 feature vectors를 학습한다.
Unsupervised method for learning feature vectors from raw data x, without any labels

• Features는 downstream tasks에 활용할 수 있는 유용한 정보를 추출한다.

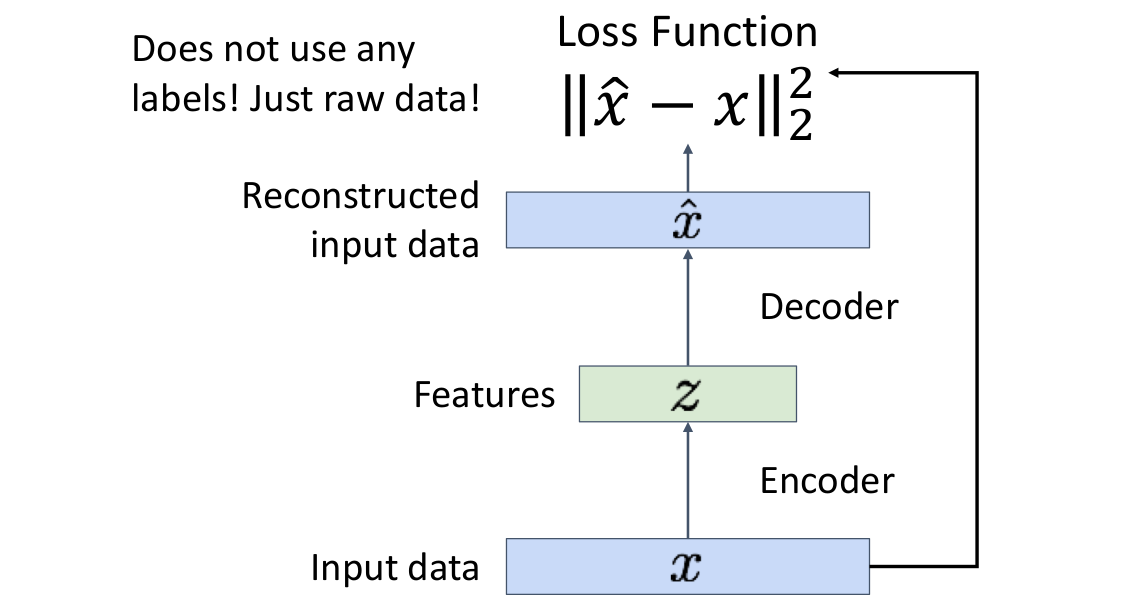
• Encoder을 통해 input data에서 추출한 features를 사용하여

• Decoder을 통해 다시 input data를 reconstruct한다.

• Encoder은

  • Originally: Linear + nonlinearity (sigmoid)
  • Later: Deep, fully-connected
  • Later: ReLU CNN (upconv)

  로 이루어져 있다.

우리는 Encoder을 통해 input data를 압축 (lower dimension)하는 효과를 기대한다.

• 학습을 마친 후, decoder을 버리고, encoder을 사용하여 downstream task에 사용한다.
• Not probabilistic : 학습하지 않은 new data를 sampling할 수 없다.

4.2) Variational Autoencoders Overview

처음 보면 이해가 매우 힘든 개념이라서 다시 볼 때도 (출처)를 읽어서 이해하려고 해보자..

Autoencoder에 확률 개념을 도입하였다
1. raw data로부터 latent features $z$를 학습한다.
2. new data를 생성하기 위해 model로부터 sampling한다.

✅️ 기본개념

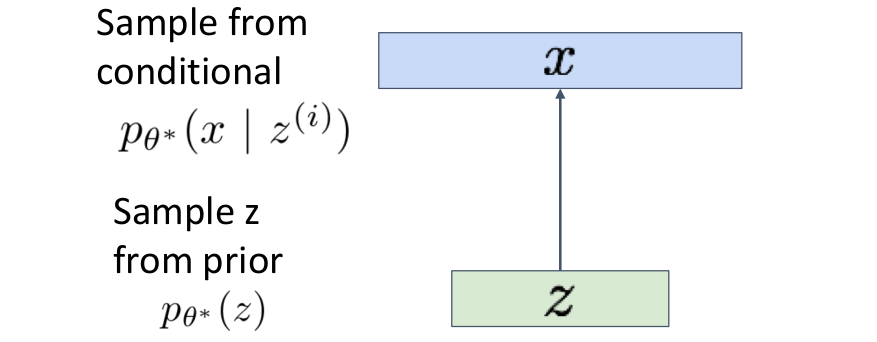latent features $z$로부터 input data와 유사하지만 완전히 새로운 data인 $x$를 생성하는 과정이다. (Decoder부분이다.)
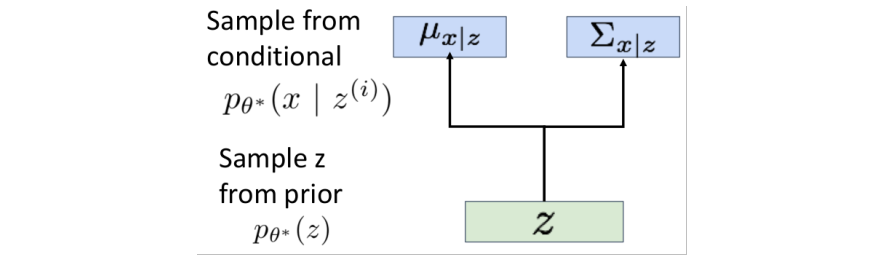
prior distribution $p_{\theta*}(z)$에서 latent variable을 sample하고, sampling한 $z$를 decoder에 넣어서 image $x$를 predict한다. 이때 output은 single image가 아니라 images에 대한 distribution이다.

---

$p_{\theta*}(z)$ : prior distribution으로 $z$의 확률밀도함수이다. 가우시안을 따른다고 가정한다.
$p_{\theta*}(x|z^{(i)})$ : 주어진 $z$에서 특정 $x$가 나올 조건부 확률에 대한 확률밀도함수
$\theta$ : 파라미터

---

VAE에서의 $z$는 AE에서의 $z$(a value: low dimension of input data)와 다르게,
가우시안 확률분포에 기반한 확률값으로 나타낸다.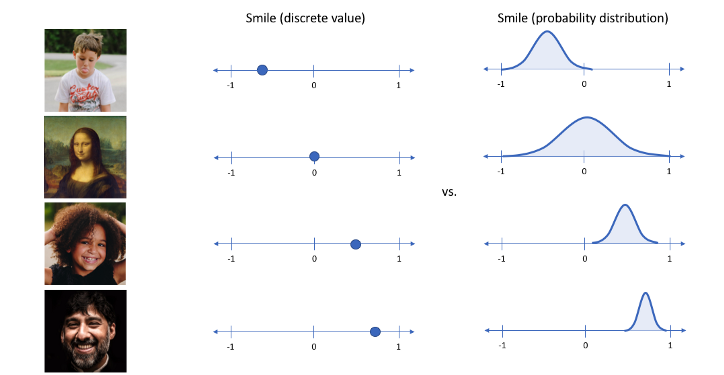

• input image가 들어오면 그 이미지의 다양한 특징들이 각각의 확률변수가 되는 확률분포를 만든다. 이 확률 분포를 잘 찾아내어 확률값이 높은 부분을 사용하면 그럴듯한 새로운 이미지를 생성할 수 있다.

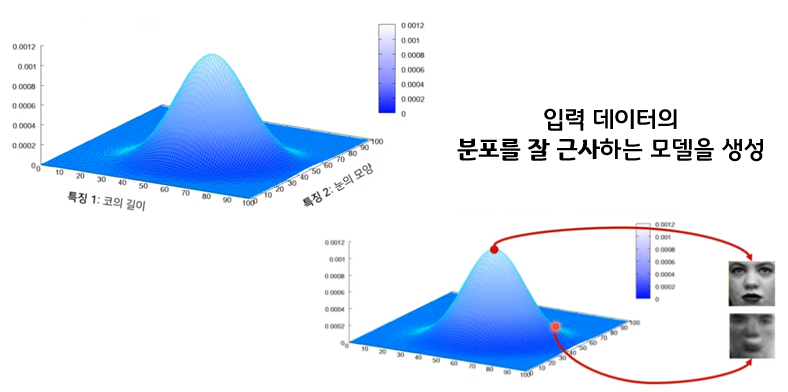
• 이때 각 feature가 가우시안 분포를 따른다고 가정하고 latent $z$는각 feature의 평균과 분산값을 나타낸다.

• 예를 들어 한국인의 얼굴을 그리기 위해 눈, 코, 입 등의 feature를 Latent vector $z$에 담고, 그 $z$를 이용해 그럴듯한 한국인의 얼굴을 그려내는 것이다. latent vector $z$는 한국인 눈 모양의 평균 및 분산, 한국인 코 길이의 평균 및 분산, 한국인 머리카락 길이의 평균 및 분산 등등의 정보를 담고 있다고 생각할 수 있다.

✅️ 수학적 의미

모델의 파라미터 $\theta$가 주어졌을 때, 우리가 원하는 정답인 $x$가 나올 확률 $p_{\theta*}(x)$가 높을 수록 좋은 모델이다. 따라서 $p_{\theta*}(x)$를 최대화하도록 파라미터를 학습시킨다.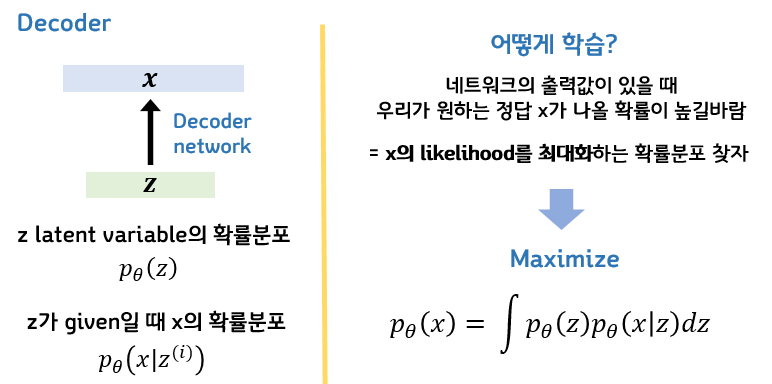

4.3) Variational Autoencoders

과정을 자세히 들여다보자.

• image가 들어왔을 때 $p(z)$는 image의 각 pixel에 대해 알맞는 각각의 가우시안 distribution이다.
• 즉, pixel별로 각각의 $\mu, \sigma$를 가진 가우시안 distribution을 갖는다.

그러나 만약 high resolution image라면 이는 매우매우매우 많은 값을 가질 것이다.
따라서 general Gaussian distribution 대신에 Diagonal Gaussian distribution을 사용한다. 즉, $z$가 주어졌을 때 generated image의 pixel들 사이의 covariance는 없다. pixel들은 independent하다.

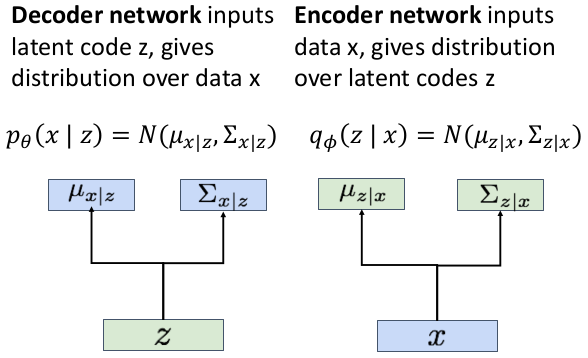
Decoder은 $z$를 입력받아서 mean $\mu_{x|z}$와 diagonal covariance $\sum_{x|z}$를 출력한다.
그리고 $\mu_{x|z}$, $\sum_{x|z}$를 갖는 Gaussian으로부터 $x$를 sample한다.

✅️ How to train this model?

maximize likelihood of data $p_{\theta*}(x)$

만약 우리가 $x$에 대해 $z$를 관측할 수 있다면 conditional generative model $p(x|z)$를 학습할 수 있을 것이다. 그러나 $z$를 관측할 수 없으므로 marginalize한다.

• $p_\theta(x|z)$는 decoder network의 output이므로 계산가능하다.
• $p_\theta(z)$는 우리가 정한 가우시안 prior이다.
• 그러나 모든 $z$에 대해 적분하는 것은 불가능하다.

따라서 베이즈 정리를 사용한다

• $p_\theta(x|z)$와 $p_\theta(z)$는 계산가능하다.
• 그러나 $p_\theta(z|x)$는 계산할 방도가 없다. (어떻게 생성하지도 않은 image가 주어짐을 가정할 수 있나.)

따라서 또다른 network(encoder) $q$를 도입한다.

새로운 네트워크 encoder은 위의 식을 학습한다.

따라서

위의 사실들을 조합하여 $p_\theta(x)$를 근사할 수 있다. 아래는 그 과정인데 이 식을 도저히 이해하기가 너무 힘들다. 언젠가 이해할 날을 기대하며 적어본다.

We can wrap in an expectation since it doesn't depend on z

마지막 식에서

• 첫번째 term : Data reconstruction
• 두번째 term : KL divergence between prior, and samples from the encoder network
• 세번째 term : KL divergence between encoder and posterior of decoder

그러나 세번째 term은 구할 수 없음. 하지만 KL은 항상 양수의 값을 가지므로 이는 likelihood의 lower bound를 구할 수 있게 해준다.

$\log p_\theta(x) \ge E_{z\sim q_\phi(z|x)}[\log p_\theta(x|z)] - D_{KL}(q_\phi(z|x),p(z))$

이를 통해 encoder과 decoder를 jointly하게 학습시켜서 data likelihood의 variational lower bound를 최대화시키는 방향으로 학습시킨다.

---

진자 VAE는 너무 이해하기가 힘들었고 공부하기도 힘들었다. 19강 강의 하나 보는데 6시간은 걸린 것 같다.. 그런데도 아직 정확히 이해하지 못한 것 같아서 좀 자괴감이 온다....