R-squared & Adjusted R square
R-squared
Adjusted R square
- 설명력이 없는 변수를 추가해도 R-square는 계속 증가하는 문제 보정
- SSE와 SST를 각각의 자유도로 나누어 줌
RMSE
-
Root Mean Square Error
-
편차의 제곱의 평균에 루트를 씌운 값
-
표본평균과의 비교를 통해 대략적인 모델 간 정확도를 비교할 수 있음.
-
표본평균이 100이고 RMSE가 10일 때 예측값이 표본평균 대비 10%의 변동성을 가진다고 해석.
-
예측값의 스케일에 영향을 받음. 종속변수의 단위가 커지면 RMSE도 커짐 ➡ 모델 간 정확도 비교할 때 표본 데이터가 다르면 RMSE 절대치로 비교를 해서는 안 됨.
ex) 평균 판매 갯수가 1천개인 a매장의 판매 갯수 예측값에 대한 RMSE와 평균판매갯수가 5천개인 B매장의 판매 갯수 예측값에 대한 RMSE는 스케일 자체가 다르기 때문에 예측력의 좋고 나쁨을 비교할 수 없다. -
절대적인 전체 오차 크기보다 실제값과 예측값의 오차가 들쑥날쑥하지 않은 모델을 더 우수하게 평가하는 특성
-
오차값을 제곱해 주기 때문에 MAE보다 이상치에 더 민감함.
MAE
- Mean Absolute Error
- '오차의 합의 평균' 개념으로 이해하면 쉽다.

⭐RMSE vs MAE
RMSE : 모델 예측 안정성 (오차가 들쭉날쭉하지 않는 것)
MAE : 절대적인 전체 오차 크기가 작은 것이 우수하게 평가
MAPE
- Mean Absolute Percentage Error
- MAE를 퍼센트로 변환한 것
- 스케일에 관계없이 절대적인 차이 비교 가능하여 모델 간 성능을 비교하기에 유용
- 0부터 무한대의 값을 가질 수 있음
- MAE랑 같은 예제 값에 대해 평가지표를 MAPE라고 가정했을 때 다음과 같이 정리할 수 있다.
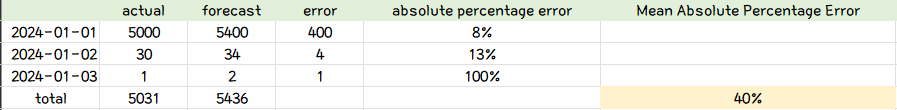
⭐주의
- 실제값()이 0인 경우에는 0으로 나눌 수 없기 때문에 MAPE를 구할 수 없음.
- 실젯값에 0이 많은 데이터는 MAPE 평가 기준을 사용하는 것이 적합하지 않음.
- 🔍하지만 실무에서 실제값이 0인 경우도 분명 발생한다. 이 경우 WMAPE로 평가지표를 두는 것을 고려할 수 있다.
- 실젯값이 양수인 경우, 실제값보다 작은 값으로 예측하는 경우 MAPE의 최댓값이 최대 100%r까지만 커질 수 있음. 반면 실젯값보다 크게 예측하는 경우 MAPE값이 한계가 없기 때문에 MAPE 기준으로 모델을 학습하면 실젯값보다 작은 값으로 예측하도록 편향될 수 있음
- 실제값이 0과 가까운 매우 작은 값인 경우 MAPE가 과도하게 높아지는 경우가 발생할 수 있다. EX) 실제값이 1이고 예측값이 5이면 MAPE는 400%가 됨.
정리
- 성능평가 방법을 선정하기 전에, 실제값과 예측값의 분포를 확인하고 이런 주의점들을 고려해 가장 적합한 방법을 선택하는 것이 중요하다.
