이번 포스팅에서는 수요예측 실무에서 오차율 지표로 자주 사용하는 MAPE에 대해 먼저 이해하고 실무에서 MAPE 대신 자주 사용하는 오차율 지표인 WMAPE에 대해 집중정리해보겠다.👀
Chap1.MAPE 이해하기
- Mean Absolute Percentage Error
- MAE를 퍼센트로 변환한 것
- 스케일에 관계없이 절대적인 차이 비교 가능하여 모델 간 성능을 비교하기에 유용
- 0부터 무한대의 값을 가질 수 있음
- MAE랑 같은 예제 값에 대해 평가지표를 MAPE라고 가정했을 때 다음과 같이 정리할 수 있다.
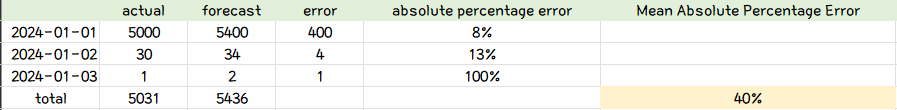
⭐주의
- 실제값()이 0인 경우에는 0으로 나눌 수 없기 때문에 MAPE를 구할 수 없음.
- 실젯값에 0이 많은 데이터는 MAPE 평가 기준을 사용하는 것이 적합하지 않음.
- 🔍하지만 실무에서 실제값이 0인 경우도 분명 발생한다. 이 경우 WMAPE로 평가지표를 두는 것을 고려할 수 있다.
- 실젯값이 양수인 경우, 실제값보다 작은 값으로 예측하는 경우 MAPE의 최댓값이 최대 100%r까지만 커질 수 있음. 반면 실젯값보다 크게 예측하는 경우 MAPE값이 한계가 없기 때문에 MAPE 기준으로 모델을 학습하면 실젯값보다 작은 값으로 예측하도록 편향될 수 있음
- 실제값이 0과 가까운 매우 작은 값인 경우 MAPE가 과도하게 높아지는 경우가 발생할 수 있다. EX) 실제값이 1이고 예측값이 5이면 MAPE는 400%가 됨.
Chap2. MAPE의 한계
- MAPE의 큰 단점은 실제값이 0인 경우 값을 산출할 수 없다는 점이다.
- 또한 매장별, 품목별 오차율을 각각 구한 뒤 전체 오차율을 산정할 때 단순 평균으로 구하는 것보다 규모에 따라 가중치를 차등 분배하여 산출하는 접근이 필요하다.
EX) 매장 A,B가 있을 때 매출 비중이 80:20이라면 매장 A에 더 높은 가중치를 두어 신경 쓸 필요가 있는 것이다.
MAPE의 이러한 단점을 보완해줄 지표가 WMAPE이다.
Chap3. WMAPE 개념
- weighted mean absolute error
- WMAPE의 경우 분모가 실제값의 합이므로 분모가 0이 되어 산출불가한 문제를 해결할 수 있다. (물론 이 경우에도 실제값의 합이 0이 되는 경우는 산출이 안되겠지만, 상식적으로 실제값을 합했는데도 모두 0이 되는거라면 애초에 예측을 하는 이유가 없기 때문에 논외로 하자!)

예시를 통해 쉽게 이해해보자!

- C매장의 경우 실제값이 0이라 (M)APE 식에서는 에러가 발생하지만 W(M)APE식에서는 정상 산출이 된다.
- A매장과 B매장을 비교했을 때 B매장의 오차율이 더 크긴하지만 절대적인 값의 단위는 A매장이 크다. 이에 WMAPE로 산출했을 때 이러한 중요도차이(가중치 차이)를 고려한 결과값을 얻을 수 있다.
- 좀 더 단순하게 접근해보자면 "오차의 합/실제값의 합" 으로 이해할 수 있겠다

Chap4. 실무 관점에서 해석하기
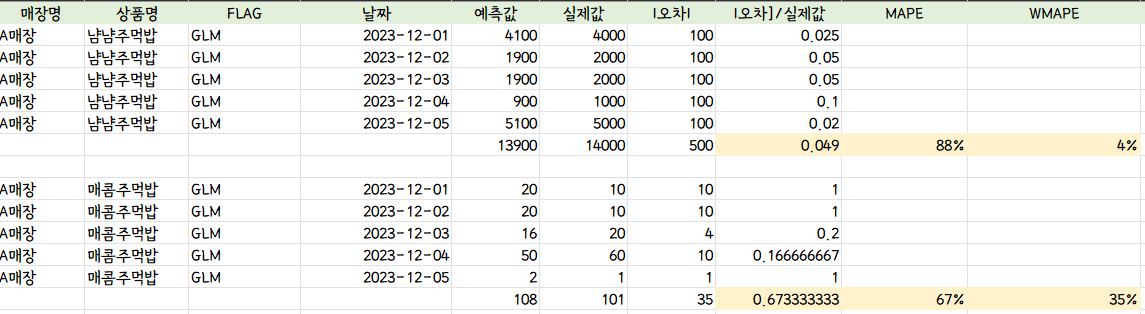
1) 품목별 오차율 비교
- MAPE 기준으로는 냠냠주먹밥의 오차율이 높지만 WMAPE를 기준으로 생각했을 때에는 매콤주먹밥의 오차율이 높다.
⭐⭐⭐ 따라서 오차율이 낮으니 예측을 잘하고 있다고 단순하게 결론짓기보다는 평가 지표에 따라 해석할 수 있는 안목을 기르는 것이 중요하다.
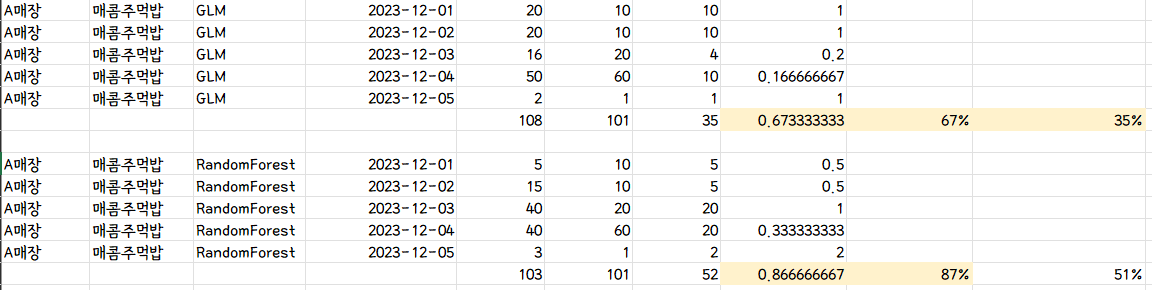
2) 알고리즘별 비교
- 같은 매장, 상품에 대해 알고리즘별로 성능테스트를 할 때 다음과 같이 사용할 수 있다.
Reference
3개의 댓글
https://www.globhy.com/article/buying-horizontal-carbonized-bamboo-flooring-from-china-while-living-in-new-york
https://www.globhy.com/article/why-bamboo-flooring-is-the-eco-friendly-champion-of-sustainable-homes
https://www.hentai-foundry.com/user/bothbest/blogs/20350/Choosing-Bamboo-Flooring-for-My-London-Home
https://yamap.com/users/4784209
https://forum.iscev2024.ca/member.php?action=profile&uid=1357
https://my.usaflag.org/members/bothbest/profile/
https://myliveroom.com/bothbest
https://forum.geckos.ink/member.php?action=profile&uid=642
https://competitorcalendar.com/members/bothbest/profile/
https://www.fruitpickingjobs.com.au/forums/users/bothbest/
https://thefwa.com/profiles/bamboo-flooring
https://chanylib.ru/ru/forum/user/9508/
https://greenteam.app/bothbest
http://www.v0795.com/home.php?mod=space&uid=2304271
https://wearedevs.net/profile?uid=201358
https://www.templepurohit.com/forums/users/chinahousehold/
https://tutorialslink.com/member/FlooringBamboo/68089
https://www.tkaraoke.com/forums/profile/bothbest/
https://www.aipictors.com/users/bothbest
https://forum.index.hu/User/UserDescription?u=2129081
http://programujte.com/profil/75582-chinabamboo/
https://lamsn.com/home.php?mod=space&uid=1290622
https://nexusstem.co.uk/community/profile/chinabamboo/
https://brain-market.com/u/chinabamboo
https://malt-orden.info/userinfo.php?uid=414587
https://www.halaltrip.com/user/profile/255692/chinabamboo/
https://goodgame.ru/user/1698091
https://vcook.jp/users/42177
https://library.zortrax.com/members/china-bamboo/
https://aprenderfotografia.online/usuarios/chinabamboo/profile/
https://plaza.rakuten.co.jp/chinabamboo/
https://plaza.rakuten.co.jp/chinabamboo/diary/202508270000/
https://plaza.rakuten.co.jp/chinabamboo/diary/202508270001/
https://eternagame.org/players/538402
https://www.slmath.org/people/82724
https://www.aipictors.com/users/chinabambooflooring
https://vocal.media/authors/china-bamboo-bfc
https://www.giantbomb.com/profile/chinabamboo/
https://www.keedkean.com/member/44724.html?type=profile


안녕하세요, MAPE 계산식에서 40%가 어떻게 도출 되었는지 알수 있을까요? 8% 13% 10%의 합인 31%를 3으로 나눈다고 생각했는데, 결과가 달라서 문의 드립니다 :)