2학기 알고리즘 때 제대로 배운 (ㅎㅎ) 다이내믹 프로그래밍을 연습해보려고한다.
PS는 앞으로 겨울방학 기간 동안에 계속 최소 하루에 한 문제씩 풀기.
부지런하게 살아보려한다.
첫 번째 날, 첫 번째 PS
9095번: 1, 2, 3 더하기
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.
1+1+1+1
1+1+2
1+2+1
2+1+1
2+2
1+3
3+1
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.
n을 1, 2, 3의 조합으로 나타내는 문제이다.
간단하게 4까지의 가짓수를 찾아보았는데
1 = 1
2 = 1+1, 2
3 = 1+1+1, 1+2, 2+1, 3
4 = 1+1+1+1, 1+1+2, 1+2+1, 2+1+1, 1+3, 3+1, 2+2
1, 2, 3까지는 별다른 규칙이 안보이지만, 4에서부터 1, 2, 3 가짓수가 보였다.
예를 들어, 1+1+1+1은 3의 가짓수 중 하나인 1+1+1에 1을 더하면되고
1+1+2는 2의 1+1에 2를 더하며된다.
즉 4라는 가짓수는 1 가짓수 + 3, 2 가짓수 + 2, 3 가짓수 + 1이다.
여기서 점화식을 세우면
다음과 같이 작성할 수 있다.
아래는 코드이다.
// 백준 9095번 문제 / DP
#include <iostream>
using namespace std;
int func(int, int, int);
int main(void) {
int T = 0, n = 0, a[12] = {0};
cin >> T;
a[1] = 1, a[2] = 2, a[3] = 4;
for(int i=4;i<12;i++) {
a[i] = a[i-1] + a[i-2] + a[i-3];
}
for(int i=1;i<=T;i++) {
cin >> n;
cout << a[n] << endl;
}
return 0;
}점화식을 이용해서 혼자서 직접 풀어보았는데 처음 연습해보기에 적당한 것 같다.
굳이 헷갈렸던 점을 꼽자면 순열에 집착한 나머지 앞선 세가지의 가짓수에 포함된다는 것을 까먹고 가짓수에 값을 더하고 순서를 고려해야하는 줄 알고 잠깐 혼란스러웠다
다음 문제,
백준 1010번: 다리 놓기
문제

N개의 다리를 겹치지 않고 둘 수 있는 가짓수를 구하여라 ~ 문제이다.
문제를 보면은 뭔가 조합으로 풀어도 풀릴 것 같았는데, 난 DP 문제를 연습해보기로 했으니까 DP로 풀이해보려고한다. 내 방법이 조금 무식할 수는 있어도 내가 생각해난 방법은 이거밖에 ㅠㅠㅠ
그래서 다른 방법으로 접근을 해보았다.
만약 N=2, M=4라 가정해보자.
이때 강 서쪽의 첫 번째 다리를 동쪽의 첫 번째랑 연결하면은
N=1, M=3이 가짓수가 되고
서쪽의 첫 번째 다리를 동쪽의 두 번째 다리랑 연결하면은
N=1, M=2이 가짓수가 되고
동쪽의 세 번째 다리랑 연결하면은
N=1, M=1이 가짓수가 된다.
즉, N=2, M=4의 가짓수는 (N=1, M=3) + (N=1, M=2) + (N=1, M=1)의 합이다.
N=A, M=B의 가짓수는 (N=A-1, M=B-1), (N=A-1, M=B-2), (N=A-1, M=B-3) .. M이 1이 될 때까지의 합이다.
위 내용을 표로 그려보면 더 눈에 띄는 규칙성(?)을 확인할 수 있다.
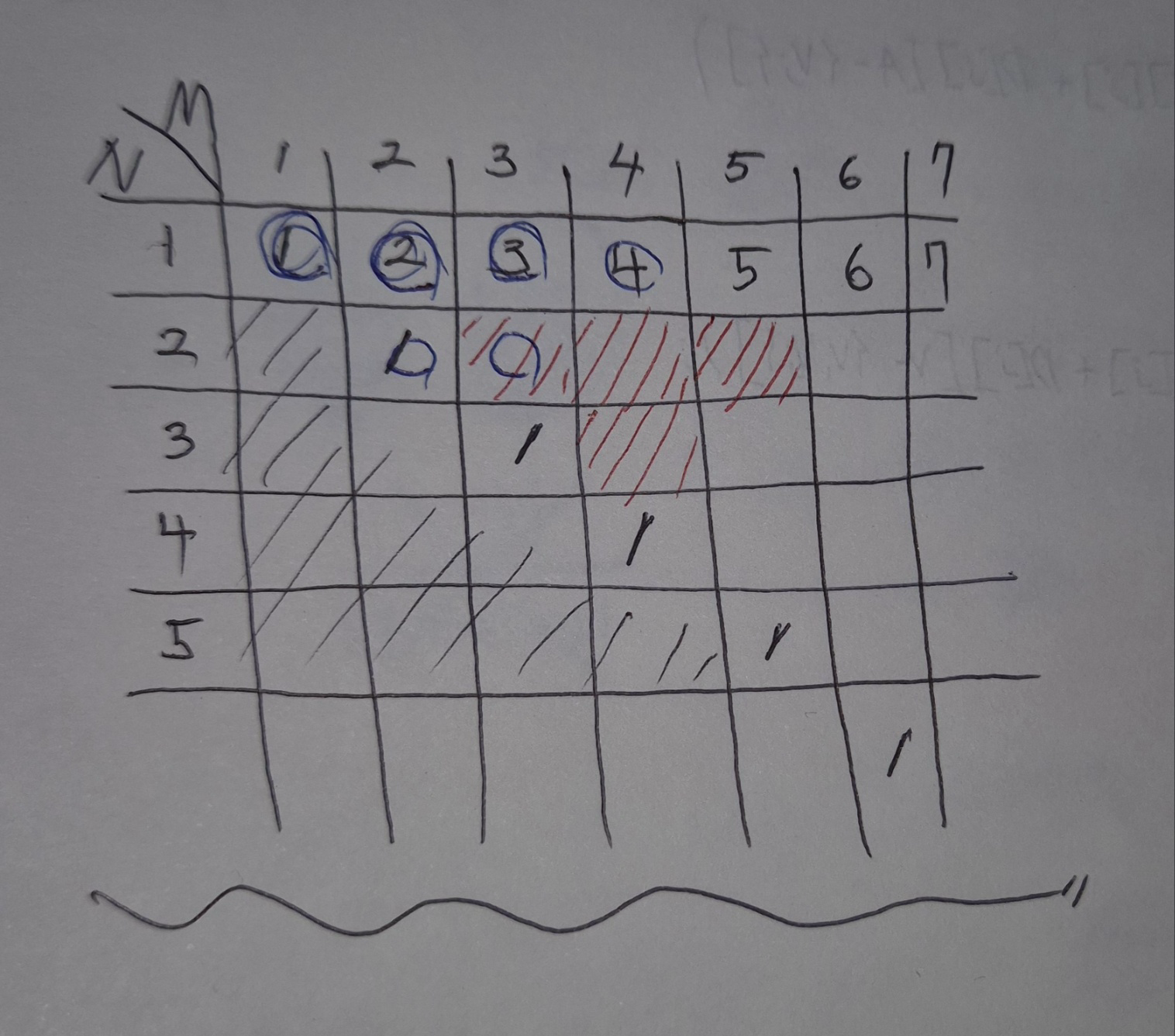
ㅋㅋ 내가 이해하면서 그려본 그림인데, 다른 사람은 이해못할 것 같당
여튼, 내가 생각해본 방식으로 코드를 짜보겠다.
#include <iostream>
using namespace std;
int main(void) {
int T = 0, N = 0, M = 0;
int DP[31][31] = {0};
for(int i=1;i<=30;i++) { // 초기화
DP[i][i] = 1;
DP[1][i] = i;
}
for(int i=2;i<=30;i++) { // row
for(int j=i+1;j<=30;j++) { // col
for(int k=1;k<=j-1;k++) {
DP[i][j] += DP[i-1][k];
}
}
}
cin >> T;
for(int i=0;i<T;i++) {
cin >> N >> M;
cout << DP[N][M] << endl;
}
return 0;
}우선 1행이랑 대각행렬에 대하여 초기화를 해주고
초기화 값을 기반으로
값을 계산하면 된다. 위 코드에서는 DP라는 2차원 배열로 구하였다.

풀어서 기분은 좋지만, 만약 30개가 아닌 수백, 수천개, n개가 들어온다면은
시간복잡도는 n^3인건가 ? 쩝 아쉽구만
