20일은 백준만 풀고, 일정이 있어 따로 블로그 글은 작성하지 않았다.
최대한 이런 경우가 없도록 하겠음
오늘의 DP 문제는
2839: 설탕 배달
주어진 N값은 3과 5로 표현을 할 때, 최소의 갯수로 표현하는 알고리즘을 구현하는 것이 목표이다.
3 => 1
6 => 2
9 => 3
15 => 3 (5 + 5 + 5)
이런 식으로 표현하면 된다.
역시, A[3] = 1, A[5] = 1이라는 초기값을 이용해서 DP로 풀어보려한다 !
이전에 풀었던 문제들이랑 굉장히 비슷해서
algorithm 헤더파일의 min을 이용해서 풀었는데, 기존 다른 값들이 0으로 초기화되어있다는 것을 인지하지 않고 분기문을 제대로 작성하지 않아 버벅였다.
#include <iostream>
#include <algorithm>
using namespace std;
int main(void) {
int N, A[5001];
cin >> N;
A[3] = 1, A[5] = 1;
for(int i=6;i<=N;i++) {
if(A[i-3])
A[i] = A[i-3] + 1;
if(A[i-5])
A[i] = A[i] ? min(A[i], A[i-5] + 1) : A[i-5] + 1;
}
cout << (A[N] != 0 ? A[N] : -1) << endl;
return 0;
}DP 테이블 업데이트를 위해 해당 값이 0이 아닌지 판독하고 진행하면 깔끔하다 !
마찬가지로 두 번째 if문에서 A[i] 값을 고려하지 못해 조금 막혔었ㄷ다. 차분히 풀 수 있는 힘을 길러야겠다.
너무 간단한 문제만 푸는 것 같아 한 문제 더 풀어보았다 !
12865번: 평범한 배낭
Knapsack 알고리즘으로 유명한 배낭 문제이다.
용량을 넘지 않으면서 담을 수 있는 가치합의 최대를 구하는 문제인데
표를 그리지 않으면 이해하기 어려웠던 것 같다.
특히, 코드로 옮기는 과정에서 잘 안써본 pair를 이용해서 하다보니 많이 버벅였다 ㅠㅠ
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main(void) {
int N = 0, K = 0;
cin >> N >> K;
vector<pair<int, int> > T (N + 1); // W = first, V = second
vector<vector<int> > DP (N + 1);
for (int i = 0; i <= N; i++) {
DP[i] = vector<int>(K + 1, 0); // 각 행을 크기 K+1로 초기화
}
for(int i=1;i<=N;i++)
cin >> T[i].first >> T[i].second;
for(int i=1;i<=N;i++) {
for(int j=1;j<=K;j++) {
if(T[i].first > j) { // i번째 품목 추가할지 말지 결정.
DP[i][j] = DP[i - 1][j];
}
else {
DP[i][j] = max(DP[i - 1][j], DP[i - 1][j - T[i].first] + T[i].second);
}
}
}
cout << DP[N][K] << endl;
return 0;
}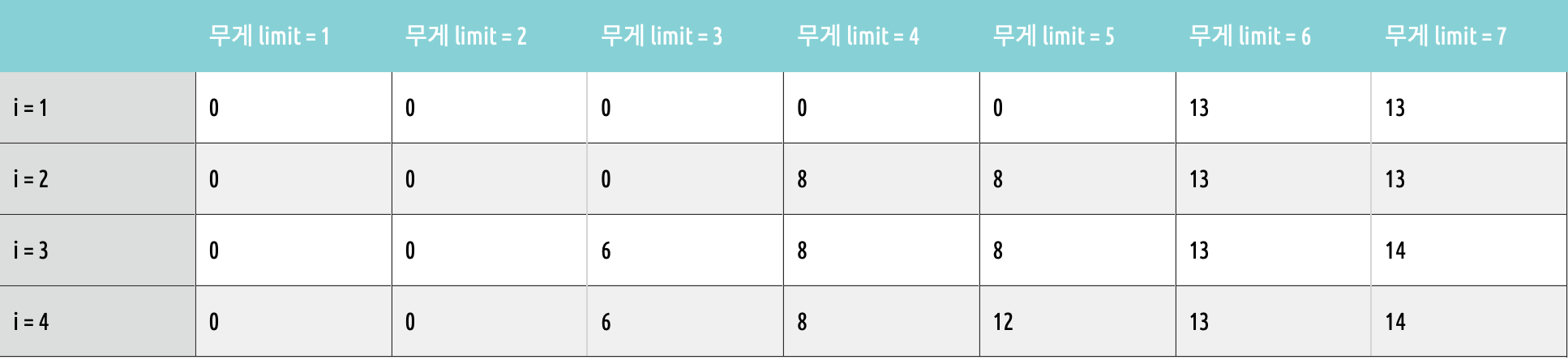
위 표는
https://nanyoungkim.tistory.com/182 이 선생님의 사이트에서 가져온 표인데 너무 잘 설명해주셔서 가져와봤다. 감사합니다
무게 제한을 걸어서 그 무게를 넘지않으면서 현재 물건을 담을 수 있는지 체크하고
만약 담을 수 없다면 그냥 같은 열, 이전 행의 값을 가져오면 되는 것이고
담을 수 있다면은 max(같은 열 이전 행의 값, 현재 물건의 무게를 제외한 최대 가치 + 현재 물건의 가치)를 저장하면 된다.
말로 설명하려다보니 어렵게 됐는데
수식으로 보는 것이 더 편할 듯하다.
P[i][j] 는 전체 무게 w가 넘지 않는 i번째 항목까지의 최대 항목이다.
더 연습이 필요할 듯 하다. 끝
