알바를 하느라 오랜만에 백준을 하게 되어서 이제야 글을 쓰게되었다.
정말 정신이 없어서 매일 하겠다는 약속을 벌써 깨버렸지만, 남은 기간 성실히 해보도록 하겠슴돠
오늘이 문제는
2156번: 포도주 시식
입니다.
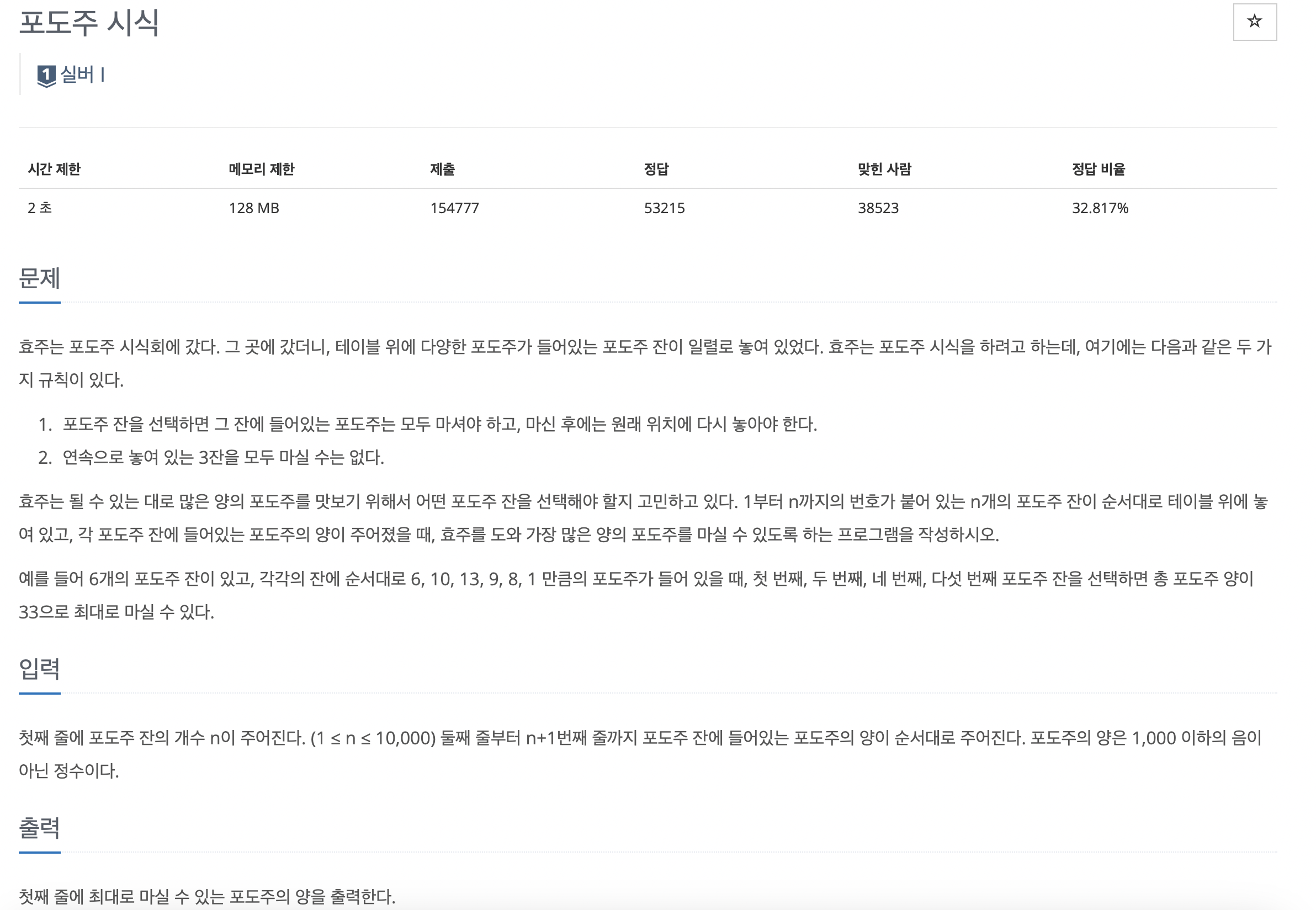
저번에 풀었던, 계단을 오를 수 있는 가장 큰 값을 출력해라 인가 그거랑 굉장히 비슷하다고 생각하였다. 연속 3개를 한 번에 선택할 수 없다는 점과 최대 값을 출력하라는 점이 결이 비슷한 문제라고 생각하여서 똑같이 접근을 해보았는데 잘 안풀렸다.
그 이유는 계단 문제는 결국 맨 마지막 계단을 무조건 밟아야하기 때문에 맨 마지막을 밟는 것을 기준으로 밟는 방식을 구분하여 문제를 풀이했지만, 여기는 맨 마지막 잔을 먹어도 되고, 안 먹어도 된다는 것을 간과했기 때문이다.
간단한 예시로 알 수 있다.
10 10 10 9 이런 식이면은 맨 마지막 잔, 9는 안 먹어야 최댓값을 가지기 때문이다.
계단 문제와 같다는 확신으로 접근하여서 이런 오류가 발생했던 것 같다.
그러면 어떻게 접근을 해야할까
똑같이 case를 구분해주면 된다.
만약, i번째 와인까지의 최댓값을 구한다고 가정해보자.
그러면 경우의 수는 크게 2가지, 세부적으로 총 3가지가 존재한다.
- i번째 와인을 마시는 경우
- i번째 와인을 마시지 않는 경우
맨 처음 1번 케이스에서
i번째 와인을 마시는 경우는 아래와 같이 구분해볼 수 있다.
1-a) i-1번, i번 와인을 연달아 마시는 경우
1-b) i-2번, i번 와인을 마시는 경우
식으로 나타내면은
1-a)
DP[i] = DP[i-3] + wine[i-1] + wine[i];
1-b)
DP[i] = DP[i-2] + wine[i];
2번 케이스에서는 i번째 와인을 마시지 않는 경우이므로
DP[i] = DP[i-1];
이다.
마시지 않는 경우가 이해되지 않을 수 있는데, 이전에 두 잔을 연속으로 마셨다면은 현재 잔을 마실 수 없기 때문에 고려하는 것이다.
3 2 1이면은 세번째 와인을 마시지 않고 나머지 두 와인을 마시는 것이 최대인 것을 생각하면은 이해가 빠르다.
그래서 위 점화식을 이용하여서 코드를 작성해보면
#include <iostream>
#include <algorithm>
using namespace std;
int main(void) {
int n, DP[10001] = {0}, alco[10001] = {0};
cin >> n;
for(int i=1;i<=n;i++) {
cin >> alco[i];
}
DP[1] = alco[1];
DP[2] = alco[1] + alco[2];
for(int i=3;i<=n;i++) {
DP[i] = max(DP[i - 3] + alco[i - 1], DP[i - 2]) + alco[i];
DP[i] = max(DP[i], DP[i - 1]);
}
cout << max(DP[n], DP[n - 1]) << endl;
return 0;
}이다.
사실은 다시 풀 때 한 번에 맞은 것이 아니라 그 현재 와인을 마시지 않는 경우를 고려하지 않아서 한 번 틀렸다 ㅎ
점화식을 분석할 때는 시간이 오래 걸려도 좋으니 신중하게 해야긋다.
끝.
앞으로도 계속 바빠서 백준을 못할 수도 있을텐데, 최대한 열심히 해보려고 하겠다.
