또 DP 풀기 DP 마스터 할때까지 풀 계획(질리면 넘어감)

1149 RGB 거리

#include <iostream>
#include <algorithm>
using namespace std;

int n ,street[1000][1000];
int cache[1000][1000];

int paint(int x, int c) {
	if (x == n - 1) return street[x][c];
	int& ret = cache[x][c];
	if (ret != 10000000) return ret;
	return ret = street[x][c] +
		(c == 0 ? min(paint(x + 1, 1), paint(x + 1, 2)) : (c == 1 ? min(paint(x + 1, 0), paint(x + 1, 2)) : min(paint(x + 1, 0), paint(x + 1, 1))));
}

int main() {
	cin >> n;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < 3; j++) {
			cin >> street[i][j];
			cache[i][j] = 10000000;
		}
	}
	cout << min({ paint(0, 0), paint(0, 1), paint(0, 2) });
	return 0;
}

좀 감이 생긴 것 같긴 하다.. 근데 멍청한 실수를 자꾸!!
paint에서 return할 때 x + 1이라고 적어야하는데 x++이라고 적어서 삽질했다..😥

📍 DP에서 까먹지 말아야 할 것

• 이전 값을 넘기지 않고 재귀
• 기저 사례 처리(처음엔 x == n-1에서도 최솟값을 넘기려고 했는데 그럴 필요가 전혀 없었다)
• 최솟값 구하는 경우면 memset(0 or -1) 불가능!

12865 평범한 배낭

#include <iostream>
#include <cstring>
using namespace std;

int n, full, items[100][2];
int cache[100001][101];

int pack(int remain, int t) {
	if (t == n) return 0;
	int& ret = cache[remain][t];
	if (ret != -1) return ret;
	ret = pack(remain, t + 1);
	if (remain >= items[t][0]) {
		return ret = max(pack(remain - items[t][0], t + 1) + items[t][1], ret);
	}
	return ret;
}

int main() {
	memset(cache, -1, sizeof(cache));
	cin >> n >> full;

	for (int i = 0; i < n; i++) {
		for (int j = 0; j < 2; j++) {
			cin >> items[i][j];
		}
	}
	cout << pack(full, 0);
	return 0;
}

cache[남은 무게][n번째 물건] 으로 하는건 책의 힌트를 봤다. 사실 거의 이런 식이었긴 했는데 저렇게 하면 남는 부분이 많이 생기니까 아닐거라고 생각했던 것 같다.

아직 남은 무게가 현재 물건의 무게보다 큰 경우는 넣거나 말거나 중 더 큰 것 return, 남은 무게가 현재 물건의 무게보다 작은 경우는 안 넣는 것만 return

9251 LCS

#include <iostream>
#include <cstring>
using namespace std;

string s1, s2;
int s1l, s2l;
int cache[1001][1001];

int LCS(int m, int n) {
	if (m == s1.length() || n == s2.length()) return 0;
	int& ret = cache[m][n];
	if (ret != 0) return ret;
	ret = LCS(m + 1, n);
	for (int i = m; i < s1.length(); i++) {
		for (int j = n; j < s2.length(); j++) {
			if (s1[i] == s2[j]) {
				return ret = max(LCS(i + 1, j + 1) + 1, ret);
			}
		}
	}
	return ret;
}

int main() {
	memset(cache, 0, sizeof(cache));
	cin >> s1 >> s2;
	cout << LCS(0, 0);
	return 0;
}

94%에서 시간 초과가 떴다.

ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);

을 추가해도 시간초과, 0으로 초기화니까 memset(cache, 0, sizeof(cache)); 가 필요없음을 깨달아서 지워도 시간초과!

원인이 이중 for문인 것 같아서 for문을 없애는 방향으로 변경했다.

#include <iostream>
#include <cstring>
using namespace std;

string s1, s2;
int cache[1001][1001];

int LCS(int m, int n) {
	if (m == s1.size() || n == s2.size()) return 0;
	int& ret = cache[m][n];
	if (ret != -1) return ret;
	if (s1[m] == s2[n]) return ret = max(LCS(m + 1, n + 1) + 1, LCS(m + 1, n));
	else return ret = max(LCS(m + 1, n), LCS(m, n + 1));
}

int main() {
	memset(cache, -1, sizeof(cache));
	cin >> s1 >> s2;
	cout << LCS(0, 0);
	return 0;
}

잘 보면 cahce를 -1로 초기화하는 코드도 다시 돌아왔다. 왜냐.. 어차피 기저 사례의 return 0 때문에 사용하는 cache는 0으로 초기화 되고, 그래서! if(ret != 0) 에 걸리지 않는다... 또 시간 초과의 무한 굴레

DP는 정말 for문 없이 풀 수 있는거구나..🤨

11052 카드 구매하기

#include <iostream>
using namespace std;

int n, card[1001];
int cache[1002][1002];

int buy(int cnt, int c) {
	if (cnt > n || c > n) return 0;
	int& ret = cache[cnt][c];
	if (ret != 0) return ret;
	if (cnt + c <= n) return ret = max(buy(cnt + c, c) + card[c], buy(cnt, c + 1));
	return ret;
}

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> card[i];
	}
	cout << buy(0, 1);
	return 0;
}

cache[현재 카드 개수][현재 카드 번호] 로 설정했다. 카드 중복이 가능하므로 카드 개수가 넘지 않는 경우 사거나 말거나 중 더 큰 걸로 return하면 된다.

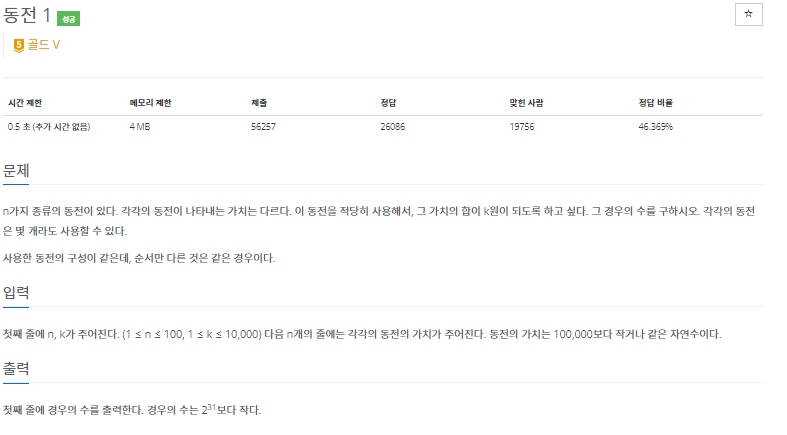
2293 동전 1

#include <iostream>
using namespace std;

int n, price;
int coin[101];
int cache[10001];

int pay(int now) {
	cache[0] = 1;
	for (int i = 0; i < n; i++) {
		for (int j = coin[i]; j <= price; j++) {
			cache[j] += cache[j - coin[i]];
		}
	}
	return cache[price];
}

int main() {
	cin >> n >> price;
	for (int i = 0; i < n; i++) {
		cin >> coin[i];
	}
	cout << pay(price);
}

경우의 수 구하기라 앞서 풀었던 문제들이랑 조금 달랐다.
1원을 써서 1~10원 만들기, 2원을 써서 2~10원 만들기… 이런 식으로 나가면 된다.